A string of length 0.4m and mass 10−2kg is tightly clamped at its ends. The tension in the string is 1.6N. Identical wave pulse are produced at one end at equal intervals of time, Δt. The minimum value of Δt which allows constructive interference of successive pulse is
0.05 s
0.40 s
0.20 s
0.10 s
The correct Answer is:d
The speed of transverse wave in a flexible stretched
string depends upon the tension T in the string and the
mass per unit length (μ) as
v=√Tμ=√Tm/l
Putting the numerical values form the question,
∴v=√1.610−2/0.4=8 ms−1
We know that when pulse is reflected from the other end
it suffers a phase change of 180∘. Again when the
reflection takes place from first end, a phase change of
180∘ occurs. Therefore, after successive reflections same
wavve pulse is obtained as previous. If at this instant
another same wave pulse is obtained, then these two
wave pulses produce constructive interference.
Hence, for constructive interference between successive
pulses Δtmin=0.4+0.48=0.10 s
Topper's Solved these Questions
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - EXERCISE 2
27 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- SEMICONDUCTORSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEMICONDUCTORSEXERCISE - MHT CET Corner
25 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
Similar Questions
A string of length 20 cm and linear mass density 0.40gcm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an end as shown in figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again ? (b) Sketch the shape of the string at a time half of that found in part (a).

View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N.A wave pulse is produced at t=0 near an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? (in ×10−2s)
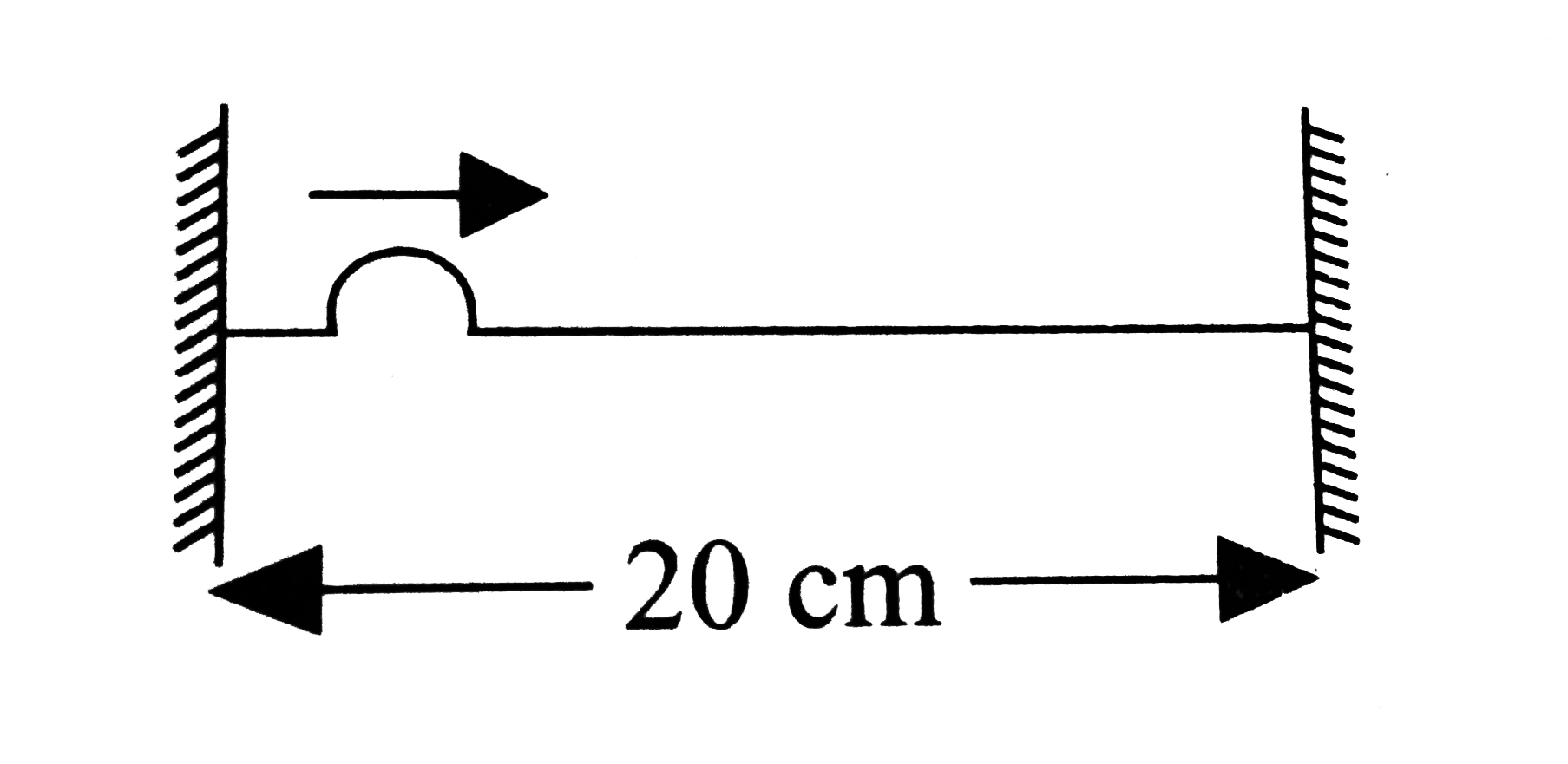
View Solution
Knowledge Check
A string of length 0.4m and mass 10−2kg is tightly clamped at its ends. The tension in the dtring is 1.6N. Idential wave pulse are produced at one end at equal intervals of time, Δt. The minimum value of Δt which allows constructive inetrference successive pulse is
A(a) 0.04sB(b)0.10sC( c ) 0.20sD(d) 0.40sA string of length 0.4m and mass 10−2kg is clamped at one end . The tension in the string is 1.6N. The identical wave pulses are generated at the free end after regular interval of time , Δt . The minimum value of Δt , so that a constructive interference takes place between successive pulses is
A0.1sB0.05sC0.2sDconstructive interference cannot take placeA string of length 0.4 m and mass 10−2 kg is clamped at its ends. The tension in the string is 1.6 N. When a pulse travels along the string the shape of the string is found to be the same at times t and t+△t. The value △t is
A0.05sB0.1sC0.2sD0.4s
A string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N . A wave pulse is produced at t=0 near an ends as shown in Fig. 7.17 (b) , which travels towards the other end . When will the string have the shape shown in the Fig . ( c).
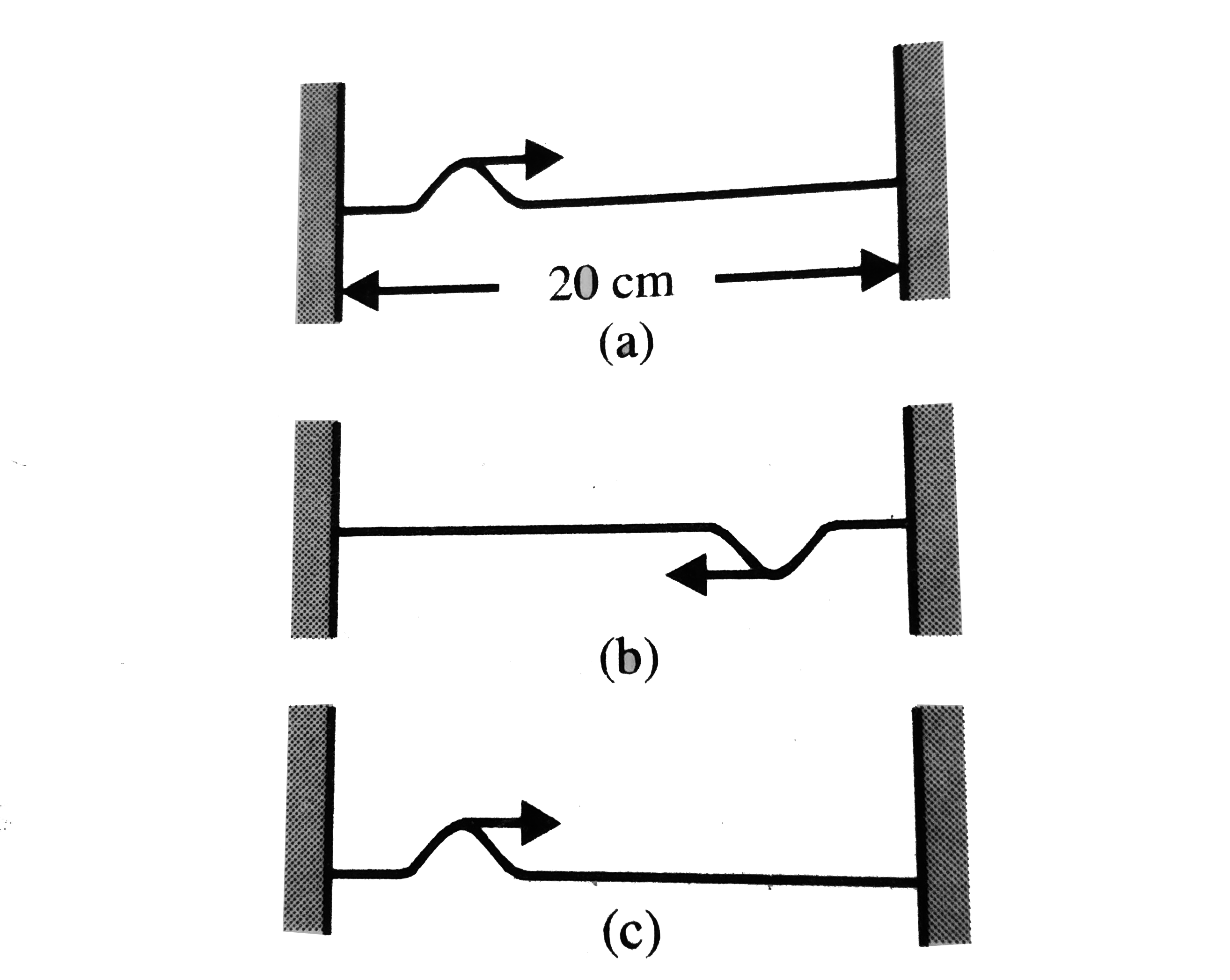
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA string of length 10.0 m and mass 1.25kg stretched with a tension of 50N. If a transverse pulse is created at one end of the string, how long does it take to reach the other end ?
View SolutionA string of mass per unit length μ=6×10−3 kg/m is fixed at both ends under the tension 540 N. If the string is in resonance with consecutive frequencies 420 Hz and 490 Hz. Then find the length of the string?
View Solution
