Question

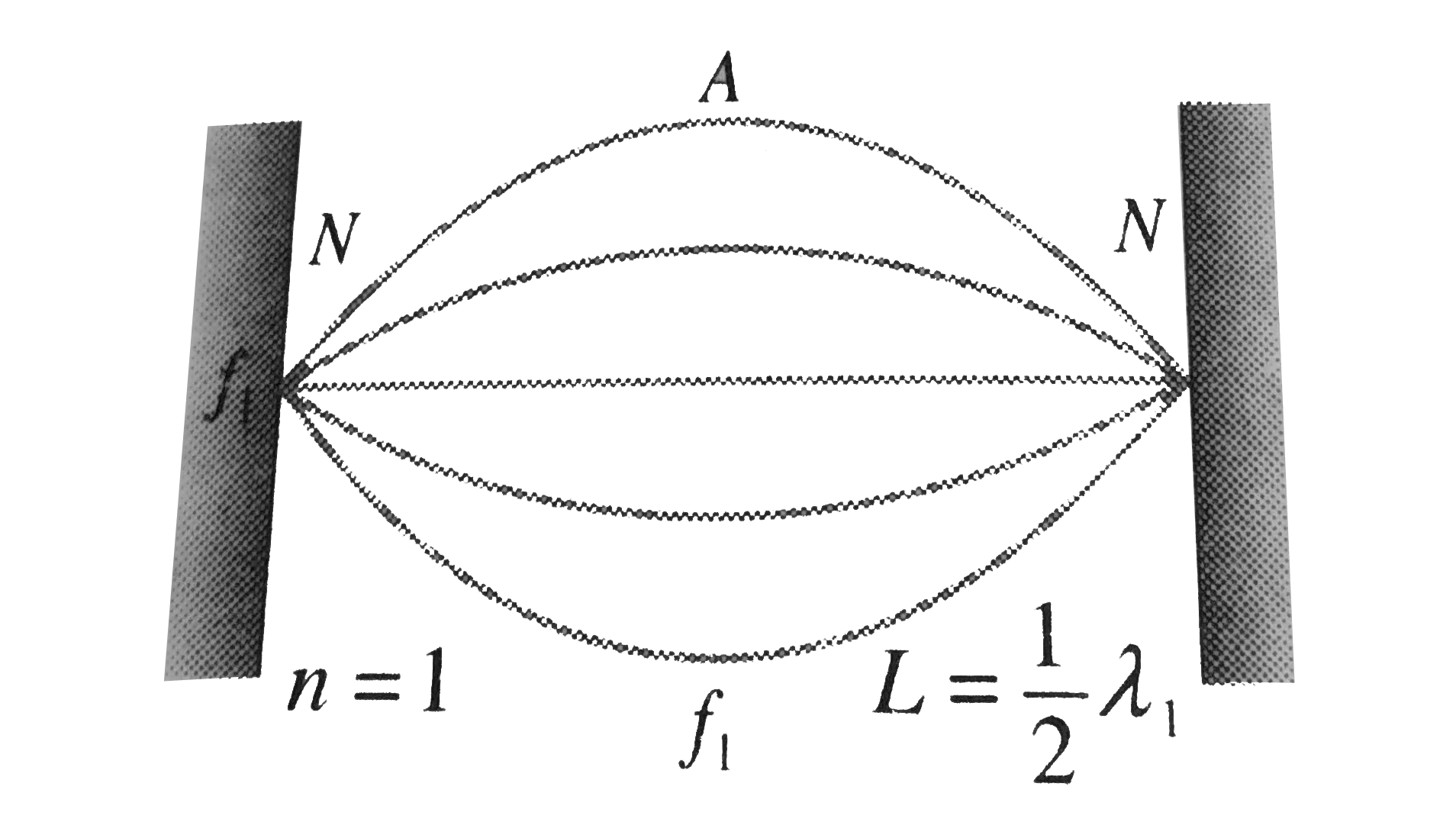
A string vibrates in its first normal mode with a frequency of $220$ vibrations $/s$. The vibrating segment is $70.0cm$ long and has a mass of $1.20g$.
(a) Find the tension in the string.
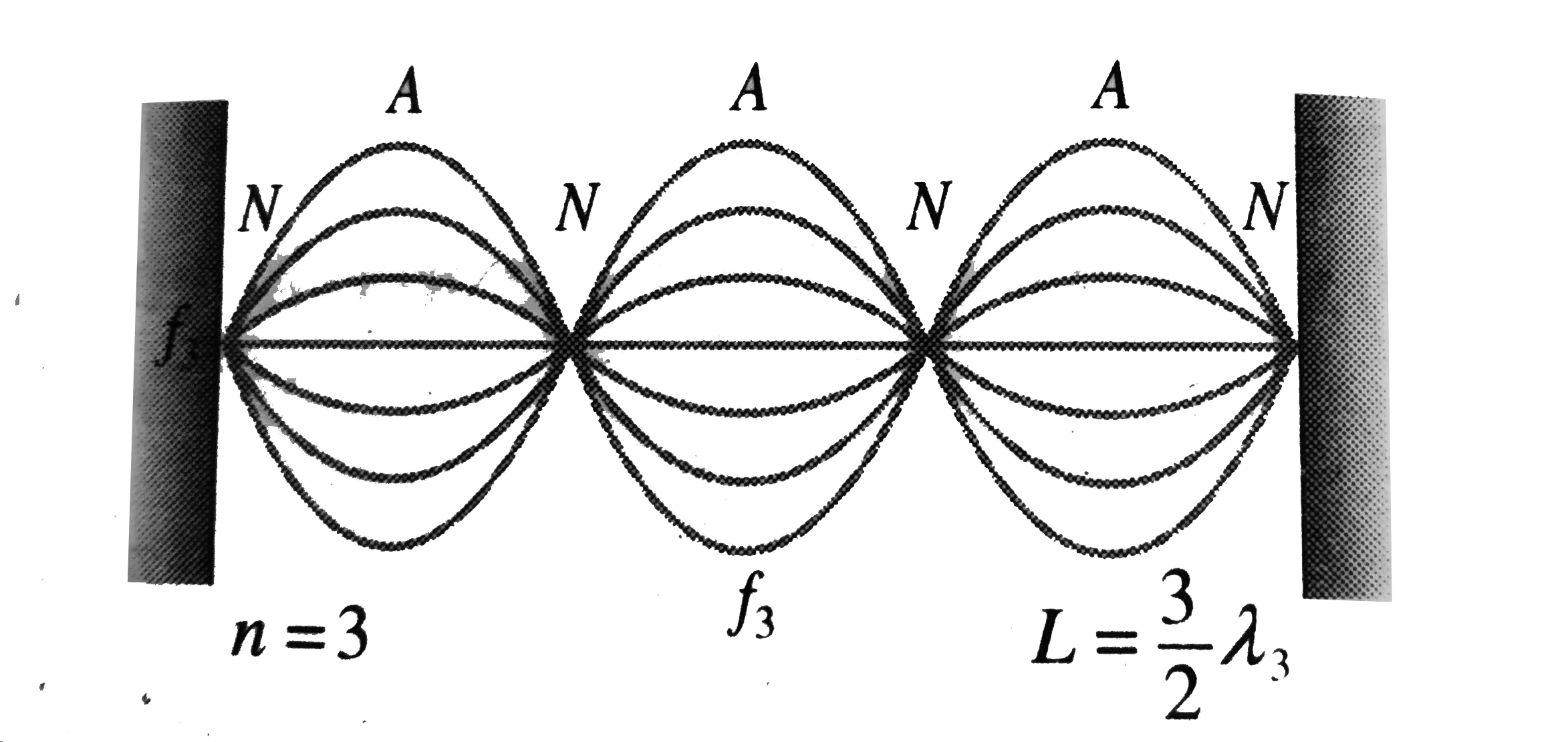
(b) Determine the frequency of vibration when the string vibrates in three segments.

Explanation

The tension should be less than ` 500 N (~ 100 1b)` since excessive force on the four cello strings would break the neck of the instrument . If a string vibrates in three antinodes ( instead of one for the fundamental mode) , so the frequency should be three times grreater than the fundamental .
From the string's length , we can find the wavelength . We then can use the wavelength with the fundamental frequency to find the wavr speed . Finally , we can find the tension from the wave speed and the linear mass density of the string .
When the string vibrates in the lowest frequency mode , the length of string forms a standing wave where is ` L = lambda//2` so the fundamental harmonic wavelength is `lambda = 2 L = 2( 0.700 m)`
`= 1.40 m` and the speed is
` v = f lambda = ( 220 s^(-1)) ( 1.40 m) = 308 m//s`
(a) . From the tension equation
` v = sqrt ((T)/( mu)) = sqrt ((T)/( m//L))`
We get ` T = v^(2) m//L`
or `T = ((308 m//s)^(2) ( 1.20 xx 10^(-3) kg))/( 0.700 m) = 163 N`
(b). For the third harmonic , the tension , linear density and speed are the same , but the string vibrates in three segments . Thus , the wavelength is one - third of the fundamental wavelength .
` lambda_(3) = lambda_(1)//3`
From the equation ` v= f lambda` , we find that the frequency three times as high .
` f_(3) = (v)/( lambda_(3)) = 3(v)/( lambda_(1)) = 3 f_(1) = 660 Hz`
The tension seems reasonable , and the third harmonic is three times the fundamental frequency as excepted . Related to part (b) , some stringed instrument players use a technique to double the frequency of a note by playing a natural harmonic , in effect cutting a vibrating string in half . When the string is lightly touched at its midpoint to form a node there , the second harmonic is formed , and the resulting note is one octave higher ( twice the original fundamental frequency ).