A student focussed the image of a candle flame on a white screen using a convex lens. He noted down the position of the candle, screen and the lens as under
Position of candle
Position of convex lens
Position of the screen
(i) What is the focal length of the convex lens ?
(ii) Where will the image be formed if he shifts the candle towards the lens at a position of .
(iii) What will be the nature of the image formed if he further shifts the candle towards the lens ?
(iv) Draw a ray diagram to show the formation of the image in case (iii) as said above.
Step-by-Step Solution
1. Identify Object Distance (u):
- The object distance (u) is the distance from the lens to the candle.
- u=Position of lens−Position of candle=50.0cm−12.0cm=38.0cm
- According to sign conventions, u=−38.0cm.
2. Identify Image Distance (v):
- The image distance (v) is the distance from the lens to the screen.
- v=Position of screen−Position of lens=88.0cm−50.0cm=38.0cm
- According to sign conventions, v=+38.0cm.
3. Use the Lens Formula:
- The lens formula is given by:
1f=1v−1u
- Substituting the values:
1f=138−1−38=138+138=238=119
- Therefore, the focal length f=19.0cm.
(ii) Finding the Image Position when the Candle is at 31.0 cm:
1. New Object Distance (u):
- The new position of the candle is 31.0 cm.
- u=Position of lens−Position of candle=50.0cm−31.0cm=19.0cm
- According to sign conventions, u=−19.0cm.
2. Using the Lens Formula:
- We already know f=19.0cm.
- Substitute into the lens formula:
1f=1v−1u
119=1v−1−19
119=1v+119
- Rearranging gives:
1v=119−119=0
- Thus, v approaches infinity. The image is formed at infinity.
(iii) Nature of the Image when Candle is Further Shifted Towards the Lens:
- If the candle is moved closer to the lens, it will be placed between the focal point and the lens.
- In this case, the image formed will be:
- Virtual
- Erect
- Enlarged
(iv) Ray Diagram for the Case in (iii):
1. Draw the Lens:
- Draw a convex lens in the center.
2. Mark the Focal Points:
- Mark the focal points on both sides of the lens.
3. Position the Candle:
- Place the candle between the lens and the focal point on the same side as the candle.
4. Draw the Rays:
- Draw one ray parallel to the principal axis that passes through the lens and refracts through the focal point on the opposite side.
- Draw another ray passing through the center of the lens that continues in a straight line.
- Extend the refracted rays backward to find the position of the virtual image.
5. Label the Image:
- Indicate that the image is virtual, erect, and enlarged.
- The object distance (u) is the distance from the lens to the candle.
- u=Position of lens−Position of candle=50.0cm−12.0cm=38.0cm
- According to sign conventions, u=−38.0cm.
- The image distance (v) is the distance from the lens to the screen.
- v=Position of screen−Position of lens=88.0cm−50.0cm=38.0cm
- According to sign conventions, v=+38.0cm.
- The lens formula is given by:
1f=1v−1u
- Substituting the values:
1f=138−1−38=138+138=238=119
- Therefore, the focal length f=19.0cm.
- The new position of the candle is 31.0 cm.
- u=Position of lens−Position of candle=50.0cm−31.0cm=19.0cm
- According to sign conventions, u=−19.0cm.
- We already know f=19.0cm.
- Substitute into the lens formula:
1f=1v−1u
119=1v−1−19
119=1v+119
- Rearranging gives:
1v=119−119=0
- Thus, v approaches infinity. The image is formed at infinity.
- In this case, the image formed will be:
- Virtual
- Erect
- Enlarged
- Draw a convex lens in the center.
- Mark the focal points on both sides of the lens.
- Place the candle between the lens and the focal point on the same side as the candle.
- Draw one ray parallel to the principal axis that passes through the lens and refracts through the focal point on the opposite side.
- Draw another ray passing through the center of the lens that continues in a straight line.
- Extend the refracted rays backward to find the position of the virtual image.
- Indicate that the image is virtual, erect, and enlarged.
Topper's Solved these Questions
- LIGHT : REFLECTION AND REFRACTIONBook:NCERT EXEMPLAR ENGLISHChapter:LIGHT : REFLECTION AND REFRACTIONExercise:Short Answer Type Questions
Explore 10 Videos
- ELECTRICITYBook:NCERT EXEMPLAR ENGLISHChapter:ELECTRICITYExercise:Short Answer Type Questions
Explore 17 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENT Book:NCERT EXEMPLAR ENGLISHChapter:MAGNETIC EFFECTS OF ELECTRIC CURRENT Exercise:LONG ANSWER TYPE QUESTIONS
Explore 8 Videos
Similar Questions
A student focussed the flame of a candle on a screen with the help of a convex lens. He noted the positions of candle, lens and screen on the scale as given below:
Position of candle = 14.0 cm, Position of convex lens = 50.0 cm, Position of screen = 86.0 cm
(i) Find the focal length of the lens.
(ii) If under the given condition, height of the flame is 1.5 cm, what would be the height of image obtained on the screen?
(iii) If he displaces the candle to 32.0 cm, where will the image be formed and what will be its nature? Give reason for your answer.
(iv) After this if he further displaces the candle towards the lens, what will be the nature of the image formed and where will it be?
(v) Draw a ray diagram to show the formation of image in the above mentioned case.
[Hints. (i) u = (50-14) cm = 36 cm, v = (86 - 50) cm = 36 cm.
Thus the object is at 2f. Therefore f = 18cm
(ii) Height will be same, i.e., 1.5 cm
(iii) u = 50-32 = 18 cm. Thus, object will be at focus. Therefore, image will be at infinity and is real, inverted and enlarged.
(iv) Object will come in between focus and optical centre.
Image will be virtual, erect and enlarged and formed on the same side of lens as the object.
View SolutionFocal length of the convex lens shown in figure is 20cm. Find the image position and image velocity.
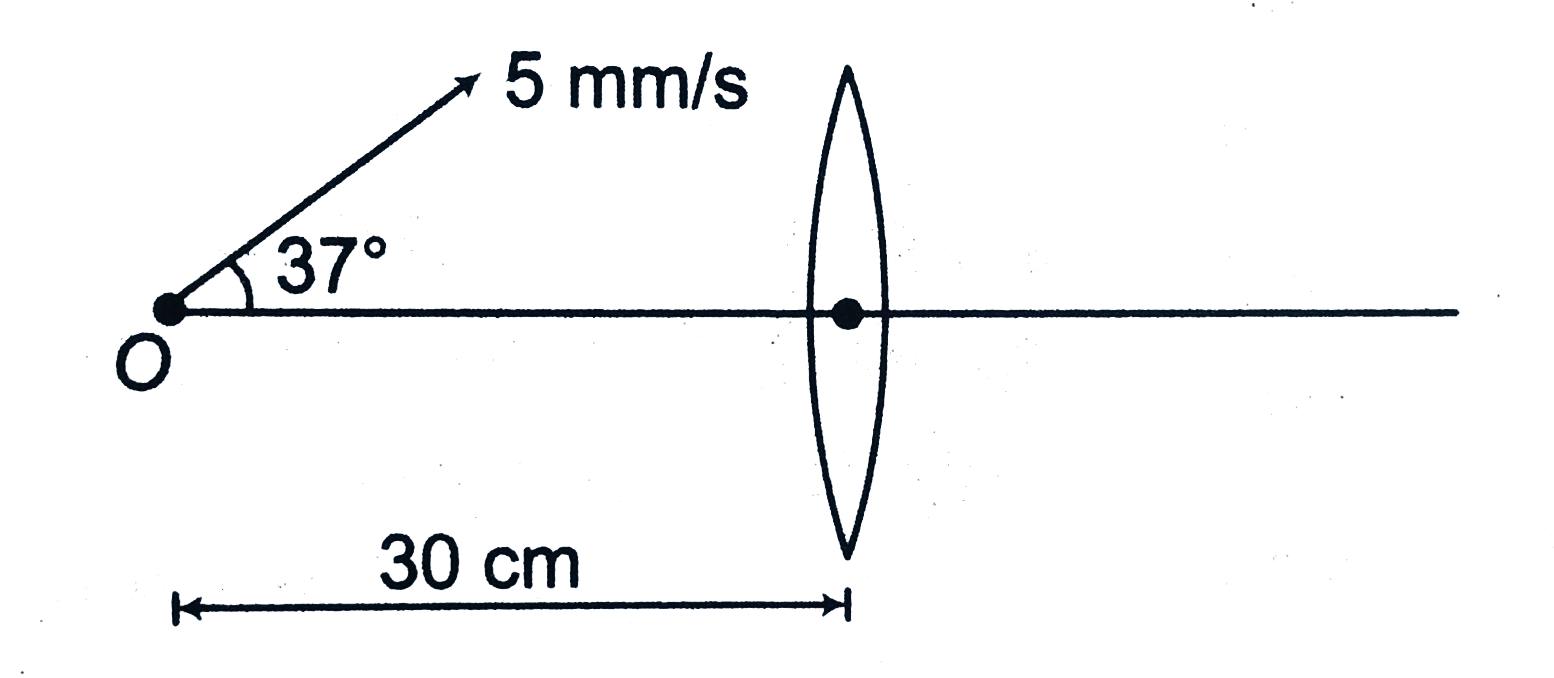
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
(i) What is the nature of the image so formed ?
(ii) Calculate the distance of the image from the lens.
(iii) Calculate the magnification of the image.
View SolutionFocal length of a convex lense in air is 20cm. and of concave lens 40cm. Find the position of final image.
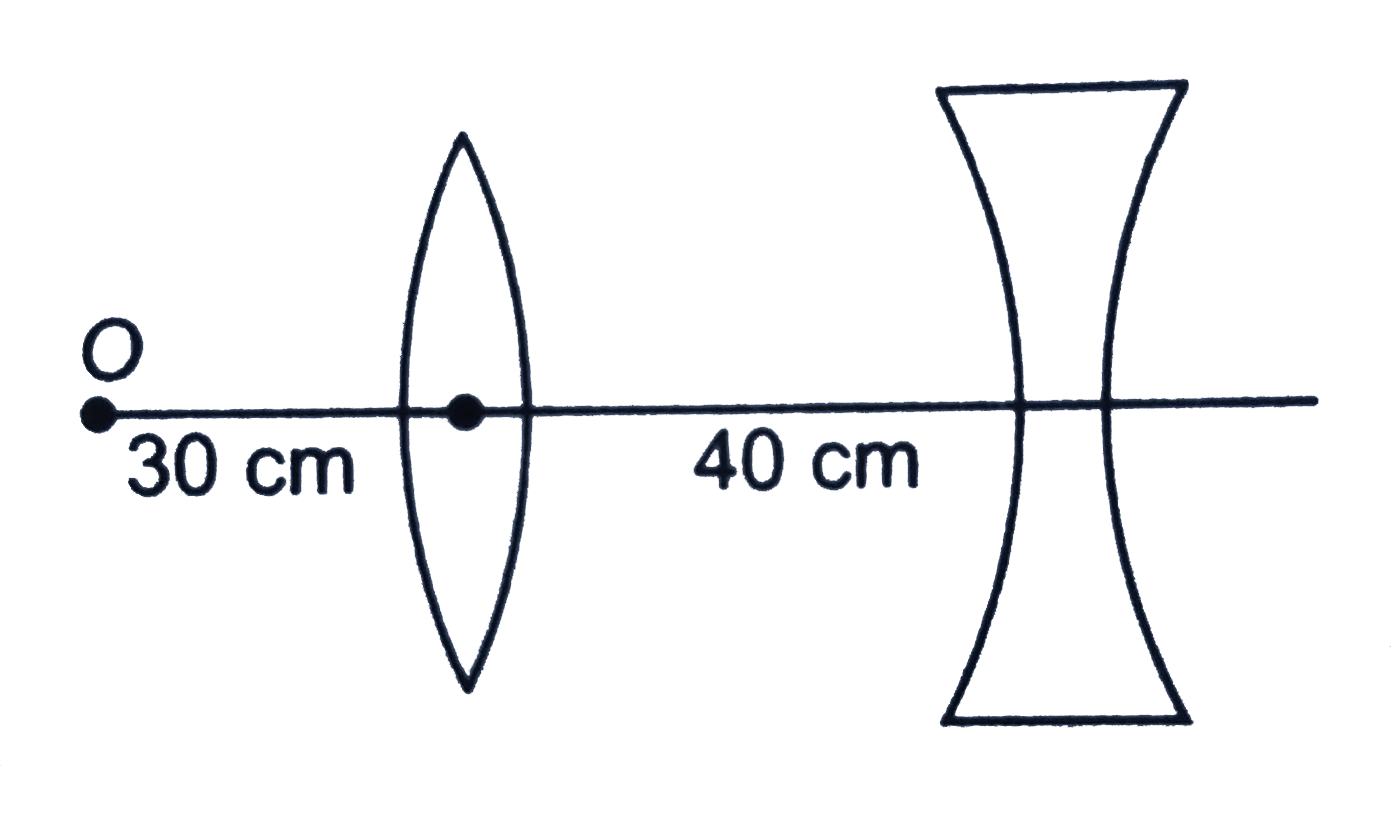
View SolutionGraph of position of image vs position of point object from a convex lens is shown. Then, focal length of the lens is
_E01_287_Q01.png)
View SolutionA biconvex lens is used to project a slide on screen. The slide is 2cm high and placed at 10cm from the lens. The image is 18cm high. What is the focal length of the lens?
View SolutionIn displacement method, there are two position of a lens for which we get clear image. First position of the lens is at 40 cm from object and second is at 80 cm, the focal length of lens is
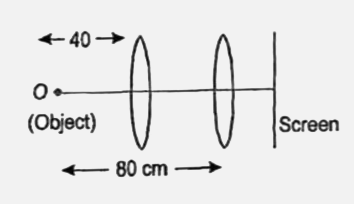
View SolutionA lens placed between a candle and a fixed screen forms a real triply magnified image of the candle on the screen. When the lens is moved away form the candle by 0.8m without changing the position of the candle, a real image one-third the size of the candle is formed on the screen. Determine the focal length of the lens.
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionThe figure below shows the positions of a point object 0, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
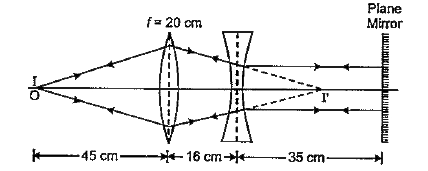
View Solution