A student in a lab took a coil and connected it to a 12VDC source. He measures the steady state current in the circuit to be 4A. He then replaced the 12VDC source by a 12V,(ω=50rads)AC source and observes that the reading in the AC ammeter is 2.4A. He then decides to connect a 2500μF capacitor in series with the coil and calculate the average power developed in the circuit. Further he also decides to study the variation in current in the circuit (with the capacitor and the battery in series).
Which of the following graph roughly matches the variation of current in the circuit (with the coil and capacitor connected in the series) when the angulr frequency is decreased from 50 rad/s to 25 rad/s?
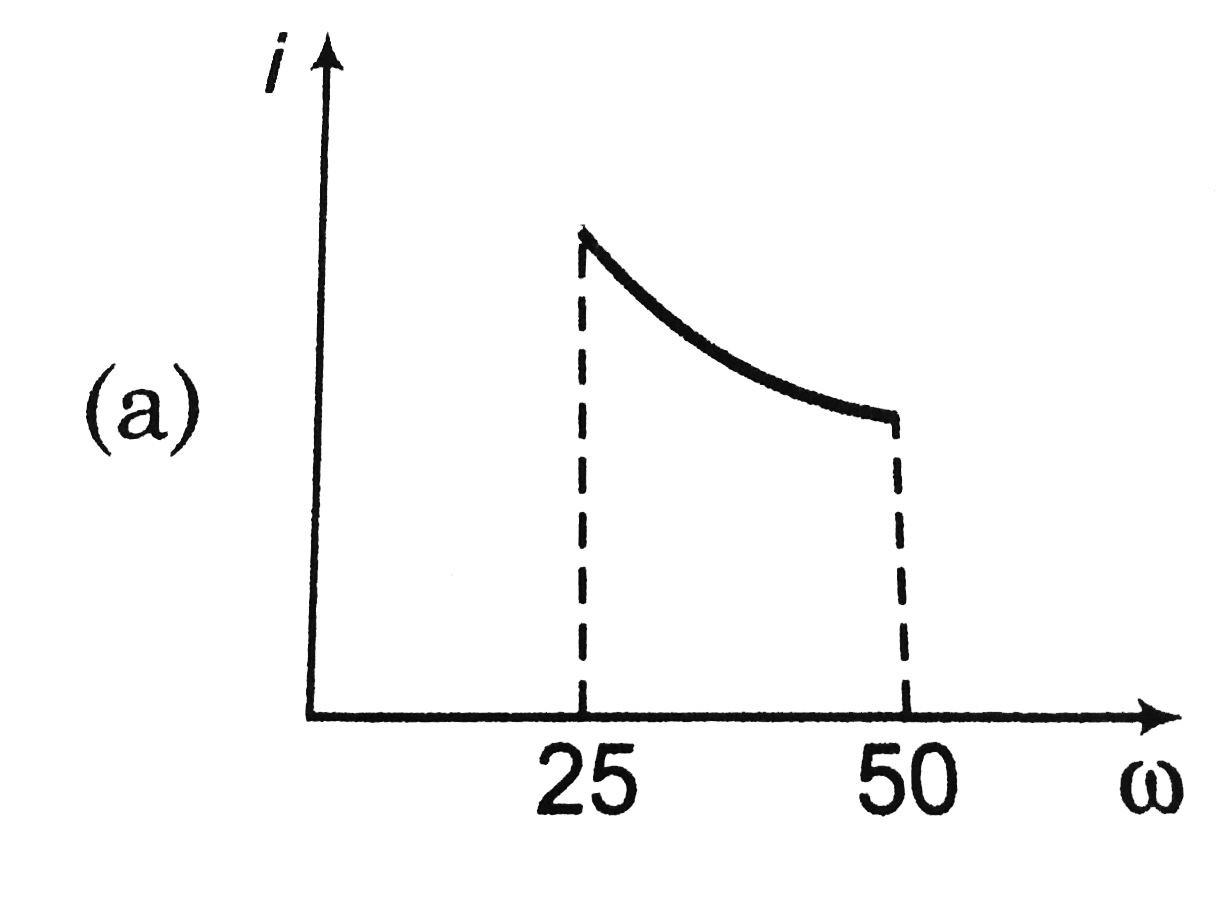
The correct Answer is:B
To solve the problem, we need to analyze the behavior of the circuit when a capacitor is added in series with an inductor (coil) and how the current varies with a change in angular frequency. Here’s a step-by-step breakdown:
Step 1: Understand the Circuit Components
- The circuit consists of a coil (inductor) and a capacitor connected in series.
- The initial measurements were taken with a DC source and then with an AC source at an angular frequency of ω=50rad/s.
Step 2: Calculate the Impedance of the Circuit
1. Impedance Formula: For a series RLC circuit, the impedance Z is given by:
Z=√R2+(XL−XC)2
where R is the resistance, XL is the inductive reactance, and XC is the capacitive reactance.
2. Given Values:
- From the DC circuit, the resistance R can be calculated using Ohm's law:
R=VI=12V4A=3Ω
- The AC current is given as 2.4A at ω=50rad/s.
3. Calculate XL:
- The inductive reactance XL can be calculated using:
I=VZ⟹Z=VI=12V2.4A=5Ω
- Rearranging the impedance formula gives:
5=√32+(XL−XC)2
- Solving for (XL−XC):
52=9+(XL−XC)2⟹25−9=(XL−XC)2⟹(XL−XC)2=16⟹|XL−XC|=4
Step 3: Calculate Capacitive Reactance
1. Capacitive Reactance:
- The capacitive reactance XC is given by:
XC=1ωC
- Given C=2500μF=2500×10−6F:
- At ω=50rad/s:
XC=150×2500×10−6=10.125=8Ω
Step 4: Analyze the Effect of Decreasing Angular Frequency
1. Decrease ω:
- When ω decreases from 50rad/s to 25rad/s, XC increases:
XC=125×2500×10−6=10.05=20Ω
2. Calculate New Impedance:
- The new impedance Z when ω=25rad/s:
Z=√R2+(XL−XC)2
- Since XL−XC will now be 4−20=−16:
Z=√32+(−16)2=√9+256=√265≈16.28Ω
Step 5: Calculate the New Current
- The new current I can be calculated using:
I=VZ=12V16.28Ω≈0.737A
Step 6: Graphical Representation
- As the angular frequency decreases, the current decreases due to the increase in capacitive reactance, resulting in a higher impedance.
- The graph that represents the current variation as ω decreases from 50rad/s to 25rad/s would show a decreasing trend in current.
Conclusion
The correct graph that matches the variation of current in the circuit when the angular frequency is decreased from 50rad/s to 25rad/s is the one showing a decrease in current.
- The circuit consists of a coil (inductor) and a capacitor connected in series.
- The initial measurements were taken with a DC source and then with an AC source at an angular frequency of ω=50rad/s.
1. Impedance Formula: For a series RLC circuit, the impedance Z is given by:
Z=√R2+(XL−XC)2
where R is the resistance, XL is the inductive reactance, and XC is the capacitive reactance.
- From the DC circuit, the resistance R can be calculated using Ohm's law:
R=VI=12V4A=3Ω
- The AC current is given as 2.4A at ω=50rad/s.
- The inductive reactance XL can be calculated using:
I=VZ⟹Z=VI=12V2.4A=5Ω
- Rearranging the impedance formula gives:
5=√32+(XL−XC)2
- Solving for (XL−XC):
52=9+(XL−XC)2⟹25−9=(XL−XC)2⟹(XL−XC)2=16⟹|XL−XC|=4
1. Capacitive Reactance:
- The capacitive reactance XC is given by:
XC=1ωC
- Given C=2500μF=2500×10−6F:
- At ω=50rad/s:
XC=150×2500×10−6=10.125=8Ω
1. Decrease ω:
- When ω decreases from 50rad/s to 25rad/s, XC increases:
XC=125×2500×10−6=10.05=20Ω
- The new impedance Z when ω=25rad/s:
Z=√R2+(XL−XC)2
- Since XL−XC will now be 4−20=−16:
Z=√32+(−16)2=√9+256=√265≈16.28Ω
- The new current I can be calculated using:
I=VZ=12V16.28Ω≈0.737A
- As the angular frequency decreases, the current decreases due to the increase in capacitive reactance, resulting in a higher impedance.
- The graph that represents the current variation as ω decreases from 50rad/s to 25rad/s would show a decreasing trend in current.
The correct graph that matches the variation of current in the circuit when the angular frequency is decreased from 50rad/s to 25rad/s is the one showing a decrease in current.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Subjective
10 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
62 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2More Than One Correct
8 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
A student in a lab took a coil and connected it to a 12VDC source. He measures the steady state current in the circuit to be 4A. He then replaced the 12VDC source by a 12V,(ω=50rad/s)AC source and observes that the reading in the AC ammeter is 2.4A. He then decides to connect a 2500μF capacitor in series with the coil and calculate the average power developed in the circuit. Further he also decides to study the variation in current in the circuit (with the capacitor and the battery in series).
The value of resistance of the coil calculated by the student is
View SolutionA student in a lab took a coil and connected it to a 12VDC source. He measures the steady state current in the circuit to be 4A. He then replaced the 12VDC source by a 12V,(ω=50rad/s)AC source and observes that the reading in the AC ammeter is 2.4A. He then decides to connect a 2500μF capacitor in series with the coil and calculate the average power developed in the circuit. Further he also decides to study the variation in current in the circuit (with the capacitor and the battery in series).
The power developed in te circuit when the capcitor of 2500 μF is connected in sereis with the coil is
View SolutionA 0.21 H inductor and a 12Ω resistance are connected in series to a 220 V, 50 Hz ac source.
The current in the circuit is
View SolutionA resistance is connected to a n AC source. If a capacitor is induced in the series cirucit, the average power absorbed by the resistance
View SolutionA 100W bulb is connected to an AC source of 220V, 50Hz. Then the current flowing through the bulb is
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA long solenoid connected to a 12V DC source passes a steady current of 2 A. When the solenoid is connected to an AC source of 12V at 50 Hz, the current flowing is 1A. Calculate inductance of the solenoid.
View SolutionA 0.21H inductor and a 12ohm resistance are connected in series to a 220V. 50Hz ac source. Calculate the current in the circuit and the phase angle between the current and the source voltage.
View Solution
