A student sits on a stool that is free to rotate about a vertical axis. He holds out his arms horizontally, with a 4-kg weight in each hand. The stool is set in rotation with angular speed of 0.5 revolution per second. Calcualate the angular speed of the student is 90 cm and his rotational inertia is 7kg m2.
[Hint: Use conservation principle]
The correct Answer is:0.96 rev/sec.
Step by step video, text & image solution for A student sits on a stool that is free to rotate about a vertical axis. He holds out his arms horizontally, with a 4-kg weight in each hand. The stool is set in rotation with angular speed of 0.5 revolution per second. Calcualate the angular speed of the student is 90 cm and his rotational inertia is 7kg m^(2). [Hint: Use conservation principle] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises42videos
ROTATIONAL DYNAMICS, MOMENT OF INERTIA
- BOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises33videos
MOMENT, TORQUE, EQUILIBRIUM OF BODIES
- BOOK - NN GHOSHCHAPTER - SATURATED AND UNSATURATED VAPOUREXERCISE - All Questions1videos
SATURATED AND UNSATURATED VAPOUR
Similar Questions
A uniform rod of length 1m and mass 0.5kg rotates at angular speed of 6rad/sec about one of its ends. What is the KE (in joule) of the rod ?
View SolutionFigure shows a student, sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose moment of inertia is I about its central axis. The wheel is rotating at an angular speed ωi from an overead perspective, the rotation is counter clockwise. The axis of the wheel point vertical, and the angular momentum →Li of the wheel points vertically upward. The student now inverts the wheel, as a result, the student and stool rotate about the stool axis. With what angular speed and direction does the student then rotate? (The moment of inertia of the student+stool+wheel system about the stool axis is I0)

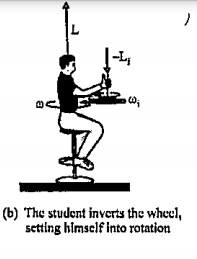 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A fan of moment of inertia 0.6 kg × metre2 is to run upto a working speed of 0.5 revolution per second. Indicate the correct value of the angular momentum of the fan
A0.6πkg×metre2secB6πkg×metre2secC3πkg×metre2secDπ6kg×metre2sec - Question 2 - Select One
A man stands at the centre of a circular table with his two hands outstretched. The table is set into rotation with an angular speed of 40 rev/min. What is the angular speed when the man folds his hands back and thereby reduces his moment of inertia 2/5 times the initial value? Assume that the table rotates without friction.
AA) 100 rpmBB) 150 rpmCC) 50 rpmDD) 75 rpm - Question 3 - Select One
A dancer is standing on a stool rotating about the vertical axis passing through its centre. She pulls her arms towards the body reducing her moment of inertia by factor of n. The new angular speed of turn table is proportional to :
AnBn−1Cn∘Dn2
(i) A child stands at the centre of turntable with his two arms out stretched. The turntable is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 23 times the initial value ? Assume that the turntable rotates without friction
(ii) Show that the child's new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy ?View SolutionA dancer is standing on a stool rotating about the vertical axis passing through its centre. She pulls her arms towards the body reducing her moment of inertia by a factor of n. The new angular speed of turn table is proportional to
View SolutionA wheel of mass 2 kg and radius 20 cm initially at rest is free to rotate about its axis. It receives an angular impulse of 4kgm2s−1 initially and similar impulse after every 5 s of initial one. Calculate the angular speed of the wheel 22 s after the initial impulse.
View SolutionA dancer is standing on a stool rotating about the vertical axis passing through its centre. She pulls her arms towards the body reducing her moment of inertia by factor of n. The new angular speed of turn table is proportional to :
View SolutionA student sits on a freely rotating stool holding dumbbells, each of mass 5.0kg (Fig). When his arms are extended horizontally (Fig a), the dumbbells are 1.0m from the axis of rotation and the student rotate with an angular speed of 1.0rad/s. The moment of inertia of the student plus stool is 5.0kg.m2 and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position 0.50m from the rotationa are (Fig.) The new angular speed of the student is.
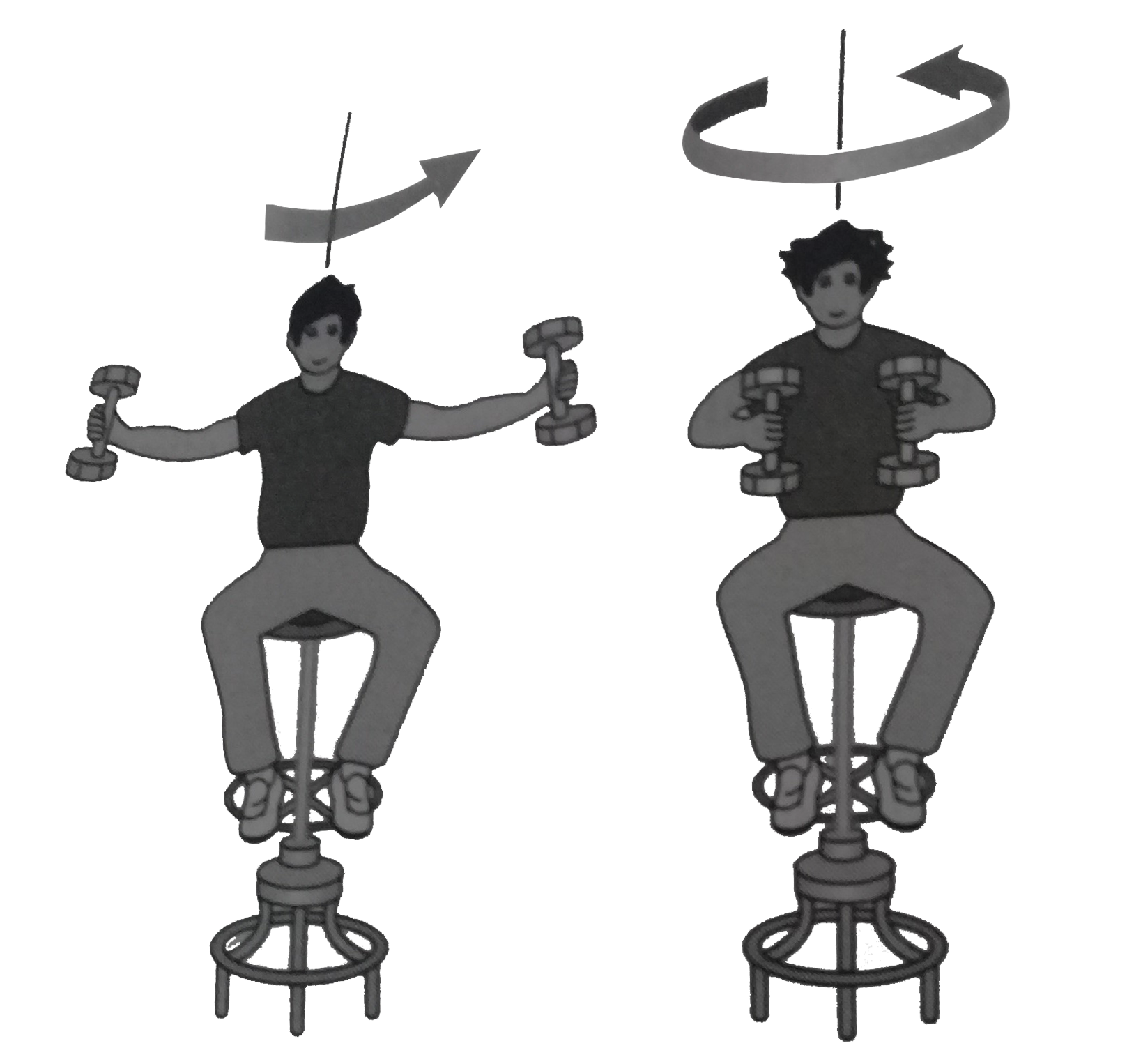 .View Solution
.View Solution

