A student wants to determine the coefficients of static frction and kinetic friciton between a box and a plank. She places the box on the plank and gradually raises on end on of the plank. When the angle of inclination with horizontal reaches 30∘ , the box stars to slip, and it then slides 2.5m dwon the plank in 4.0 s at constant acceleration. What are (a) the coefficient of static frictio and (b) the coefficient of kinetic friction between the box and the plank ?
To solve the problem of determining the coefficients of static and kinetic friction between a box and a plank, we can follow these steps:
Step 1: Analyze the Forces Acting on the Box
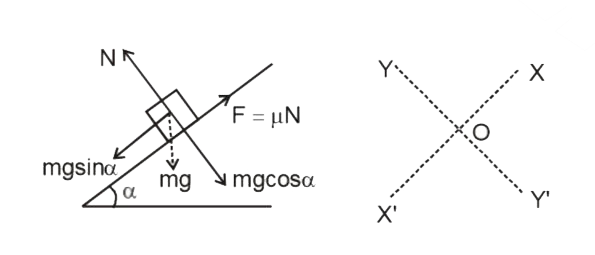
When the box is on the inclined plank at an angle of 30∘, the forces acting on it are:
- The weight of the box W=mg acting downwards.
- The normal force N acting perpendicular to the surface of the plank.
- The frictional force Ff acting parallel to the surface of the plank, opposing the motion.
The weight can be resolved into two components:
- Perpendicular to the plank: W⊥=mgcos(30∘)
- Parallel to the plank: W∥=mgsin(30∘)
Step 2: Determine the Coefficient of Static Friction (μs)
At the point just before slipping occurs, the maximum static friction force Ffmax equals the component of the weight acting down the incline:
Ffmax=μsN
Where N=mgcos(30∘).
Setting the forces equal gives:
μsmgcos(30∘)=mgsin(30∘)
Cancelling mg from both sides:
μscos(30∘)=sin(30∘)
Using the values sin(30∘)=12 and cos(30∘)=√32:
μs⋅√32=12
Solving for μs:
μs=1/2√3/2=1√3≈0.577
Step 3: Calculate the Acceleration of the Box
The box slides down the plank with a constant acceleration. Given that it slides 2.5 m in 4.0 s, we can use the equation of motion:
s=ut+12at2
Where s=2.5m, u=0 (initial velocity), and t=4.0s.
Substituting the values:
2.5=0⋅4+12a(42)
2.5=12a(16)
a=2.5⋅216=516m/s2
Step 4: Determine the Coefficient of Kinetic Friction (μk)
When the box is sliding, the net force acting on it is:
Fnet=mgsin(30∘)−Fk
Where Fk=μkN.
Thus:
Fnet=mgsin(30∘)−μkmgcos(30∘)
Using Newton's second law:
Fnet=ma
Setting the two expressions equal gives:
mgsin(30∘)−μkmgcos(30∘)=ma
Cancelling mg from both sides:
sin(30∘)−μkcos(30∘)=ag
Substituting sin(30∘)=12, cos(30∘)=√32, and a=516:
12−μk⋅√32=516g
Assuming g≈9.8m/s2:
516⋅9.8≈0.032
Rearranging gives:
μk⋅√32=12−0.032
μk⋅√32=0.468
μk=0.468⋅2√3≈0.54
Final Answers
(a) The coefficient of static friction μs≈0.577
(b) The coefficient of kinetic friction μk≈0.54
When the box is on the inclined plank at an angle of 30∘, the forces acting on it are:
- The weight of the box W=mg acting downwards.
- The normal force N acting perpendicular to the surface of the plank.
- The frictional force Ff acting parallel to the surface of the plank, opposing the motion.
- Perpendicular to the plank: W⊥=mgcos(30∘)
- Parallel to the plank: W∥=mgsin(30∘)
At the point just before slipping occurs, the maximum static friction force Ffmax equals the component of the weight acting down the incline:
Ffmax=μsN
Where N=mgcos(30∘).
μsmgcos(30∘)=mgsin(30∘)
μscos(30∘)=sin(30∘)
μs⋅√32=12
μs=1/2√3/2=1√3≈0.577
The box slides down the plank with a constant acceleration. Given that it slides 2.5 m in 4.0 s, we can use the equation of motion:
s=ut+12at2
Where s=2.5m, u=0 (initial velocity), and t=4.0s.
2.5=0⋅4+12a(42)
2.5=12a(16)
a=2.5⋅216=516m/s2
When the box is sliding, the net force acting on it is:
Fnet=mgsin(30∘)−Fk
Where Fk=μkN.
Fnet=mgsin(30∘)−μkmgcos(30∘)
Fnet=ma
Setting the two expressions equal gives:
mgsin(30∘)−μkmgcos(30∘)=ma
sin(30∘)−μkcos(30∘)=ag
12−μk⋅√32=516g
516⋅9.8≈0.032
μk⋅√32=12−0.032
μk⋅√32=0.468
μk=0.468⋅2√3≈0.54
(a) The coefficient of static friction μs≈0.577
(b) The coefficient of kinetic friction μk≈0.54
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)23videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
A box is lying on an inclined plane if the box slides when the angle of inclination is 60∘ then the coefficient of static friction of the box and the plane is?
View SolutionA wooden block is kept n a polished woden plank and the inclination of the plank is gradually increased. It is found that the block starts slipping when the pland makes an angle of 18∘ with the horizontal. However, once started the block can continue with uniform speed if the inclination is reduced to 15∘. Find the coefficients of static and kinetic friction between the block and the plank.
View Solution
Knowledge Check
- Question 1 - Select One
A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches 30∘ , the box starts to slip and slide 4.0m down the plank in 4.0s . The coefficients of static and kinetic friction between the box and the plank will be, respectively.
 A0.4 and 0.3B0.6 and 0.6C0.6 and 0.5D0.5 and 0.6
A0.4 and 0.3B0.6 and 0.6C0.6 and 0.5D0.5 and 0.6 - Question 2 - Select One
A box is lying on an inclined plane what is the coefficient of static friction if the box starts sliding when an angle of inclination is 60∘
A1.173B1.732C2.732D1.677
A wooden block is kept on a polished wooden plank whose inclination is increased gradully . The block starts slipping when the plank makes an angle of 25∘ with the horizontal . However , once started , the block can continue with unifrom speed , if the inclination is reduced to 21 Calculate coefficient of static and dynamic friction between the block and the plank .
View SolutionA 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
 View Solution
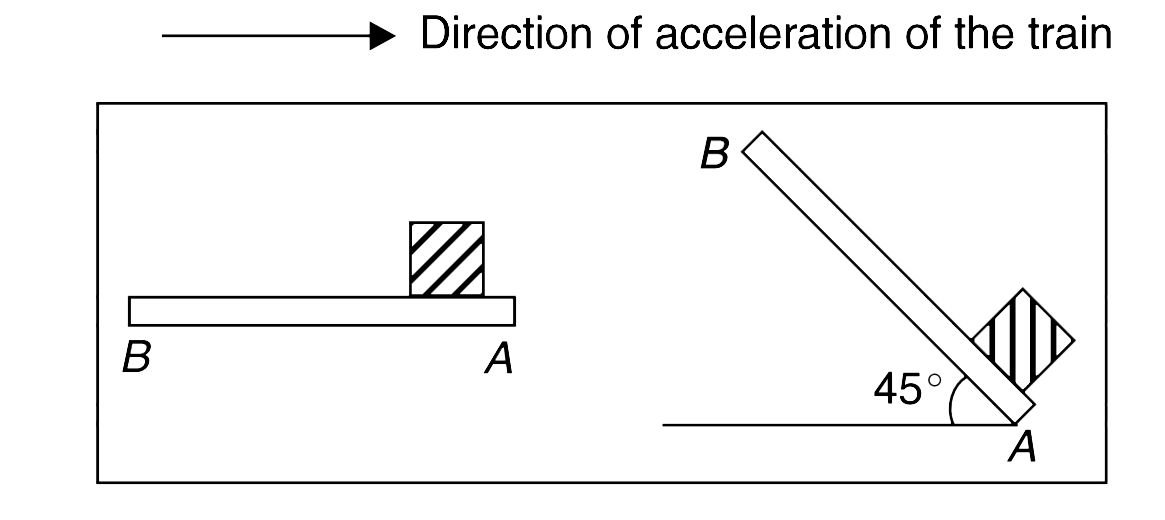
View SolutionAn experimenter is inside a uniformly accelerated train. Train is moving horizontally with constant acceleration a0. He places a wooden plank AB in horizontal position with end A pointing towards the engine of the train. A block is released at end A of the plank and it reaches end B in time t1. The same plank is placed at an inclination of 45∘ to the horizontal. When the block is released at A it now climbs to B in timet2. It was found that t2t1=254. What is the coefficient of friction between the block and the plank?
 View Solution
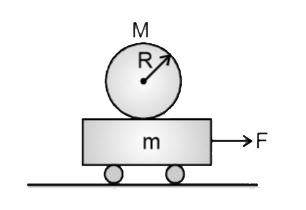
View SolutionDetermine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μsandμk respectively.
 View Solution
View SolutionA thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v0 and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is μ.
 View Solution
View SolutionA long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t2 for 0≤t≤2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m/s2)
View Solution

