A supercondutig round ring of radius a and inductance L was located in a unifrom magnetic fied of induction B. The ring plane was parallel to the vector B, and the current in the ring was equal to zero. Them the ring was turned through 90∘ so that its plane became perpendicular to the feild. FInd:
(a) the current induced in the ring after the turn,
(b) the work perfromed during the turn.
In a superconductor there is no resistance, Hence,
LdIdt+dΦdt
So intergating I=ΔΦL=πa2BL
because ΔΦ=Φf−Φi,Φf=πa2B,Φi=0
Also, the work done is A=∫ξIdt=∫dΦdt=12LI2=12π2a4B2L
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
A supereconducting round ring of radius a and inductance L was located in a uniform in a uniform magnetic field of induction B . The ring plane was parallel to the vector B and the current in the ring was equal to zero, then the ring was turned through 90∘ so that its plane became perpendicular to the field. Find
(a) the current induced in the ring after the turn
(b) the work performed during the turn.View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View Solution
Knowledge Check
- Question 1 - Select One or More
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
AIt is rotated about it axisBit is translatedCit is rotated about a diameterDit is deformed - Question 2 - Select One
A metal ring of radius r=0.5m with its plane noraml a unifrom magnetic field B of induction 0.2T carries a current I=100A The tension in newtons develoed in the ring is
A100B50C25D10 - Question 3 - Select One or More
A vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,
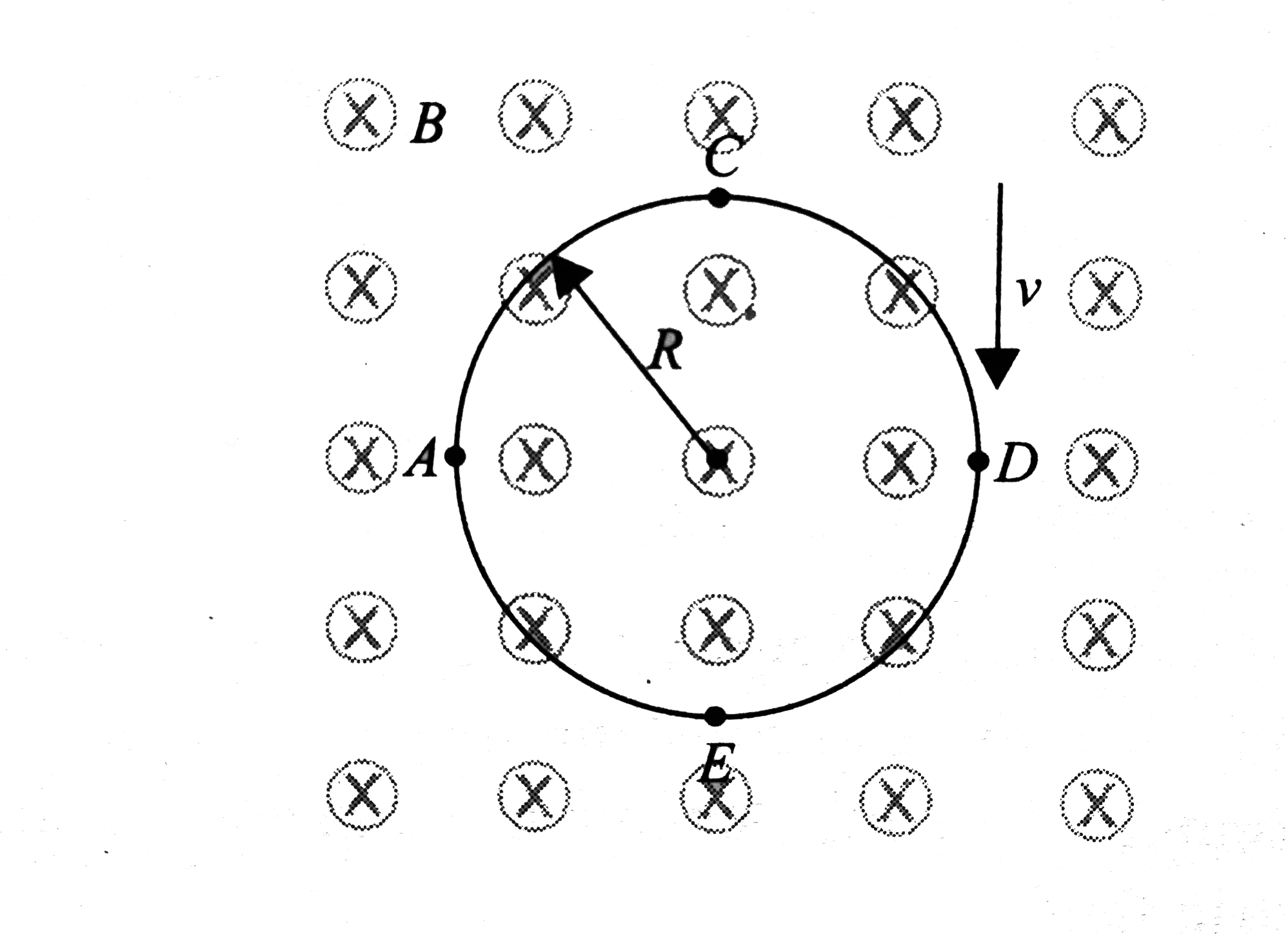 A(a) no current flows in the ringB(b) AandD are at the same potentialC( c) CandE are at the same potentialD(d) the potential difference between AandD is 2BRv, with D at a higher potetial
A(a) no current flows in the ringB(b) AandD are at the same potentialC( c) CandE are at the same potentialD(d) the potential difference between AandD is 2BRv, with D at a higher potetial
A ring radius a=50mm made of thin wire of radius b=1.0mm was located in a unifrom magnetic field with induction B=0.50mT so that the ring place was perpenficular to the vector B. Then the ring was cooled down to superconducting state, and the magnetic field was swichted off. Find the ring current after that. Note that the inductiance of a thin ring along which the surface current flows is equal to L=μ0a(In8ab−2).
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
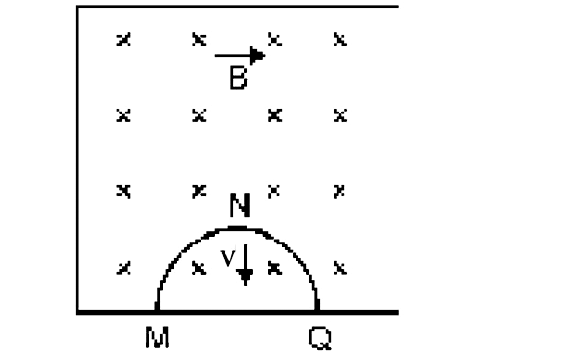
View SolutionA thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
 View Solution
View SolutionA thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is
 View Solution
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
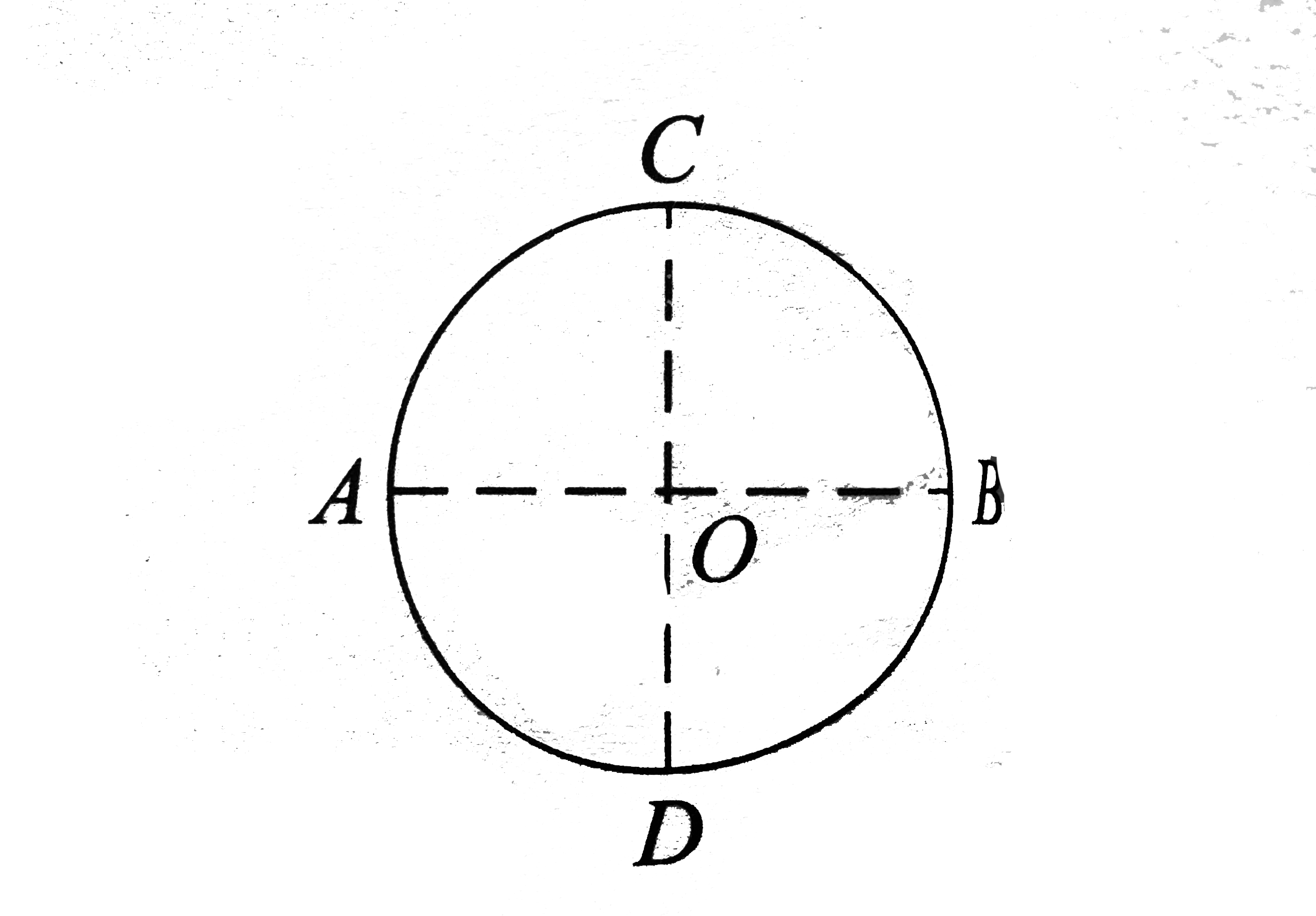 View Solution
View Solution

