A swimmer capable of swimming with velocity v relative to water jumps in a flowing river having velocity u. The man swims a distance d down stream and returns back to the original position. Find out the time taken in complete motion.
To solve the problem of the swimmer swimming in a river, we can break it down into a few steps. The swimmer swims downstream and then returns upstream to the original position. We need to find the total time taken for this complete motion.
1. Identify the velocities:
- The swimmer's velocity relative to water is v.
- The river's velocity is u.
2. Calculate the effective velocities:
- When swimming downstream (with the current), the effective velocity of the swimmer is:
vdown=v+u
- When swimming upstream (against the current), the effective velocity of the swimmer is:
vup=v−u
3. Calculate the time taken for each segment:
- The distance traveled downstream is d. The time taken to swim downstream is:
tdown=dv+u
- The distance traveled upstream is also d. The time taken to swim upstream is:
tup=dv−u
4. Calculate the total time taken:
- The total time taken for the complete motion (downstream and upstream) is:
ttotal=tdown+tup=dv+u+dv−u
5. Combine the fractions:
- To combine the two fractions, we find a common denominator:
ttotal=d(v−u)+d(v+u)(v+u)(v−u)
- Simplifying the numerator:
ttotal=d(v−u+v+u)(v+u)(v−u)=d(2v)(v+u)(v−u)
6. Final expression for total time:
- Thus, the total time taken for the swimmer to swim downstream and return upstream is:
ttotal=2dvv2−u2
Final Answer:
The total time taken for the complete motion is:
ttotal=2dvv2−u2
- The swimmer's velocity relative to water is v.
- The river's velocity is u.
- When swimming downstream (with the current), the effective velocity of the swimmer is:
vdown=v+u
- When swimming upstream (against the current), the effective velocity of the swimmer is:
vup=v−u
- The distance traveled downstream is d. The time taken to swim downstream is:
tdown=dv+u
- The distance traveled upstream is also d. The time taken to swim upstream is:
tup=dv−u
- The total time taken for the complete motion (downstream and upstream) is:
ttotal=tdown+tup=dv+u+dv−u
- To combine the two fractions, we find a common denominator:
ttotal=d(v−u)+d(v+u)(v+u)(v−u)
- Simplifying the numerator:
ttotal=d(v−u+v+u)(v+u)(v−u)=d(2v)(v+u)(v−u)
- Thus, the total time taken for the swimmer to swim downstream and return upstream is:
ttotal=2dvv2−u2
The total time taken for the complete motion is:
ttotal=2dvv2−u2
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionA boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionA boatman moves his boat with a velocity 'v' (relative to water) in river and finds to his surprise that velocity of river 'u' (with respect to ground) is more than 'v'. He has to reach a point directly opposite to the starting point on another bank by travelling minimum possible distance. Then
View SolutionA person can swim in still water at 5 m/s. He moves in a river of velocity 3 m/s. First down the stream next same distance up the steam the ratio of times taken are
View SolutionA swimmer is capable of swimming at 1.65ms- in still water. If he swims directly across a 180m wide river with water flow at 0.85ms−1', how far down stream will he reach? How long will it take to reach the other side ?
View SolutionThe velocity if a swimmer (v) in stil water is less than the velocity of water (u) in a river. Show that the swimmer must aim himself at an angles cos−1 (v/u) with upstream in order to cross the river along the shortest possible path. Find thr drifting (distance moved along the direction of stream in crossing the river) of the swimmer along this shortest possible path.
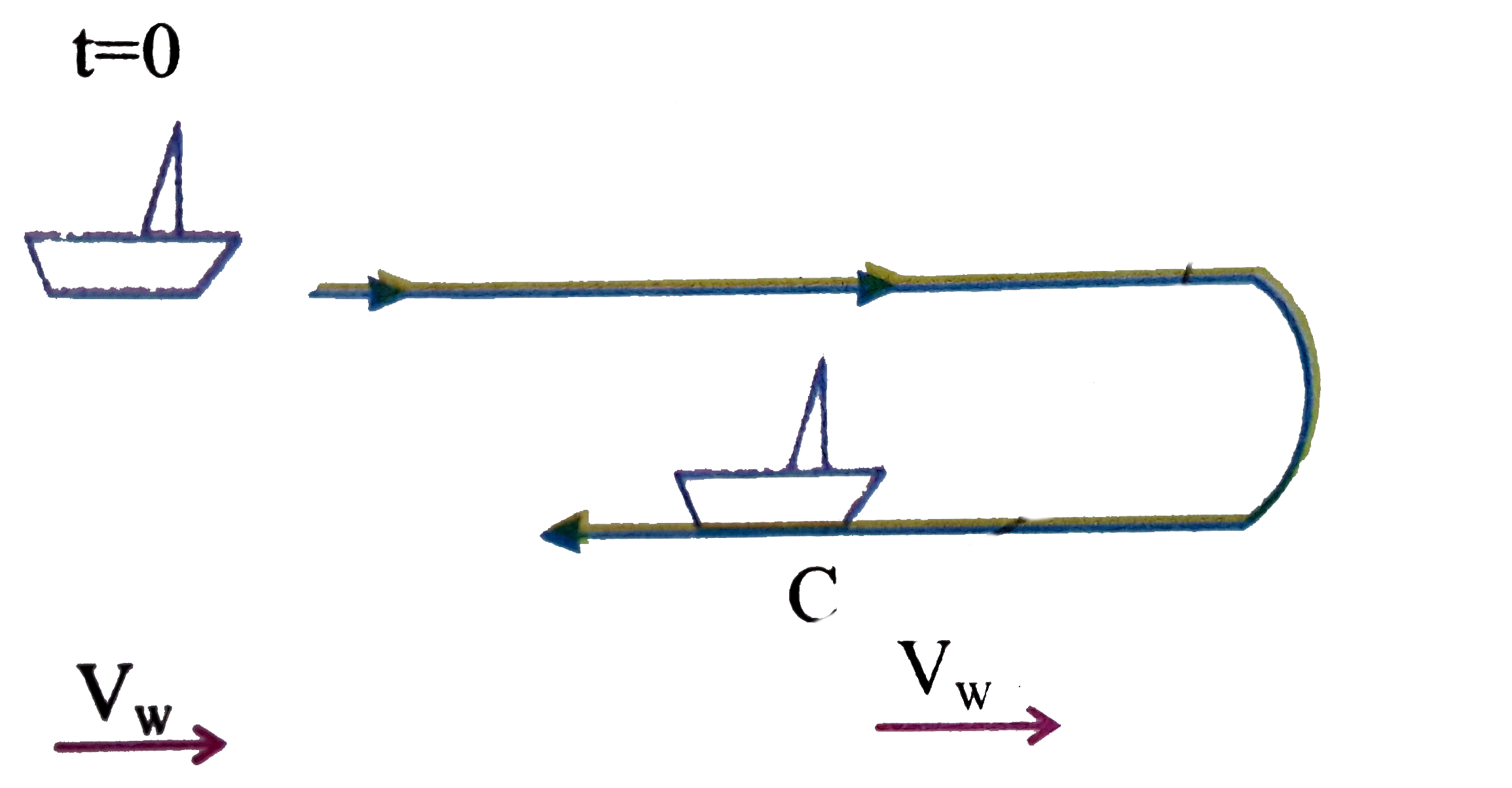
View SolutionA boat is moving with a velocity vbw=5km/hr relative to water. At time t=0.the boat passes through a piece of cork floating in water while moving down stream.If it turns back at time t1=30min.
a) when the boat meet the cork again?
b) The distance travelled by the boat during this time.
View SolutionA man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
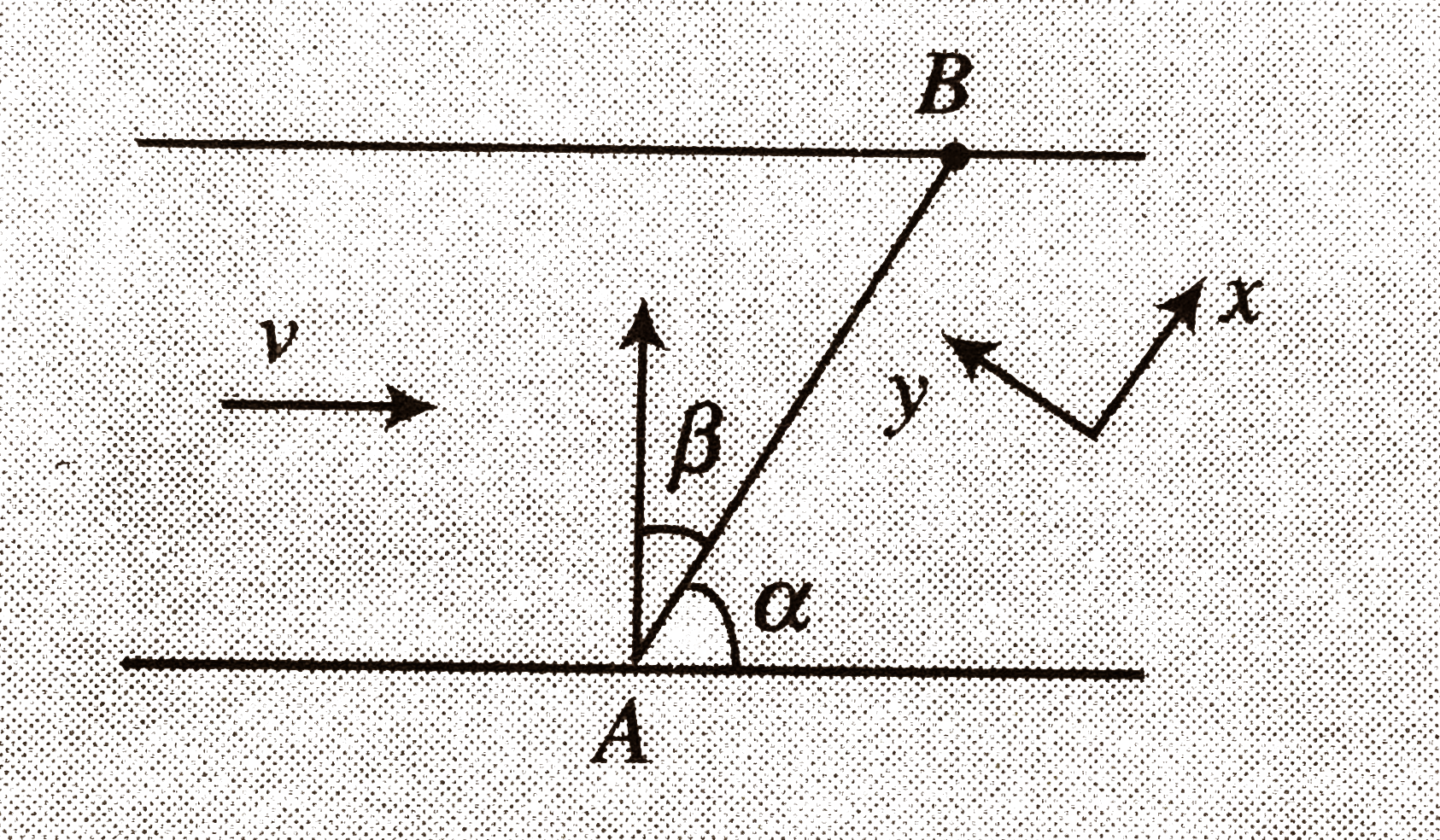 .
.
View Solution
