A swimmer wants to cross a 200 m wide river which is flowing at a speed of 2 m/s. the velocity of the swimmer with respect to the river is 1 m/s. how far from the point directly opposite to the starting point does the swimmer reach the opposite bank ?
200 m
400 m
600 m
800 m
The correct Answer is:B
To solve the problem of how far the swimmer reaches from the point directly opposite to the starting point, we can follow these steps:
1. Identify the Given Data:
- Width of the river (D) = 200 m
- Velocity of the river (Vr) = 2 m/s
- Velocity of the swimmer with respect to the river (Vs) = 1 m/s
2. Calculate the Time Taken to Cross the River:
The time (t) taken by the swimmer to cross the river can be calculated using the formula:
t=DVs
Substituting the values:
t=200 m1 m/s=200 seconds
3. Calculate the Distance Drifted Downstream:
While the swimmer is crossing the river, the river is also flowing downstream. The distance (d) drifted downstream can be calculated using the formula:
d=Vr×t
Substituting the values:
d=2 m/s×200 seconds=400 m
4. Conclusion:
The swimmer reaches a point 400 m downstream from the point directly opposite to the starting point.
Final Answer:
The swimmer reaches the opposite bank 400 meters downstream from the point directly opposite to the starting point.
---
- Width of the river (D) = 200 m
- Velocity of the river (Vr) = 2 m/s
- Velocity of the swimmer with respect to the river (Vs) = 1 m/s
The time (t) taken by the swimmer to cross the river can be calculated using the formula:
t=DVs
Substituting the values:
t=200 m1 m/s=200 seconds
While the swimmer is crossing the river, the river is also flowing downstream. The distance (d) drifted downstream can be calculated using the formula:
d=Vr×t
Substituting the values:
d=2 m/s×200 seconds=400 m
The swimmer reaches a point 400 m downstream from the point directly opposite to the starting point.
The swimmer reaches the opposite bank 400 meters downstream from the point directly opposite to the starting point.
Similar Questions
A 400m wide river is flowing at a rate of 2.0ms−1. A boat is sailing with a velocity of 10ms−1 with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View SolutionVelocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View SolutionA river 400m wide is flowing at a rate of 2.0m/s. A boat is sailing at a velocity of 10.0m/s with respect to the water In a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
View SolutionA river is 20m wide. River speed is 3m/s. A boat starts with velocity 2√2m/s at angle 45∘ from the river current (relative to river)
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionA swimmer wishes to cross a 500m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View SolutionIf speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
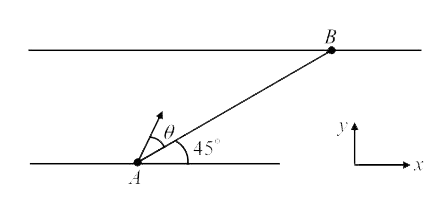
View SolutionA swimmer wants to directly reach the point B starting from A. The river is flowing along x-axis. If the velocity of the swimmer is √23 times the velocity of the river, find the angle θ from the line AB at which his swimming effort should be directed.
View Solution
