A table has three legs that are 1.00 m in length and a fourth leg that is longer by d - 0.50 mm, so that the table wobbles slightly. A steel cylinder with mass M = 290 kg is placed on the table (which has a mass much less than M) so that all four legs are compressed but unbuckled and the table is level but no longer wobbles. The legs are wooden cylinders with cross - sectional area A=1.0cm2, Young's modulus is E=1.3×1010N/m2. What are the magnitudes of the forces on the from the floor ?
We take the table plus steel cylinder as our system. The situation is like that in Fig. 12-1, except now we have a steel cylinder on the table. If the tabletop remains level, the legs must be compressed in the following ways : Each of the short legs must be compressed by the same amount (call it ΔL3) and thus by the same force of magnitude F3. The single long leg must be compressed by a larger amount ΔL4 and thus by a force with a larger magnitude F4. In other words, for a level tabletop, we must have
ΔL4=ΔL3+d.
From Eq. 12-3, we can relate a change in length to the force causing the change with ΔL=FL/AE, where L is the original length of a leg. We can use this relation to replace ΔL4 and ΔL3 in Eq. 12-6. However, note that we can approximate the original length L as being the same for all four legs.
Making those replacements and that approximation gives us
F4LAE=F3LAE+d.
We cannot solve this equation because it has two unknowns, F4 and F3.
To get a second containing F4 and F3, we can use a vertical y axis then write the balance of vertical forces (Fnet,y=0) as
3F3+F4−Mg=0,
where Mg is equal to the magnitude of the gravitational force of the system. (Three legs have force F3 on them.) To solve the simultaneous Eqs. 12-7 and 12-8 for, say, F3, we first use Eq, 12-8 to find that F4=Mg−3F3. Substituting that into Eq. 12-7 then yields, after some algebra,
F3=Mg4−dAE4L
=(290kg)(9.8m/s2)4
−(5.0×10−4m)(10−4m2)(1.3×1010N/m2)(4)(1.00m)
=548N≈5.5×102N.
From Eq. 12-8, we then find
F4=Mg−3F3=(290kg)(9.8m/s2)−3(548N)
≈1.2kN.
You can show that the three short legs are each compressed by 0.42 mm and the single leg by 0.92 mm.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PROBLEMS7videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - CHECKPOINT1videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)3videos
CURRENT AND RESISTANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )3videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
A uniform chain of length l and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
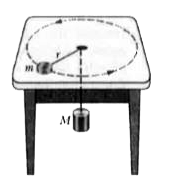
View SolutionA puck of mas m=1.50 kg slides in a circle of radius r=25.0 cm on a frictionless table while attached to a hanging cylinder of mass M=2.50 kg by means of a cord that extends through a hole in the table. What speed keeps the cylinder at rest?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36 - Question 2 - Select One
A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36 - Question 3 - Select One
A uniform chain of length l and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
A14mglB18mglC116mglD132mgl
A uniform chain of mass m and length l is placed on a smooth table so that one−third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?
 View Solution
View SolutionA uniform rope of length 3 m and mass 1 kg is kept on a table such that 80 cm of its length hangs freely from the edge of the table . Calculate the work done in pulling the entire rope on the table .
View SolutionA table has a heavy circular top of radius 1 m and mass 20 kg . It has four light legs of length 1 m fixed symmetrically on its circuference. What is the maximum weight which may be placed anywhere on this table wihtout toppling it?
View SolutionOne leg of a right triangle is 1 cm shorter than the other leg and the hypotenuse is 2cm longer than the longer leg . What is the length of the longer leg ?
View SolutionA metal cuboid of mass M kg rests on a table surface area of 40cm2 is in contact with the table the pressure exerted by the cuboid on the table surface is 10000Pa value of M is (given that,g=10ms−2)
View Solution

