
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
Let f be the force of friction between the shell and the horizontal surface
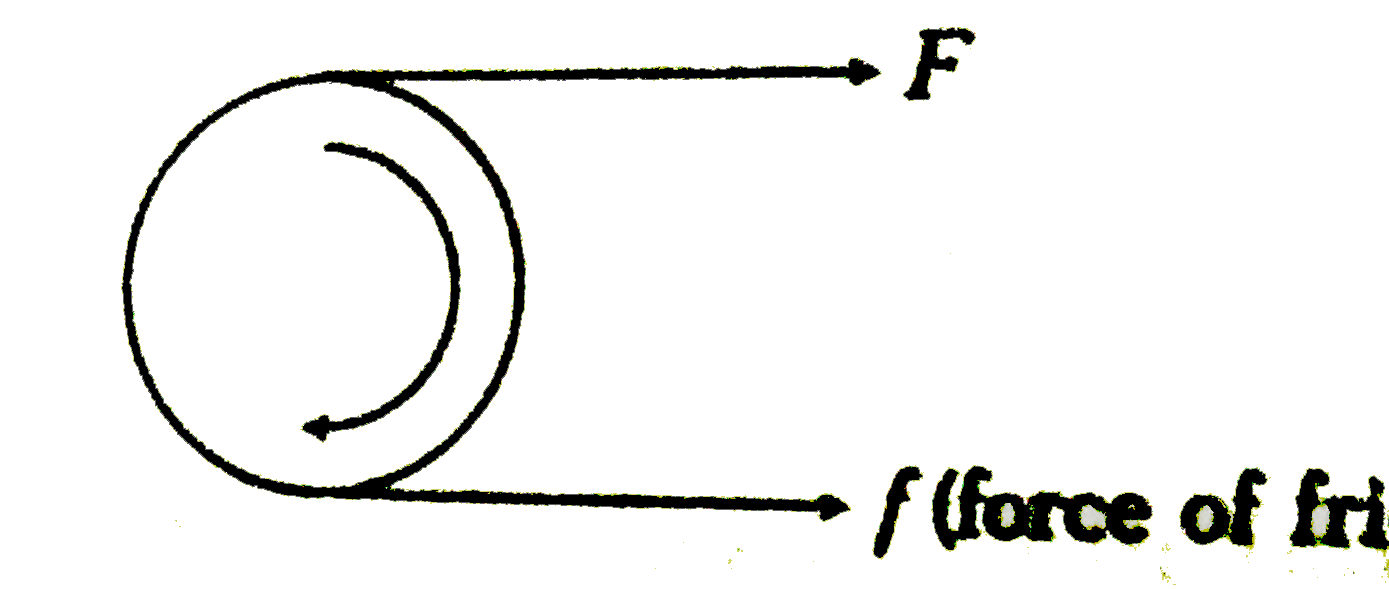
For translational motion
F+f=ma ….(i)
For rotational motion,
FR−fR=Iα=IaR(∵a=Rαfor pure rolling)
⇒F−f=IaR2...(ii)
Adding Eqs. (i) and (ii)
2F=(m+IR2)a=(m+23m)a=53ma
or F=56ma [∵Ishell=23mR2]
⇒a=6F5m.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A tangential force F acts at the top of a thin spherical shell of mass m and radius R as shown. Find the acceleration of the shell if it rolls without slipping. If your answer is αF5m. Then find α.
'(##CEN_KSR_PHY_JEE_C09_E01_030_Q17##)'
View SolutionA force F acts at the centre of a thin spherical shell of mass m and radius R.
Find the acceleration of the shell if the surface is smooth.
View Solution
Knowledge Check
Consider a thin spherical shell of uniform density of mass M and radius R:
AThe gravitational field inside the shell will be zeroBThe gravitational self energy of shell is GM22RCAttractive force experience by unit area of the shell pull the other half is GM22R2DNet gravitational force with which one hemisphere of the shell arracts other, is GM28R2A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
Athe particle will execute S.H.M inside the shellBthe particle will oscillate inside the shell, but the oscillations are not simple harmonicCthe particle will not oscillate, but the speed the particle will go on increasingDnone ot theseA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
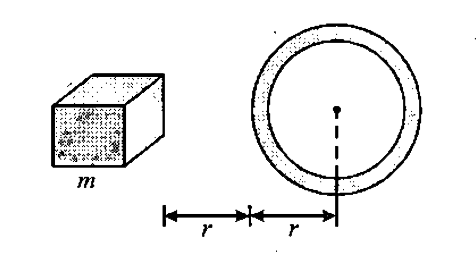 AOnly gravitational field inside the shell is zeroBGravitational field and gravitational potential both are zero inside the shellCGravitational potential as well as gravitational field inside the shell are not zeroDCan't be ascertained.
AOnly gravitational field inside the shell is zeroBGravitational field and gravitational potential both are zero inside the shellCGravitational potential as well as gravitational field inside the shell are not zeroDCan't be ascertained.
A tangential force 'F' is applied at the topmost point of a spherical shell of mass 'm' kept on a rough horizontal surface. If it rolls without slipping, it's acceleration is 6Fxm then 'x'
View SolutionA spherical shell of mass m and radius R is given then which of the following is incorrect for inside the sheel
View SolutionA horizontal force F acts at the centre of mass of a uniform disc with mass M and radius R. The maximum value of F for which the disc can roll without slipping is kμsMg. Find k. ( μ, is coefficient of friction)
View SolutionA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
View Solution
