A tank with a square base of area 2m2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20cm2 at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is (Takeg=10ms−2)
10N
20 N
40 N
80 N
The correct Answer is:C
The situation is as shown in the figure.
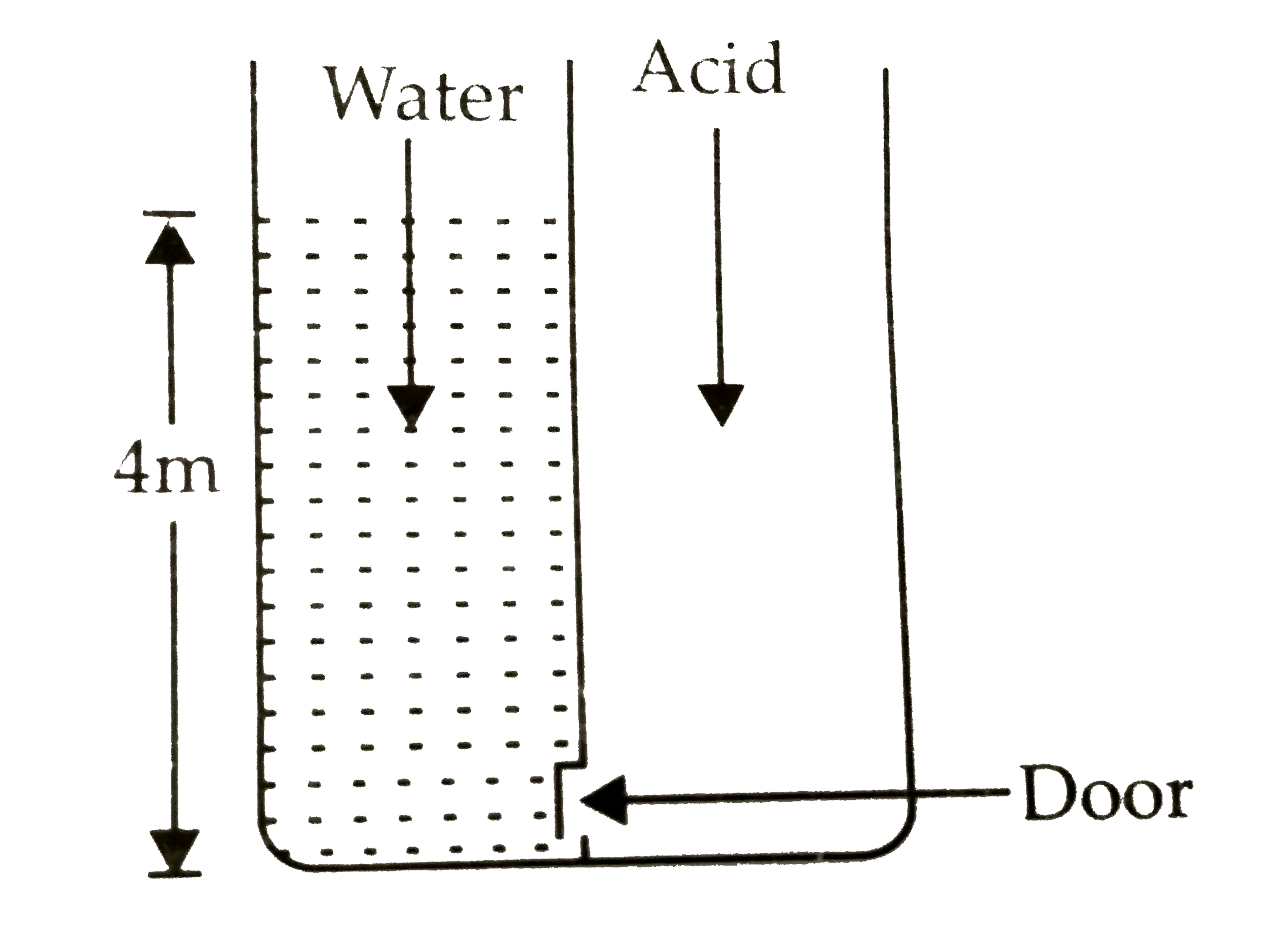
For compartment containing water,
h=4m,ρw=103kgm−3
Pressure exerted by the water at the door at the bottom is
Pw=ρwhg=103kgm−3×4m×10ms−2
=4×104Nm−2
For compartment containing acid,
ρa=1.5×103kgm−3,h=4m
Pressure exerted by the acid at the door at the bottom is
Pa=ρahg=1.5×103kgm3×4m×10ms−2
=6×104Nm−2
=6×104Nm−2
∴ Net pressure on the door =Pa−Pw
=(6×104−4×104)Nm−2=2×104Nm−2
Area of the door =20cm2=20×10−4m2
∴ Force on the door =2×104Nm−2×10−4m2
=40 N
Thus, to keep the door closed the force fo 40 N must be applied horizontally from the water side.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Streamline Flow
7 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Bernoulli'S Principle
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A tank with a square base of area 1.0m2 is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area 20cm2. The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of 4.0m. Compute to force necessary the force nec cessary to keep the door closed.
View SolutionA partition divides a container having insulated walls into two compartments I and II. The same gas fills the two compartment. What is the ratio of the number of molecules in compartments I and II ?

View Solution
Knowledge Check
A tank with a square base of area 2m2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20cm2 at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is (Takeg=10ms−2)
A10 NB20 NC40 ND80 NA box is divided into two equal compartments by a thin partition and they are filled with gases X and Y respectively. The two compartments have a pressure of 250 torr each. The pressure after removing the partition will be equal to:
A125 torrB500 torrC250 torrD750 torrThe level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
A10−2m3s−1B102m3s−1C10m3s−1D10−4m3s−1
The level of water in a tank is 5m high.A hole of area 1cm^2 is made in the bottom of the tank. The rate of leakage of water from the hole is (g=10ms^(-2)
View SolutionWater is being poured in a vessel at a constant rate αm2/s. There is a small hole of area a at the bottom of the tank. The maximum level of water in the vessel is proportional to
View SolutionA box of 1 L capacity is divided into two equal compartments by a thin partition which are filled with 2g H2 and 16 gCH4 respectively. The pressure in each compartment is reorded as P atm. The total pressure when partition is removed will be:
View SolutionThe door should be keep closed.
View SolutionIn Fig., a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. the lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. the heat capacities per mole of an ideal monoatomic gas are Cυ=32RandCP=52R, and those for an ideal diatomic gas are Cυe=52RandCP=72R.
Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. the total work done by the gases till the time they achieve equilibrium will be

View Solution
