(A) : The average magnitude of poynting vector $\to S$ is the intensity of electromagnetic wave. (R) : Poynting vector is given by $\to S = \frac{\to E \times \to B}{2 μ_{0}}$

A

Both 'A' and 'R' are true and 'R' is the correct explanation of 'A'.

B

Both 'A' and ’R' are true and 'R' is not the correct explanation of 'A

C

A' is true and 'R' is false

D

'A' is false and R' is true

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
- The assertion states that "The average magnitude of the Poynting vector $\to S$ is the intensity of an electromagnetic wave."
- The Poynting vector $\to S$ represents the power per unit area carried by an electromagnetic wave. The intensity $I$ of the wave is defined as the average power per unit area, which is indeed related to the average magnitude of the Poynting vector.
2. Understanding the Reason:
- The reason states that "The Poynting vector is given by $\to S = \frac{\to E \times \to B}{2 μ_{0}}$ ."
- The correct expression for the Poynting vector in terms of the electric field $\to E$ and the magnetic field $\to B$ is actually $\to S = \frac{\to E \times \to B}{μ_{0}}$ . The factor of $2$ in the denominator is incorrect.
3. Evaluating the Truth of Each Statement:
- Since the assertion is true (the average magnitude of the Poynting vector does represent the intensity of the electromagnetic wave) and the reason is false (the expression for the Poynting vector is incorrect), we conclude that:
- Assertion (A) is true.
- Reason (R) is false.
4. Final Conclusion:
- Therefore, the answer to the question is that the assertion is true but the reason is false.
Summary of the Answer:
- Assertion (A) is true.
- Reason (R) is false.
- The correct option is that A is true, but R is false.

|

Updated on:8/8/2024

Class 12 PHYSICS ELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The magnitude of the x-component of vector $\to A$ is 3 and the magnitude of vector $\to A$ is 5. What is the magnitude of the y-component of vector $\to A$ ?
A3
B4
C5
D8
Question 2 - Select One
An infinitely long thin wire carrying a uniform linear static charge density $λ$ is placed along the z-axis Fig. The wire is set into motion along its length with a uniform velocity $\to v = v ˆ k$ . Calculate the poynting vector $\to S = \frac{1}{μ_{0}} (\to E \times \to B)$ .

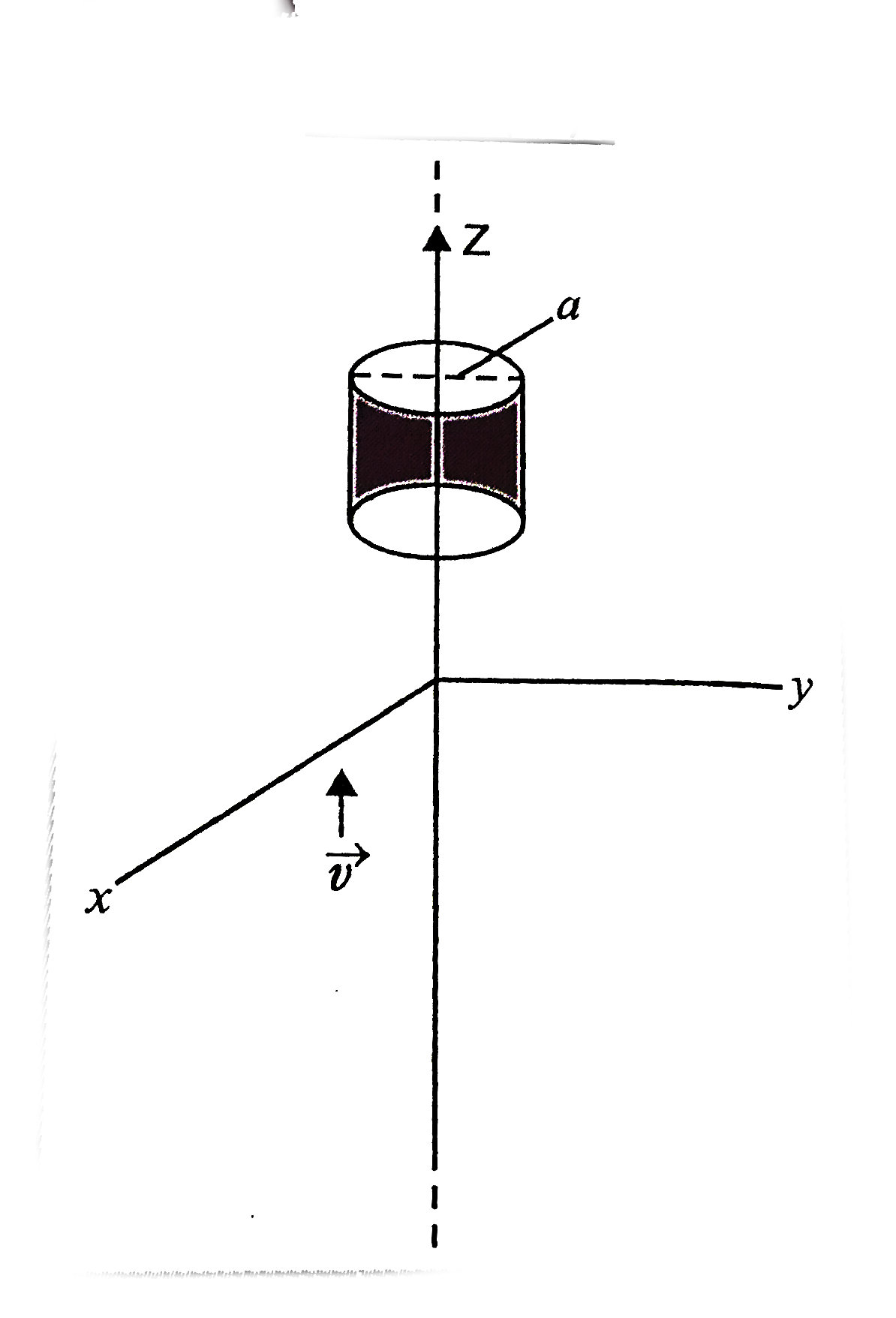A $\frac{- λ^{2} v}{4 π^{2} ε_{0} a^{2}} ˆ k$
B $\frac{λ^{2} v}{4 π^{2} ε_{0} a^{2}} ˆ i$
C $\frac{λ^{2} v}{4 π^{2} ε_{0} a^{2}} ˆ k$
D $\frac{- λ^{2} v}{4 π^{2} ε_{0} a^{2}} ˆ i$

AAKASH SERIES-ELECTROMAGNETIC WAVES-EXERCISE -IB

Home
Ask Doubt
Profile