(a) The motion of the particle in simple harmonic motion is given by x=asinωt. If its speed is u, when the displacement is x1 and speed is v, when the displacement is x2, show that the amplitude of the motion is
A=[v2x21−u2x22v2−u2]1/2
(b) A particle is moving with simple harmonic motion is a straight line. When the distance of the particle from the equilibrium position has the values x1 and x2 the corresponding values of velocity are u1 and u2, show that the period is
T=2π[x22−x21u21−u22]1/2
The correct Answer is:A
(a) u=ω√A2−x21 …(i)
v=ω√A2−x22 …(ii)
Solving Eqs. (i) and (ii), we get the result,
Aora=√v2x21−u2x22v2−u2
(b) u1=ω√A2−x21 ...(iii)
u2=ω√A2−x22 ...(iv)
Solving Eqs. (iii) and (iv), we find
ω=
⎷u21−u32x22−x21=2πT
∴T=2π
⎷x22−x21u21−u22 .
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A particle executing harmonic motion is having velocities v1 and v2 at distances is x1 and x2 from the equilibrium position. The amplitude of the motion is
View SolutionThe displacement of a particle performing simple harmonic motion is given by, x=8sinωt + 6 cos ωt, where distance is in cm and time is in second. What is the amplitude of motion?
View Solution
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2πThe displacement of a particle executing simple harmonic motion is given by
x=3sin(2πt+π4)
where x is in metres and t is in seconds. The amplitude and maximum speed of the particle isA3m, 2πms−1B3m, 4πms−1C3m, 6πms−1D3m, 8πms−1
A particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is
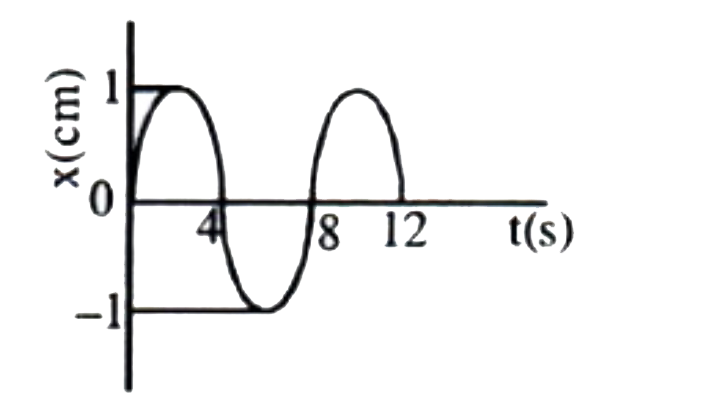
View SolutionA particle starts performing simple harmonic motion. Its amplitude is A. At one time its speed is half that of the maximum speed. At this moment the displacement is
View SolutionThe displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
View SolutionMaximum speed of a particle in simple harmonic motion is vmax. Then average speed of this particle in one time period is equal to
View SolutionTwo simple harmonic motions given by, x=asin(ωt+δ) and y=asin(ωt+δ+π2) act on a particle will be
View Solution
