A thin bar of mass m and length l is free to rotate about a fixed horizontal axis through a point at its end.The bar is brought to a horizontal position. (θ=90∘) and then released. The angular velocity when it reaches the lowest point is
(a)directly proportional to its length and inversely proportional to its mass
(b)independent of mass and inversely proportional to the square root of its length
(c)dependent only upon the acceleration due to gravity and the mass of the bar
(d)directly proportional to its length and inversely proportional to its length and inversely proportional to the acceleration due to gravity.
The correct Answer is:B
To solve the problem of finding the angular velocity of a thin bar of mass m and length l when it reaches the lowest point after being released from a horizontal position, we can follow these steps:
Step 1: Understand the Energy Conservation Principle
When the bar is released from the horizontal position, it converts its potential energy into rotational kinetic energy as it swings down to the vertical position.
Step 2: Calculate the Initial Potential Energy
The initial potential energy (PE_initial) of the bar when it is horizontal can be calculated using the formula:
PEinitial=mgh
where h is the height of the center of mass above the lowest point. Since the center of mass of the bar is at a distance of l2 from the pivot point, we have:
h=l2
Thus,
PEinitial=mg(l2)=mgl2
Step 3: Calculate the Final Rotational Kinetic Energy
The rotational kinetic energy (KE_final) of the bar when it reaches the lowest point is given by:
KEfinal=12Iω2
where I is the moment of inertia of the bar about the pivot point (end of the bar). The moment of inertia of a thin rod about an axis through one end is:
I=13ml2
Therefore,
KEfinal=12(13ml2)ω2=ml2ω26
Step 4: Apply Conservation of Energy
According to the conservation of energy, the initial potential energy is equal to the final kinetic energy:
PEinitial=KEfinal
Substituting the expressions we found:
mgl2=ml2ω26
Step 5: Simplify and Solve for Angular Velocity
We can cancel m from both sides (assuming m≠0):
gl2=l2ω26
Now, multiply both sides by 6:
3gl=l2ω2
Dividing both sides by l2:
ω2=3gl
Taking the square root of both sides gives:
ω=√3gl
Final Answer
Thus, the angular velocity ω when the bar reaches the lowest point is:
ω=√3gl
---
When the bar is released from the horizontal position, it converts its potential energy into rotational kinetic energy as it swings down to the vertical position.
The initial potential energy (PE_initial) of the bar when it is horizontal can be calculated using the formula:
PEinitial=mgh
where h is the height of the center of mass above the lowest point. Since the center of mass of the bar is at a distance of l2 from the pivot point, we have:
h=l2
Thus,
PEinitial=mg(l2)=mgl2
The rotational kinetic energy (KE_final) of the bar when it reaches the lowest point is given by:
KEfinal=12Iω2
where I is the moment of inertia of the bar about the pivot point (end of the bar). The moment of inertia of a thin rod about an axis through one end is:
I=13ml2
Therefore,
KEfinal=12(13ml2)ω2=ml2ω26
According to the conservation of energy, the initial potential energy is equal to the final kinetic energy:
PEinitial=KEfinal
Substituting the expressions we found:
mgl2=ml2ω26
We can cancel m from both sides (assuming m≠0):
gl2=l2ω26
Now, multiply both sides by 6:
3gl=l2ω2
Dividing both sides by l2:
ω2=3gl
Taking the square root of both sides gives:
ω=√3gl
Thus, the angular velocity ω when the bar reaches the lowest point is:
ω=√3gl
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionA thin rod of mass m and length l is free to rotate on a smooth horizontal plane about its one fixed end. When it is at rest, it receives a horizontal impulse J at its other end, at angle of 37∘ with the length. Choose incorrect option immediately after impact:
View SolutionA uniform rod of mass M and length L, which is free to rotate about a fixed vertical axis through O, is lying on a frictionless horizontal table. A particle of equal mass strikes the rod with a velocity V0 and sticks to it. The angular velocity of the combination immediately after the collision is:
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
View SolutionAn L shaped thin uniform rod of total length 2l is free to rotate in a vertical plane about a horizontal axis a P as shown in the figure. The bas is released from rest. Neglect air and contact friction. The angular velociyt at the instant it has rotated through 90∘ and reached the dotted position shown is
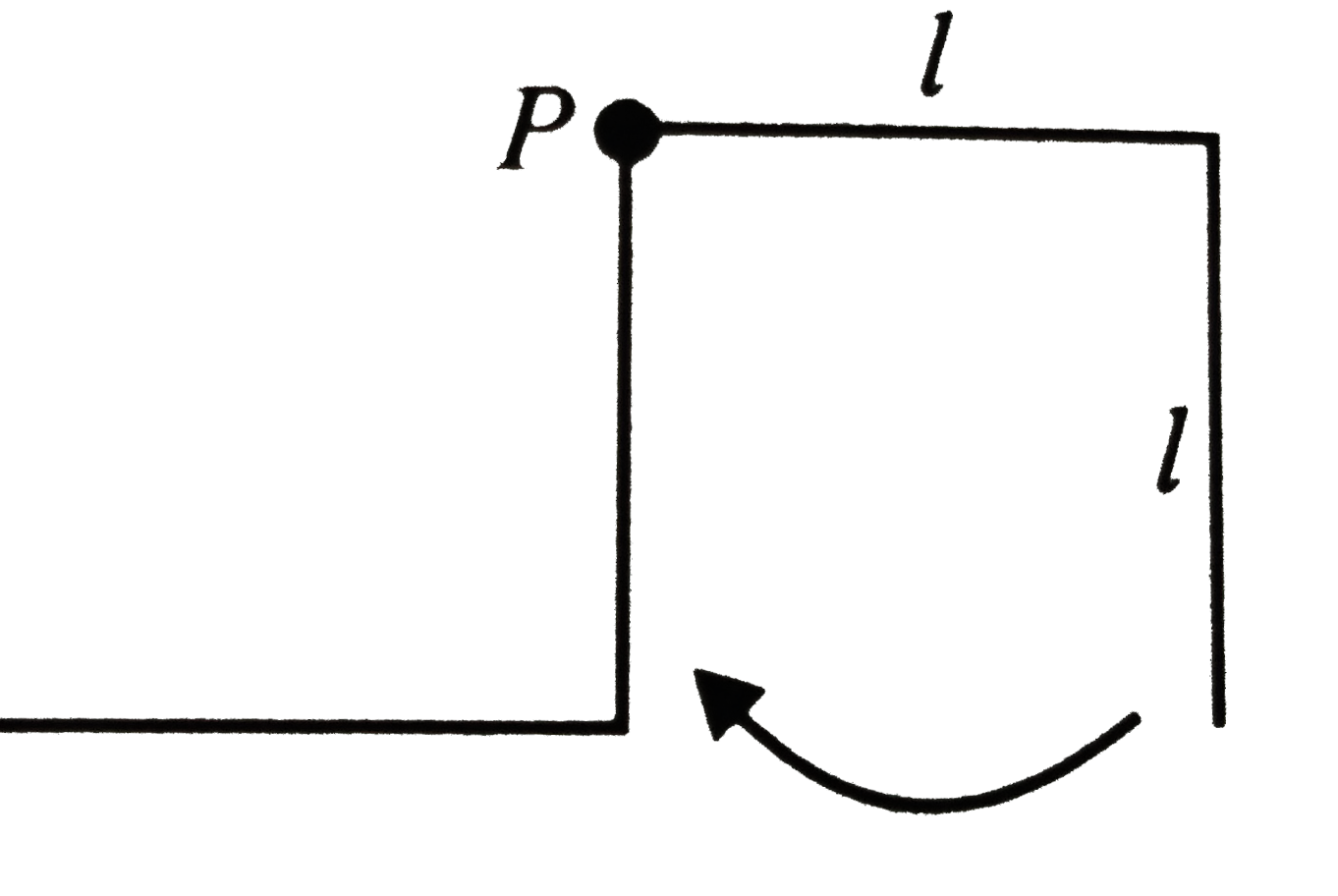
View Solution
