A thin plate of large area is placed midway in a gap of height h filled with oil of viscosity and the plate is pulled at constant velocity vby applying the same drag force on the plate. If a lighter oil of viscosity η is then substituted in the gap. it is found that for the velocity v, and the same drag force as previous case the plate is located unsymmetrically in the gap but parallel to the walls. Find η in terms of distance from nearer wall to the plane y.
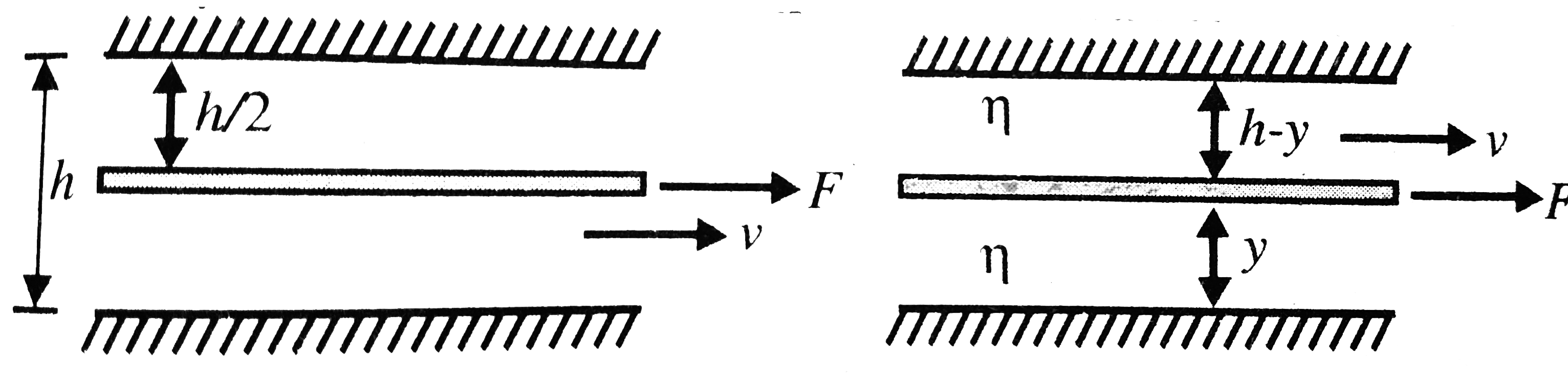
The correct Answer is:(1−yh)
Case I:
Drag force F1+F2
[η0vh/2+η0vh/2]A
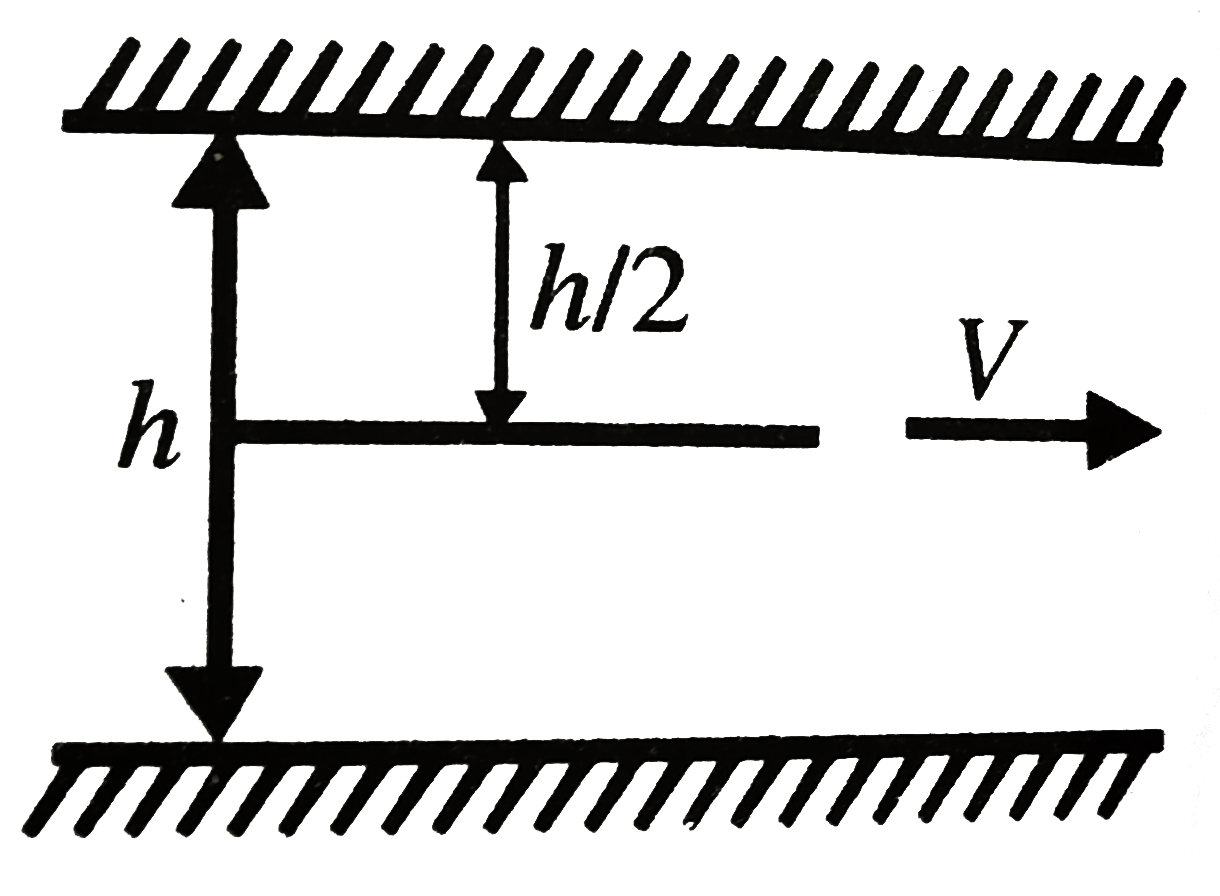
Case II:
Drag force on the plane
=[η−vh−y+ηvy]A=ηvhay(h−y)
In both cases drag force are equal
⇒4η0vAh=ηvhay(h−a)
⇒η=4η0h(1−yh)
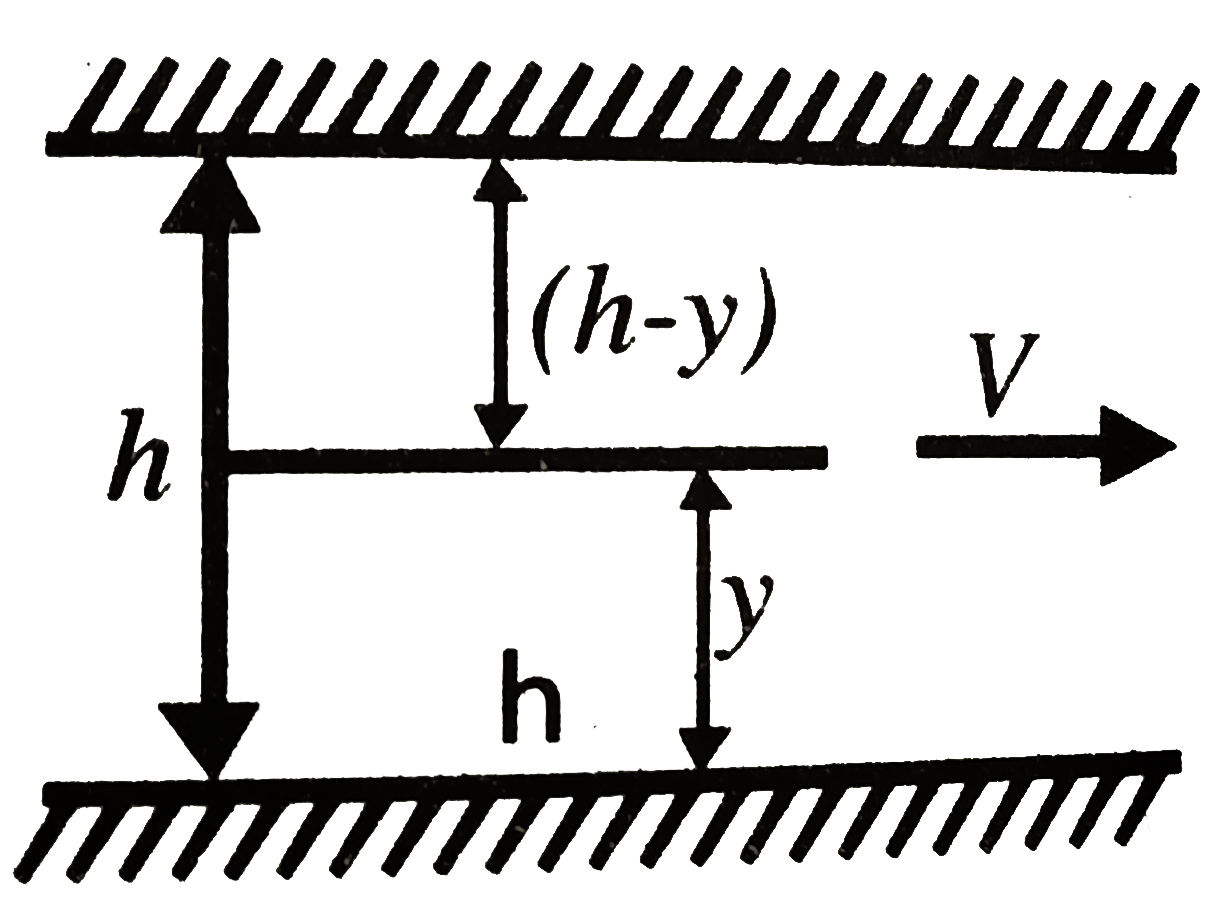
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Single Correct
112 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct
17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.3
9 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water of viscosity η0and the plate has a constant velocity v by applying a force F as shown in the figure. If the gap is filled with some other liquid of viscosity 0.75η0 at what minimum distance (in cm) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity V. by applying the same force F? (Take h=20cm)

View SolutionViscosity| Viscous & drag force on flat plate| Stoke's law: terminal velocity
View Solution
Knowledge Check
A drop of water of radius r is falling rhough the air of coefficient of viscosity η with a constant velocity of v the resultant force on the drop is
A16πηrvB6πηrvC√6πηrvDzeroIf the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
AIncreases by a factor 2BIncreases by a factor √2CDecreased by a factor √2DDecreased by a factor 1/2An oil drop of mass m and falls through a medium that offers a viscous drag force. F. if the velocity of the drop is constant it means that
AF>mgBF<mgCF>mgDF=mg
A metal plate of area 10−3m2 is placed on a liquid layer of thickness 0.8mm . The coefficient of viscosity of that liquid is 24poise.Then the horizontal force required to move the plate with a velocity of 1cms−1.
View SolutionA plate of area 100cm2 is placed on the upper surface of castor oil, 2mm thick. Taking the coefficient of viscosity to be 15.5 poise, calculate the horizontal force neccesary to move the plate with a velocity 3cm−1.
View SolutionIf Q is the charge on the pates of a capacitor of capacitances C,V the potential difference between the plates, s the area of each plate and d the distance between the plates, the force of attraction between the plates is-
View SolutionA large drop of oil whose density is less than that of water, floats up through a column of water assume that the oil an the water do not mix. The coefficient of viscosity of the oil is η∘ and that of water is ηW the velocity of the drop will depend on
View SolutionA parallel plate capacitor was lowered into water in a horizontal position, with water filling up the gap between the plates. The distance between the plates is d. Then a constant voltage V was applied to the capacitor. Find the water pressure increment in the gap. Dielectric constant of water is k.
View Solution
