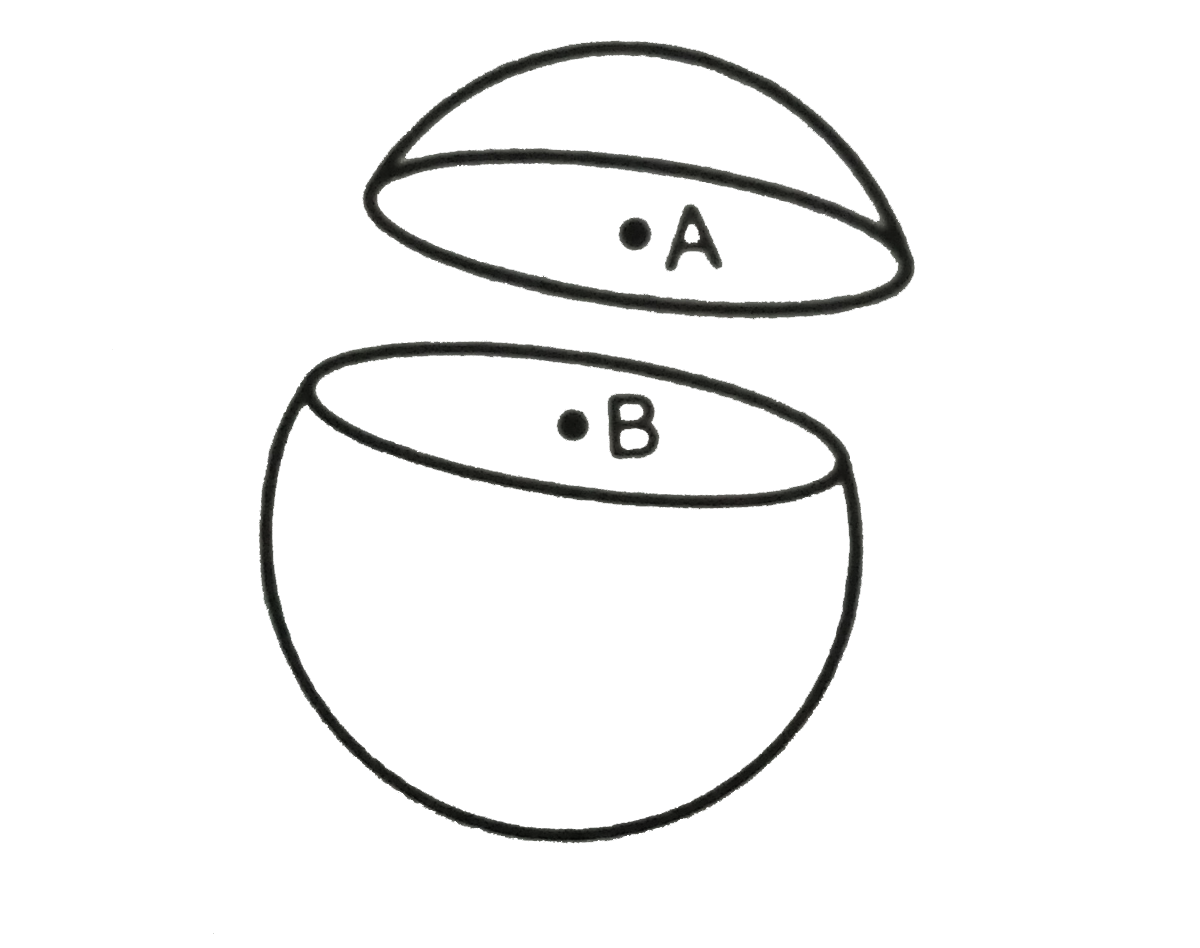
A thin sphereical shel having uniform density is cut in two parts by as palne and kept separated as shown in figure. The point A is the centre of the plane section of the first par and B is the centre of the plane sectioin of the second part Show that the grvitationas field at A due to teh first part ss equal in magnitude to the gravitational field at B due to the second part.
The correct Answer is:A
We know in the thin sphereical shell of uniform density has gravitatioiN/Asl field at its interN/Al point is zero at A and B points, field is equal and opposite and canel each other. So Net field is zero.
Hence, EA=EB
Topper's Solved these Questions
Similar Questions
Knowledge Check
A current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
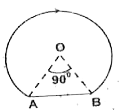 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the ratio of the volumes of the upper part and the cone is given by
A1:4B1:8C1:6D1:12If a cone is cut into two parts by a horizontal plane passing through the mid point of its axis , the ratio of the volumes of the upper part and the frustum is :
A1:1B1:2C1:3D1:7
If a cone is cut into two parts by a horizontal plane passing through the mid point of its axis , the ratio of the volumes of the upper part and the frustum is :
View SolutionIf a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, then the ratio of the volumes of the upper part and the given cone is
View Solution94 Is divided Into two parts in such a way that the fifth part of the first and the eighth part of the second are in the ratio 3:4. The first part is :
View Solution94 Is divided Into two parts in such a way that the fifth part of the first and the eighth part of the second are in the ratio 3:4. The first part is :
View SolutionA solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.

View Solution
