A thin spherical conducting shell of radius $r_{1}$ carries a charge $Q$ . Concentric with it is another thin metallic spherical shell of radius $r_{2} (r_{2} > r_{1})$ . Calculate electric field at distance $r$ when (i) $r < r_{1}$ ,(ii) $r_{1} < r < r_{2}$ and (iii) $r > r_{2}$ .
What will be the field in above cases if outer shell $(a)$ is given charge $q$ and $(b)$ is earthed ?

Text Solution

Verified by Experts

We know that electric field inside a conductor is zero and for external point , whole charge is assumed to be concentrated at centre. 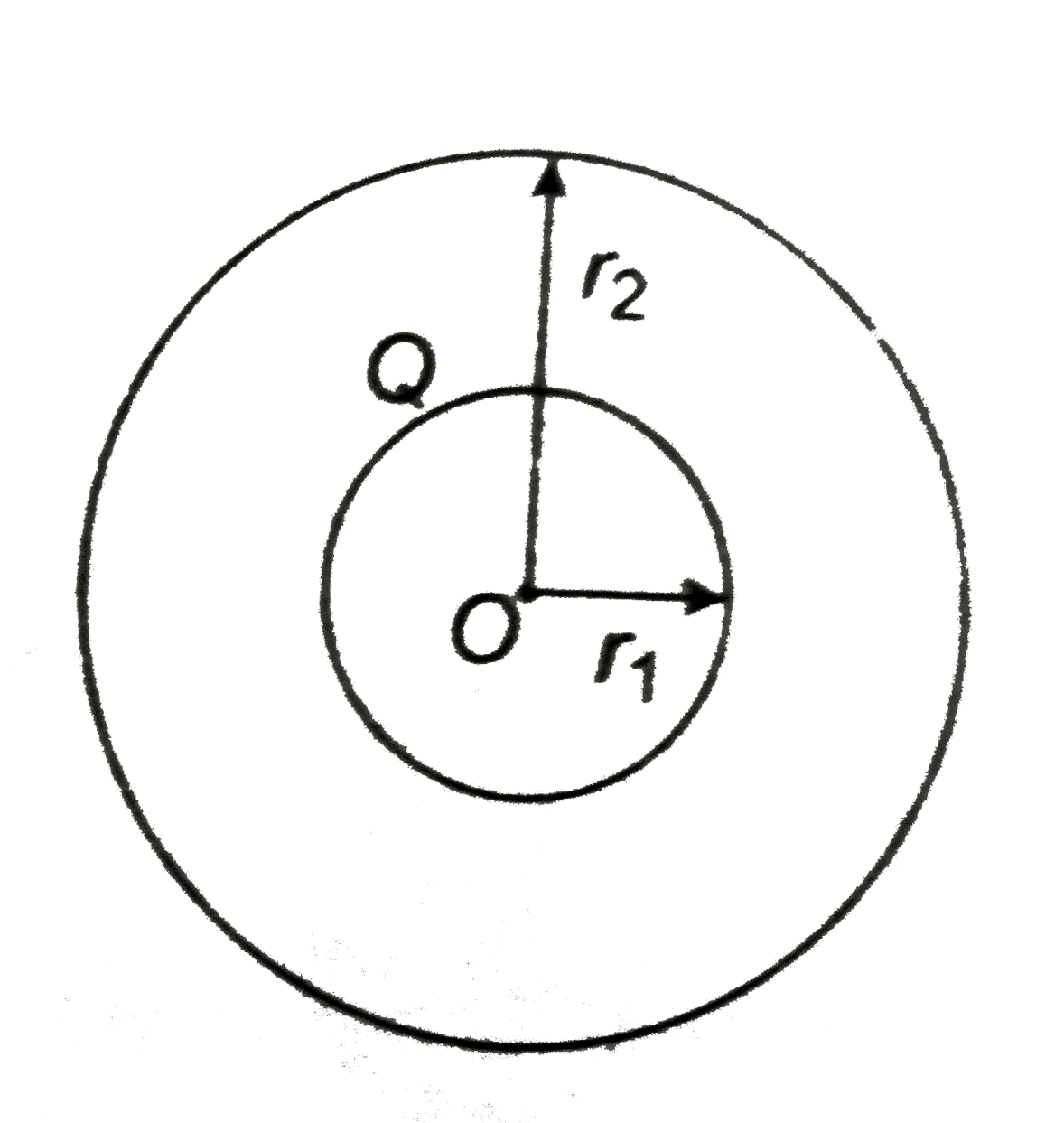(i) $r < r_{1}, E = 0$
(ii) $r_{1} < r < r_{2}, E = \frac{1}{4 π \in_{0}} \frac{Q}{r^{2}}$
(iii) $r > r_{2}, E = \frac{1}{4 π \in_{0}} \frac{Q}{r^{2}}$
(a)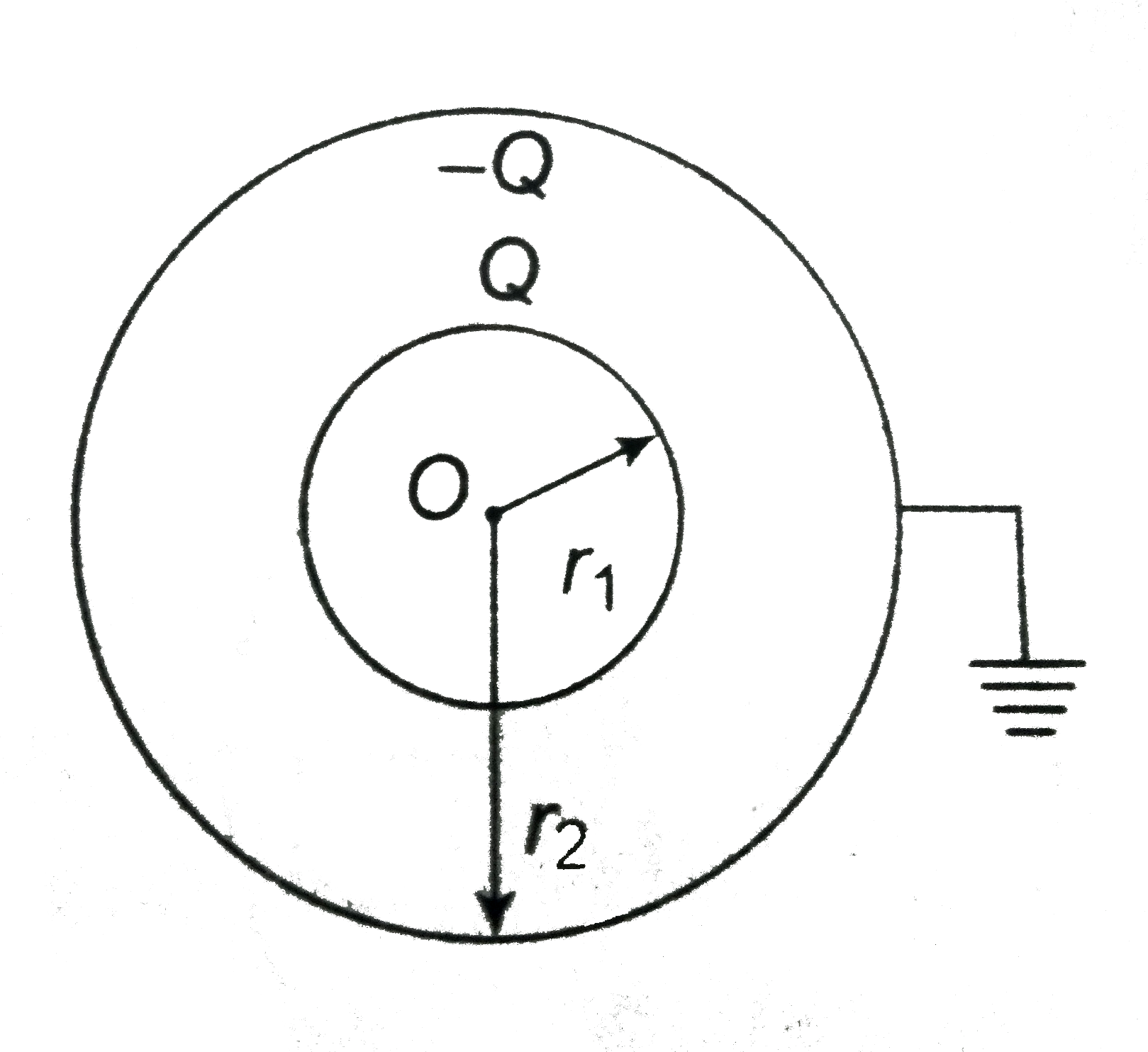
(i) $r < r_{1}, E = 0$
(ii) $r_{1} < r < r_{2}, E = \frac{1}{4 π \in_{0}} \frac{Q}{r^{2}}$
(iii) $r > r_{2}, E = \frac{1}{4 π \in_{0}} \frac{(Q + q)}{r^{2}}$
(b)
(i) $r < r_{1}, E_{0}$
(ii) $r_{1} < r < r_{2}, E = \frac{1}{4 π \in_{0}} \frac{Q}{r^{2}}$
(iii) Due to eathing , charge on inner surface on outer shell is $- Q$ . Therefore,
$r > r_{2}, E = 0$

Updated on:21/07/2023