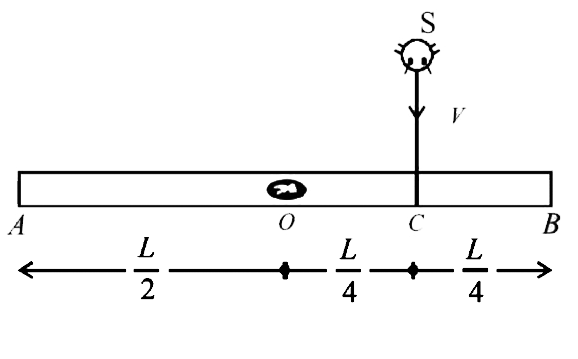
A thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length √3meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
The correct Answer is:B
Initial Kinetic Energy
=12m1v21+12m2v22+12MV2
=120.08×102+120.08×62_0=5.44J…(i)
Applying law of conservation of linear momentum during
collision
m1×v1+m2×v2=(M+m1+m2)Vc
where vc is the velocity on it after collision
0.08×10+0.08×6=(0.16+0.08+0.08)vc
⇒Vc=4ms
∴ Translational kinetic energy after collision
=12(M+m1+m2)V2c=2.56J...(ii)
Applying conservation of angular momentum of the bar
and two particle system about the centre of the bar.
Since extrnal torque is zero, the inital angular momentum
is equal to final angular momentum.
Initial angular momentum
=m1v1×x−m2v2x
=0.08×10x0.5−0.08×6×0.5
=0.4−0.24=0.16kgm2s−1 (in clockwise direction)<br>F∈alanga––rmomentum= I omega<br>=[(Ml^2)/(12) + m_1x^2+m_2x^2]omega<br>=[((0.16)(sqrt3)^2/(12 + 0.08xx(0.5)^2 + (0.08)(0.5)^2]omega<br>=0.08 omega<br>:. 0.08 omega = 0.16 rArr omega =2rad/s ...(iii)
The rotational kinetic energy
=Translational K.E. + Rotational K.E.
= 2.56+0.16 = 2.72 J
The change in K.E. = Initial K.E.- Final K.E.
=5.44 - 2.72 = 2.72J
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Video
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
A thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is 0.16 kg and lengths is √3m. Two particles, each of mass 0.08kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10ms−1 and the other with 6ms−1, as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distance 0.5 m from the centre of the bar. The particles strike the bar at same instant of time and stick to the bar on collision. Calculate the loss of kinetic energy of the system in the above collision process.

View SolutionA stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?

View Solution
Knowledge Check
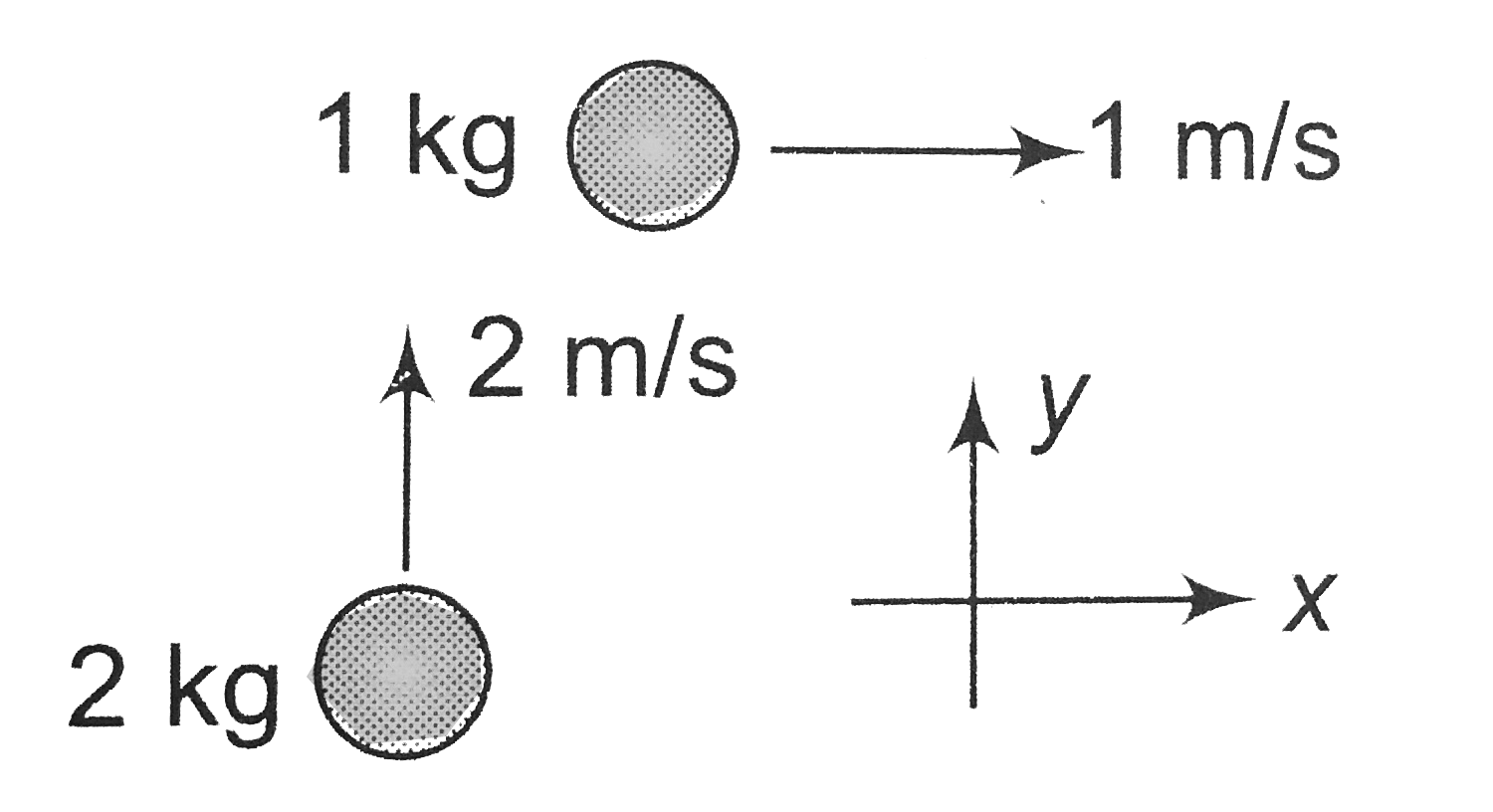
Two bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
 A3m/sB1.67m/sC1.5m/sD1.37m/s
A3m/sB1.67m/sC1.5m/sD1.37m/sA stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?
 Am=2MBm=MCm=M/2Dm=M/4
Am=2MBm=MCm=M/2Dm=M/4Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
A103m/sB107m/sC112m/sD123m/s
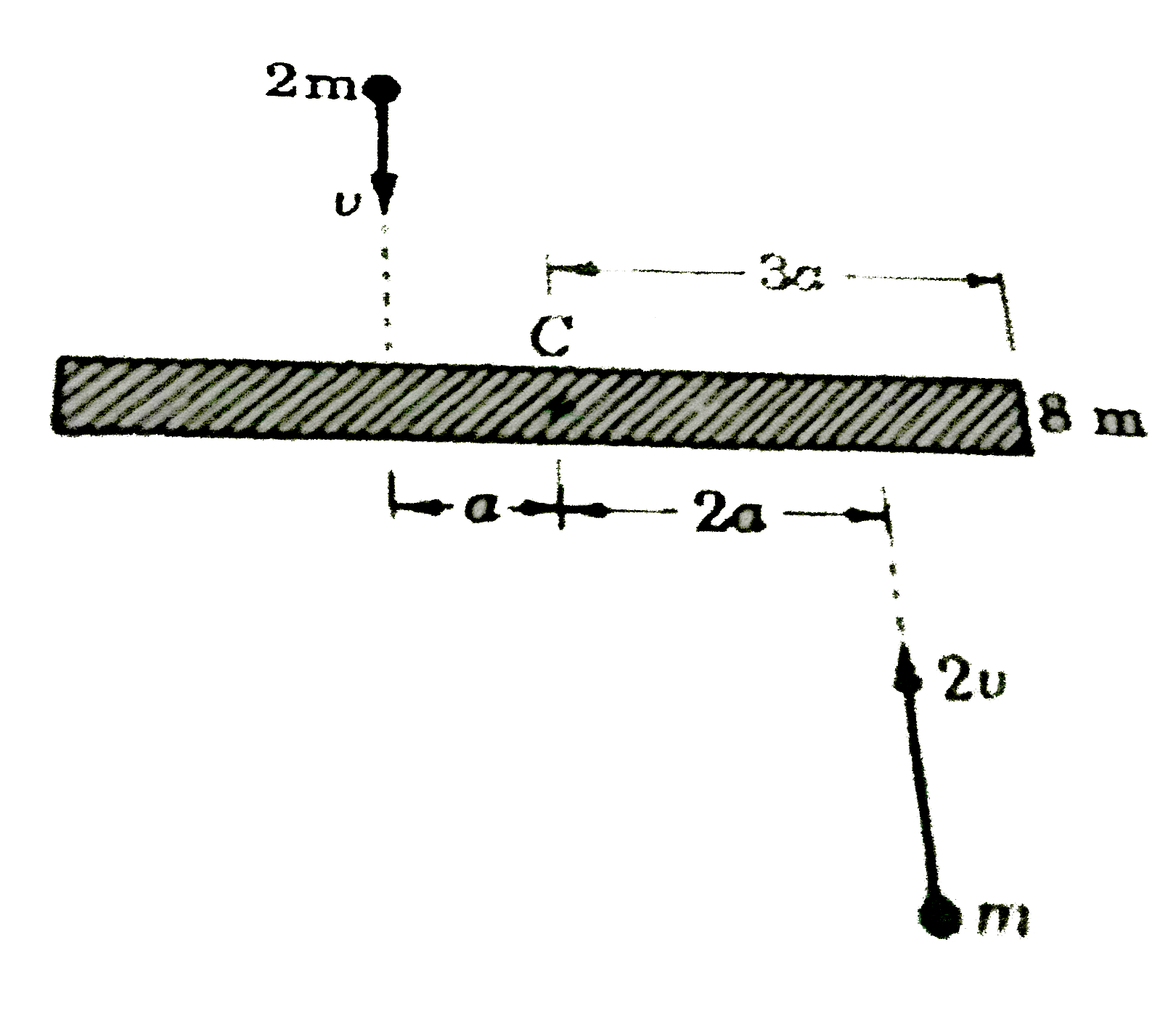
A uniform bar of length 6a and mass 8 m lies on a smooth horizontal table. Two point-masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively strike the bar as shown in Fig, and stick to the bar after collision.
View Solution0A body of mass 20 kg moving with a velocity of 3 m/s, rebounds on a wall with same velocity. The impulse on the body is -
View SolutionTwo smooth spheres A and B of masses 4kg and 8kg move with velocities 9m/s and 3m/s in opposite directions. If A rebounds on its path with velocity 1m/s, then
View SolutionTwo bodies having same mass 40 kg are moving in opposite direction. One with a velocity of 10 m/s and the other will 7m/s. if they collide nd move as one body, the velocity of the combination is
View SolutionIn the figure shown A and B are free to move . All the surface are smooth. Mass of Aism. Then
View Solution