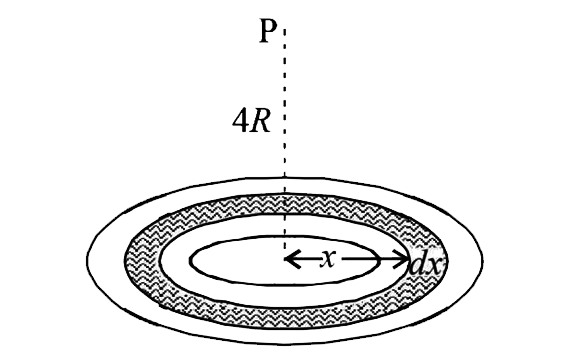
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

A

$\frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

B

$- \frac{2 G M}{7 R} (4 \sqrt{-} 5)$

C

$\frac{G M}{4 R}$

D

$\frac{2 G M}{5 R} (\sqrt{2} - 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

(a) Let us consider a circular elemental area of radius x and
thickness dx. The area of the sheded portion $= 2 π x d x .$
Let dm be the mass of the shaded portion
$: \frac{M a s s}{a r e a} = \frac{M}{π (4 R^{2}) - π {(3 R)}^{2}}$
$= \frac{d m}{2 π x d x} j$
$∴ D m = \frac{2 M}{7 R^{2}} x d x$
The gravitational potential of the mass dm at P is
$d V = \frac{- G d m}{{\sqrt{4 R}}^{2} + x^{2} = - \frac{G}{\sqrt{16} R^{2} + x^{2}} \times \frac{2 M}{7 R^{2}} x d x}$
$= \frac{- 2 G M}{7 R^{2}}$ (xdx)/(sqrt16R^2 + x^2) $(1)$
Suppose $16 R^{2} + x^{2} = t^{2}$
$\Rightarrow 2 x d x = 2 t d t \Rightarrow x d x = t d t$
Also for $x = 3 R, t = 5 R$
and for $x = 4 R, t = 4 \sqrt{2} R$
On intefrating equation (1), taking the above limits,
we get
$V = - \int_{5 R}^{4 \sqrt{2} R} \frac{2 G M}{7 R^{2}} d t = \frac{- 2 G M}{7 R^{2}} {[t]}_{5 R}^{4 \sqrt{2} R}$
$= \frac{- 2 G M}{7 R^{2}} [4 \sqrt{2} R - 5 R] \Rightarrow V = \frac{- 2 G M}{7 R} (4 \sqrt{2} - 5)$
$N o w \frac{W_{P} \infty}{1} = V_{\infty} - V_{P} = - V_{P} [∴ V_{\infty} = 0]$
$∴ W_{P \infty} = \frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219videos
HEAT AND THERMODYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
The energy required to move a body of mass $m$ from an orbit of radius $3 R$ to $4 R$ is
A $\frac{G M m}{2 R}$
B $\frac{G M m}{6 R}$
C $\frac{G M m}{12 R}$
D $\frac{G M m}{24 R}$
Question 2 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zero
Bfield is zero but potential is $\frac{G M}{R}$
Cfield is zero but potential is $- G M / R$
Dmagnitude of field is $\frac{G M}{R^{2}}$ and potential $- \frac{G M}{R}$
Question 3 - Select One or More
A thin annular disc of outer radius R and $\frac{R}{2}$ inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity $ω$ . Choose the correct option(s):
AThe magnetic field intensity at the centre of the disc is $\frac{μ_{0} Q ω}{3 π R}$
BThe magnetic field intensity at the centre of the disc is $\frac{μ_{0} Q ω}{4 R}$
CThe magnetic moment of the disc is $\frac{5 Q ω R^{2}}{16}$
DThe magnetic moment of the disc is $\frac{3 Q ω R^{2}}{4}$

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-GRAVITATION-JEE Main And Advanced

Home
Ask Doubt
Profile