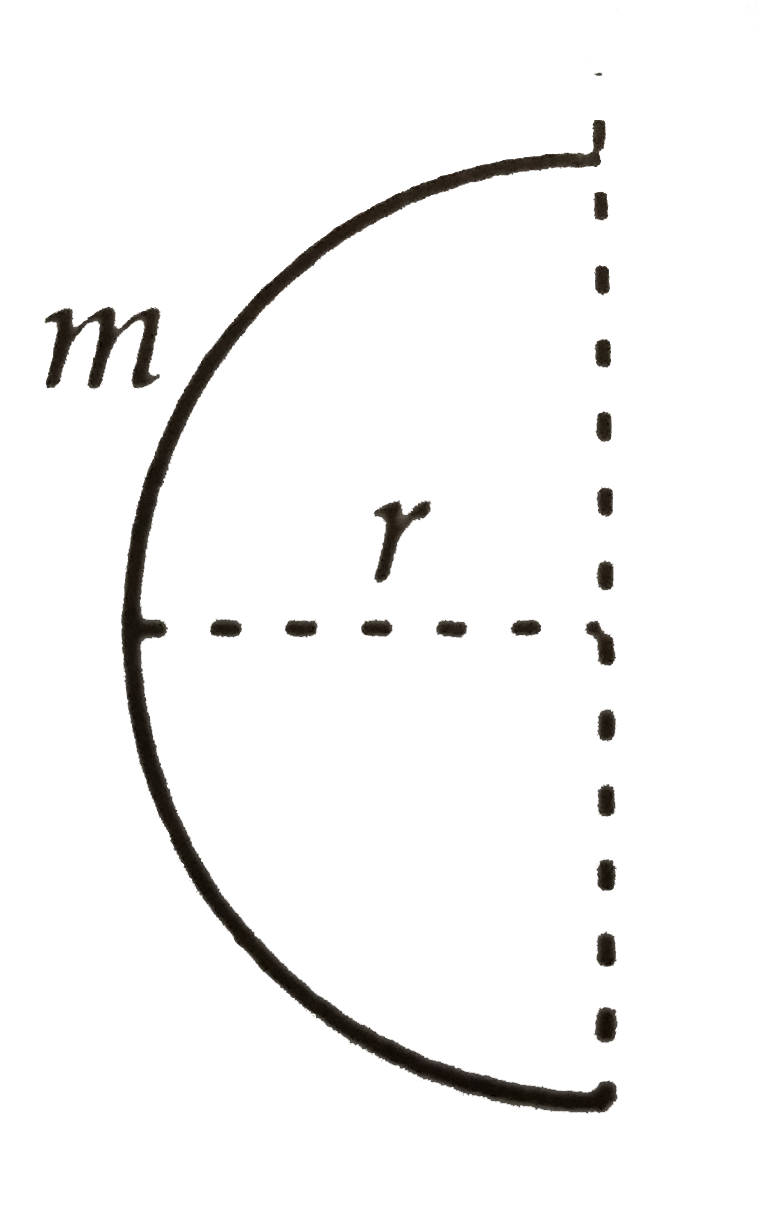
A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
ml2
zero
ml2/2π2
ml2/2π2
The correct Answer is:C
Given that, length of wire
= Perimeter of semicircle
or, πr=l
∴ r=1π
Moment of inertia of a right about its diameter =12mr2
∴ Moment of inertia of semicircle
=12[m(1π)2]=ml22π2
Topper's Solved these Questions
Similar Questions
A uniform wire of length l and mass M is bent in the shape of a semicircle of radius r as shown in figure. Calculate moment of intertia about the axis XX'
View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View Solution
Knowledge Check
A thin wire of length l and mass m is turned into the form of a semicircle. Its moment of inertia about an axis joining its free ends will be
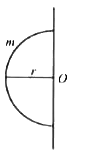 Amπl2Bml2/π2Cml22πDml22π2
Amπl2Bml2/π2Cml22πDml22π2A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 AMl22BMl2π2C2Ml2π2DMl22π2
AMl22BMl2π2C2Ml2π2DMl22π2An iron rod of length L and magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be
AMB2MπCMπDMπ

A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View SolutionA wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is
View SolutionA wire of mass 'm' and length 'l' is bent in the form of a circular ring. The moment of inertia of the ring about its axis is-
View SolutionA wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
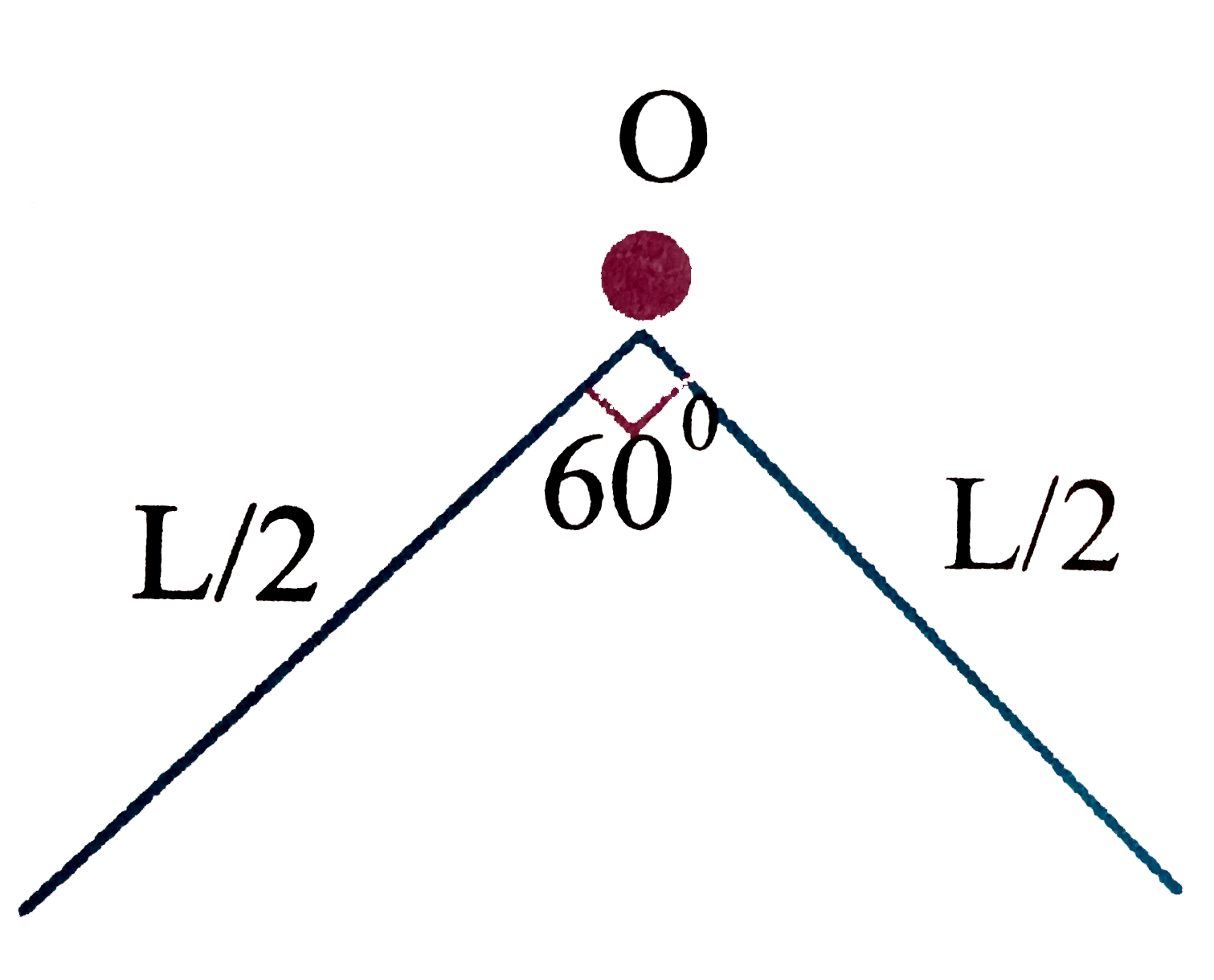
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
View Solution
