A threaded rod with 12turns/cm and diameter 1.18cm is mounted horizontally. A bar with a threaded hole to match the rod is screwed onto the rod. The bar spins at 216rev/min. How long will it take for the bar to move 1.50cm along the rod ?
As the distance between two consecutive threads on the rod, i.e., pitch is =(1/12) cm, so the number of rotations to be made in moving a distance of 1.5cm.
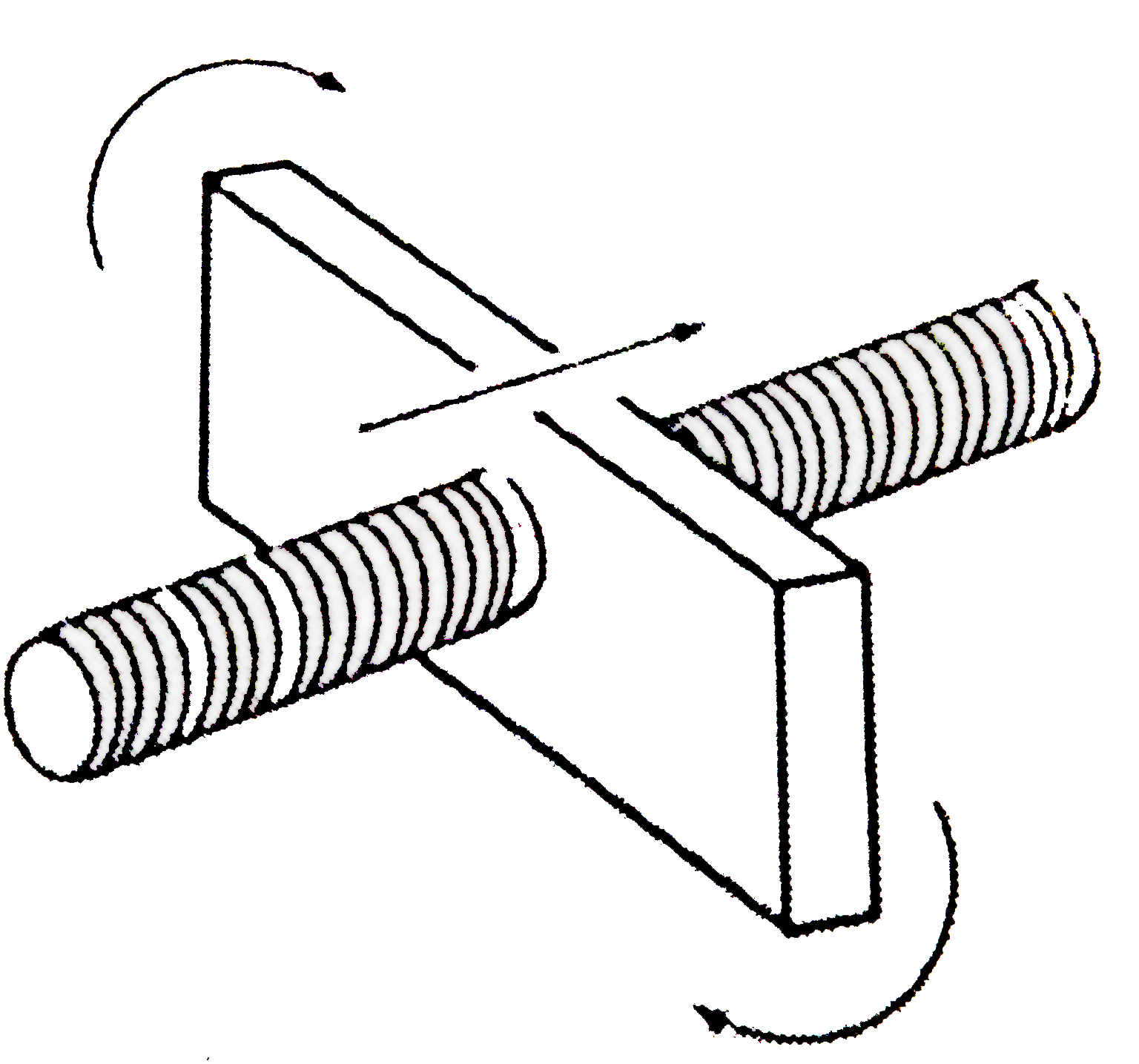
n=distancepitch=1.5(1/12)=18
So, angu lar displacement of bar
θ=2πn=2π×18=36π rad
And as angu lar speed of bar
ω=2πnt=2π×21660
=7.2 π rad/s So, time taken by bar to travel a distance of 1.5 cm on the rod (as θ=ωt with α=0)
t=θω=36π7.2π=5s
Topper's Solved these Questions
Similar Questions
A threaded rod with 12turns/cm and diameter 1.18cm is mounted horizontal. A bar with a threaded hole to match the rod is screwed onto the rod. The bar spins at 216rev/min. How long will it take for the bar to move 1.50cm along the rod ?
View SolutionIn the arrangement shown in fig the mass of the ball 1 is η=1.8 times as great as that of rod 2 The length of the later is l=100 cm The masses of the pulleys and the threads as well as the friction are negligible The ball is set on the same level as the lower end of the rod and then released How soon will the ball be opposite to the other end of the rod
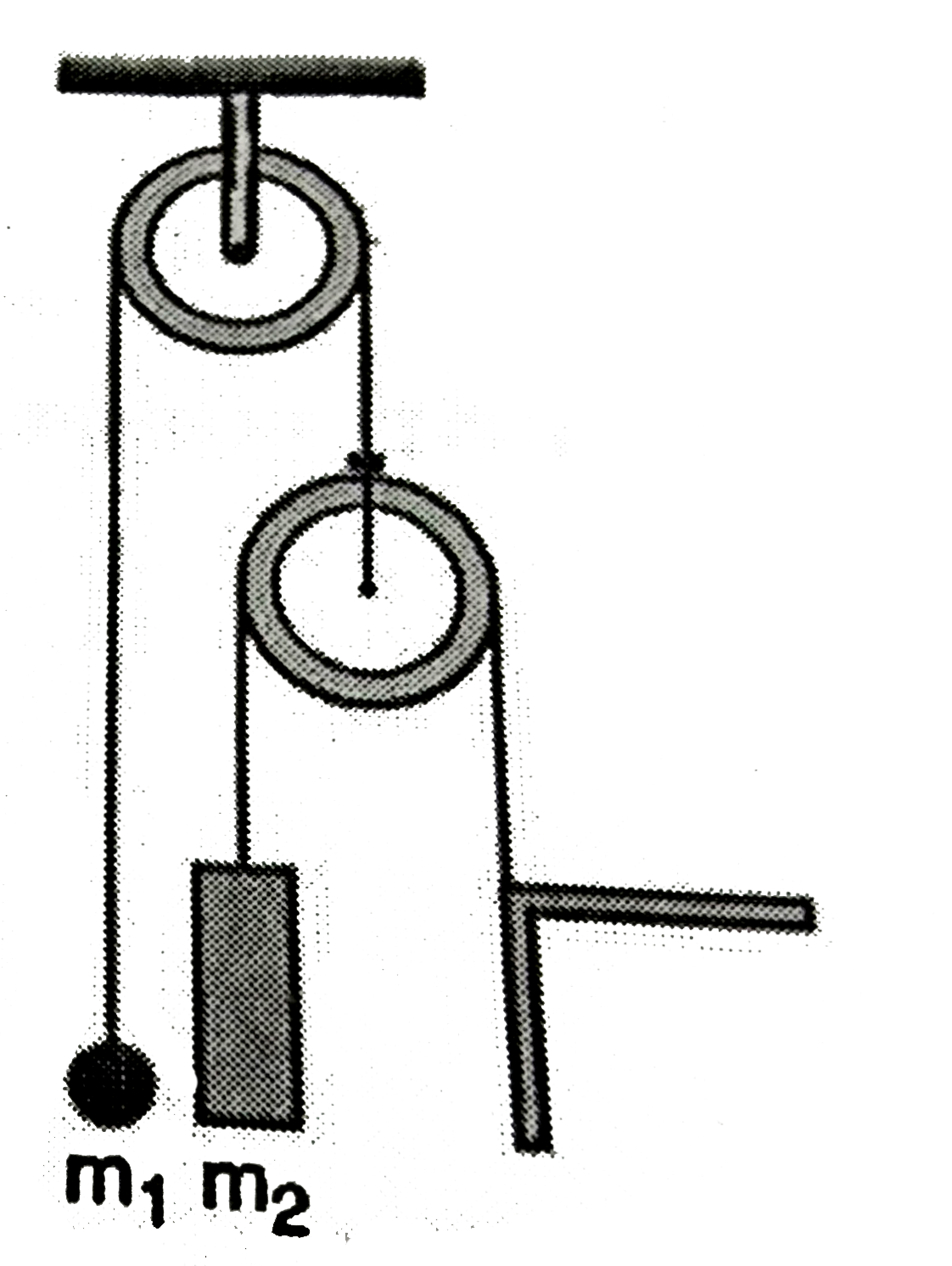
View Solution
Knowledge Check
An iron rod of length 20 cm and diameter 1 cm is placed inside a solenoid on which the number of turns is 600.The relative permeability of the rod is 1000.If a current of 0.5 A ios placed in the solenoid,then magnetisation of the rod will be
A2.997×102AmB2.9979×103AmC2.997×104AmD2.997×105AmA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.
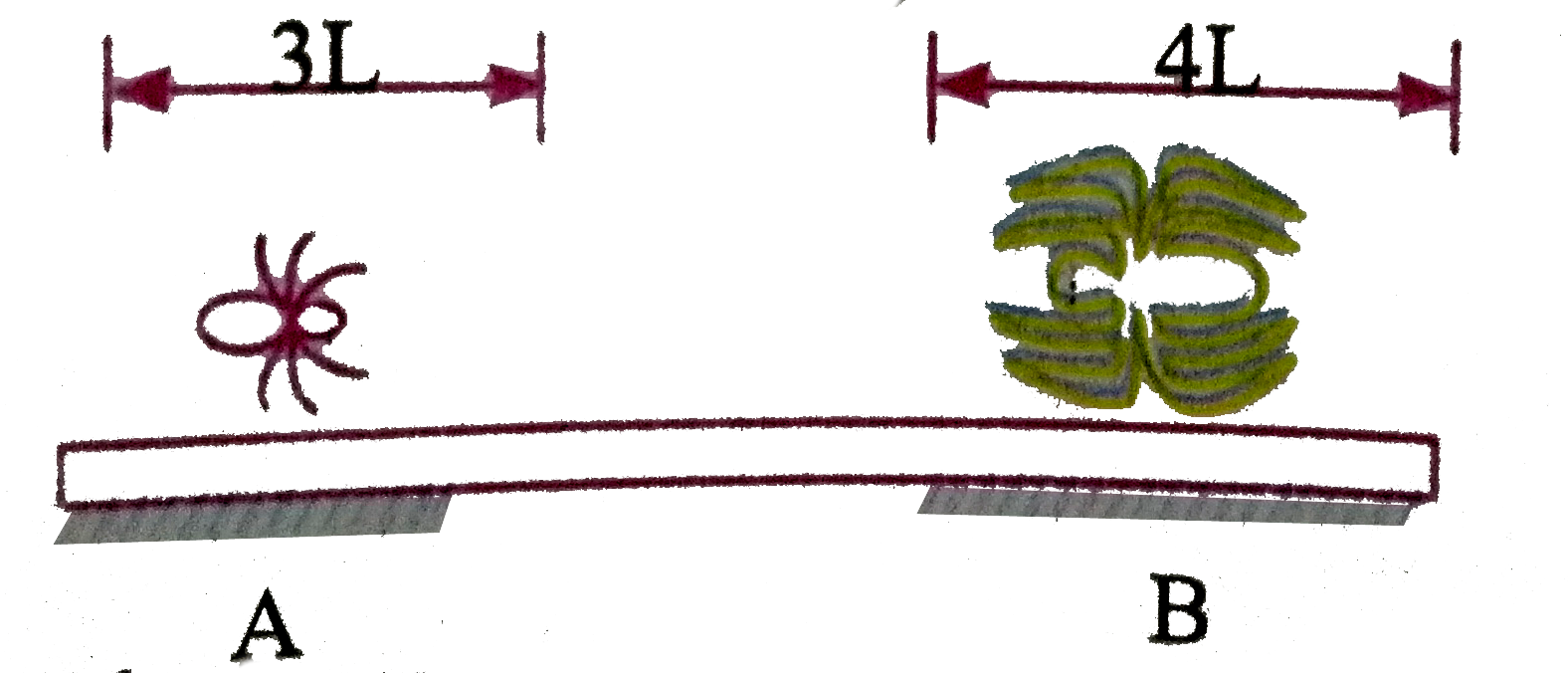
The speed of the bar after the spider eats up the moth and moves towards A isAv/2BvCv/6D2vA copper rod of 1 cm diameter and 8 cm length is drawn into a wire of uniform diameter and 18 m length. The raidus (in cm) of the wire is
A115B130C215D15
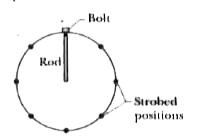
A bolt is threaded onto one end of a thin horizontal rod, and the rod is then rotated horizontally about its other end. An engineer monitors the motion by flashing a strobe lamp onto the rod and bolt, adjusting the strobe rate until the bolt appears to be in the same eight during each full rotation of the rod. The strobe rate is 2000 flashes per second, the bolt has mass 33 g and is at radius 4.0 cm. What is the magnitude of the force on the bolt from the rod?
View SolutionA brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250∘C, if the original lengths are at 40.0∘C? Is there a 'thermal stress' developed at the junction ? The ends of the rod are free to expand. Coefficient of linear expansion of brass =2.0×10−5.∘C−1 and that of steel =1.2×10−5.∘C−1.
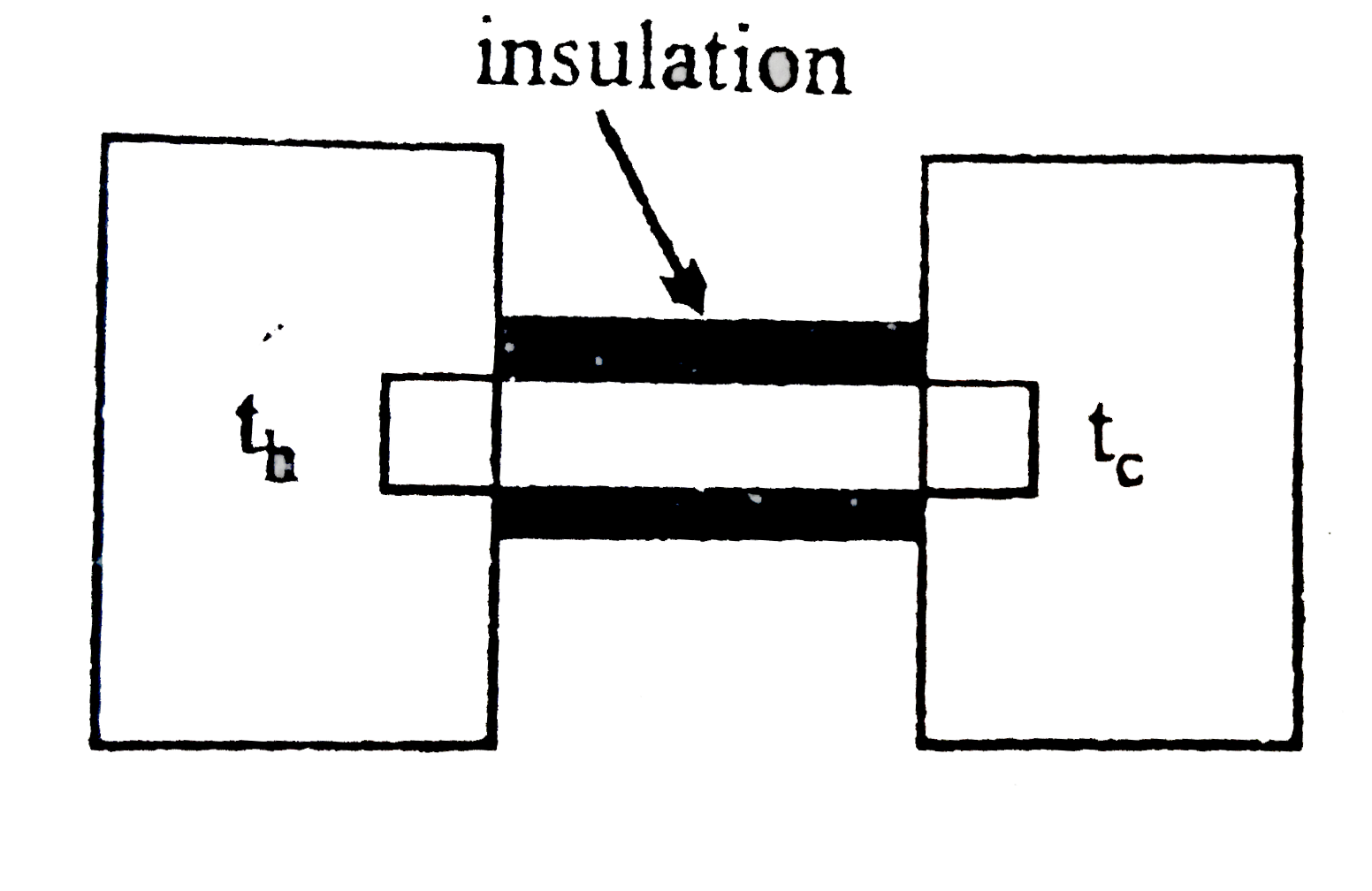
View SolutionAn insulated container is filled with a mixture of water and ice at tc=0∘C. Another container is filled with water that is continuously boiling at th=100∘C. In a series of experiments, the containers are connected by various thick rods that pass through the walls of the containers (see the diagram). The rod is insulated in such a way that there is no heat loss to surroundings. In experiment 1, a copper rod is used, and the ice melts in T1=2 min. In experiment 2, a steel rod of the same cross section is used, and the ice melts in T2=6 min. How long ( in min) would it take to melt the ice if the two rods are used "in series"?
View SolutionA copper rod of diameter 1 cm and length 8 cm is drawn in to a wire of length 18 m of uniform thickness. Find the thickness of wire.
View SolutionA copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
View Solution
