A track consists of two circular parts ABC and CDE of equal radius R and joined smoothly as shown. Each part subtends an angle 2θ at center. A vehicle of mass m travels with constant force by the road on the vehicle when it is at (i) B (ii) D (iii) just before C and (iv) just after C. (b) find the friction by the track on the vehicle when it is at B, C and D. (c) what should be the minimum friction coefficient between the road and the vehicle, which will ensure that cyclist can move with constant speed.

(a) At B: mg−NB=mv2R⇒NB=mg−mv2R
At D: ND−mg=mv2R⇒ND=mg+mv2R
just before C: mgcosθ−Nc=mv2R⇒Nc=mgcosθ−mv2R
Just after C: N'c−mgcosθ=mv2R
implies N'c=mgcosθ+mv2R
(b) since the vehicle is moving with constant speed, i.e., the tangential acceleration is zero, i.e., net tangential force on it always is zero.
At B and D, no component of weight along the surface of track, hence friction is not developed.
At C, component of weight mgsinθ is balancedby friction so that tangential force is zero, f=mgsinθ.
(c ) Just before C,f=μ1Nc, find μ1.
just after C,f=μ2N'c, find μ2.
since Nc<N'cμ>μ2.
Satisfy the requirement of μ1 as well as μ2, say μ1=0.80,μ2=0.60, minimum value of friction coefficient will be 0.80.

Topper's Solved these Questions
Similar Questions
A track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

View SolutionA track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

View Solution
Knowledge Check
An ant moves along a circular track of 6 m radius such that the arc of the circular track subtends an angle of 30∘ at the centre. The distance covered by the ant is
AπB13πC6πD4πIf the line segment joining the points A(a,b) and B(c,d) subtends an angle θ at the origin, then cosθ is equal to
Aab+cd√(a2+b2)(c2+d2)Bac+bd√(a2+b2)(c2+d2)Cac−bd√(a2+b2)(c2+d2)Dad+bc√(a2+c2)(b2+d2)
A vehicle is moving on a track with constant speed as shown in figure. The apparent weight of the vehicle is

View SolutionAn automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 ms2?
View SolutionAn automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 ms2?
View SolutionA wheel of radius 2.1 m of a vehicle makes
75 revolutions in one minute. What is the
speed of the vehicle ?
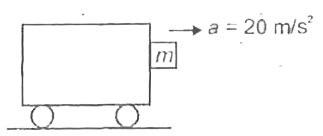
View SolutionA vehicle is moving on a road with an acceleration a=20m/s2 as shown in figure. The frictional coefficient between the block of mass (m) and the vehicle so that block is does not fall downward is (g=10m/s2)
View SolutionHow does a winding road makes it easier for vehicles to travel up a hill ?
View Solution
