A transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
To solve the problem step by step, we will follow these steps:
Step 1: Understand the given information
- Amplitude A=0.01m
- Frequency f=500Hz
- Displacement at x=0.1m is y(0.1)=−0.005m
- Displacement at x=0.2m is y(0.2)=+0.005m
Step 2: Write the general equation of the wave
The general equation for a transverse harmonic wave traveling in the positive x-direction is given by:
y(x,t)=Asin(ωt−kx)
Where:
- A is the amplitude
- ω is the angular frequency
- k is the wave number
Step 3: Calculate the angular frequency ω
The angular frequency ω can be calculated using the formula:
ω=2πf
Substituting the frequency:
ω=2π×500=1000πrad/s
Step 4: Set up equations using the given displacements
1. For x=0.1m:
−0.005=0.01sin(1000πt−k⋅0.1)
Simplifying gives:
−0.5=sin(1000πt−0.1k)(Equation 1)
2. For x=0.2m:
0.005=0.01sin(1000πt−k⋅0.2)
Simplifying gives:
0.5=sin(1000πt−0.2k)(Equation 2)
Step 5: Solve the equations for k
From Equation 1:
1000πt−0.1k=7π6(since sin7π6=−12)
From Equation 2:
1000πt−0.2k=π6(since sinπ6=12)
Step 6: Subtract the equations to eliminate t
Subtract Equation 2 from Equation 1:
(1000πt−0.1k)−(1000πt−0.2k)=7π6−π6
This simplifies to:
0.1k=6π6=π
Thus:
k=π0.1=10πrad/m
Step 7: Calculate the wavelength λ
The wave number k is related to the wavelength λ by:
k=2πλ
So:
λ=2πk=2π10π=0.2m
Step 8: Calculate the wave velocity v
The wave velocity v can be calculated using:
v=fλ
Substituting the values:
v=500×0.2=100m/s
Step 9: Write the final wave equation
Substituting A, ω, and k into the wave equation:
y(x,t)=0.01sin(1000πt−10πx)
Final Results
- Wavelength λ=0.2m
- Wave velocity v=100m/s
- Wave equation:
y(x,t)=0.01sin(1000πt−10πx)
- Amplitude A=0.01m
- Frequency f=500Hz
- Displacement at x=0.1m is y(0.1)=−0.005m
- Displacement at x=0.2m is y(0.2)=+0.005m
The general equation for a transverse harmonic wave traveling in the positive x-direction is given by:
y(x,t)=Asin(ωt−kx)
Where:
- A is the amplitude
- ω is the angular frequency
- k is the wave number
The angular frequency ω can be calculated using the formula:
ω=2πf
Substituting the frequency:
ω=2π×500=1000πrad/s
1. For x=0.1m:
−0.005=0.01sin(1000πt−k⋅0.1)
Simplifying gives:
−0.5=sin(1000πt−0.1k)(Equation 1)
0.005=0.01sin(1000πt−k⋅0.2)
Simplifying gives:
0.5=sin(1000πt−0.2k)(Equation 2)
From Equation 1:
1000πt−0.1k=7π6(since sin7π6=−12)
From Equation 2:
1000πt−0.2k=π6(since sinπ6=12)
Subtract Equation 2 from Equation 1:
(1000πt−0.1k)−(1000πt−0.2k)=7π6−π6
This simplifies to:
0.1k=6π6=π
Thus:
k=π0.1=10πrad/m
The wave number k is related to the wavelength λ by:
k=2πλ
So:
λ=2πk=2π10π=0.2m
The wave velocity v can be calculated using:
v=fλ
Substituting the values:
v=500×0.2=100m/s
Substituting A, ω, and k into the wave equation:
y(x,t)=0.01sin(1000πt−10πx)
- Wavelength λ=0.2m
- Wave velocity v=100m/s
- Wave equation:
y(x,t)=0.01sin(1000πt−10πx)
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.2
23 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
When a sound wave of frequency 300 Hz passes through a medium the maximum displacement of a particle of the medium is 0.1 cm . The maximum velocity of the particle is equal to
View SolutionA travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
View SolutionA wave pulse of frequency 200 Hz, on a string moves a distance 8 m in 0.05 s. Calculate the wavelength of wave on string.
View SolutionA sound wave of frequency 500 Hz is producing longitudinal waves in air. The distance between two consecutive rarefactions in the wave is 0.64 m and the amplitude of the oscillation of air particle is 0.002 m. Obtain the displacement equation of this wave.
View SolutionA tuning fork of frequency 100 Hz emits a wave of wavelength 4m. What is the temperature of the atmosphere, if the velocity of sound at 27∘C is 330m/s?
View SolutionFigure shows the shape of part of a long string in which transverse waves are produced by attaching one end of the string to tuning fork of frequency 250 Hz. What is the velocity of the waves?

View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
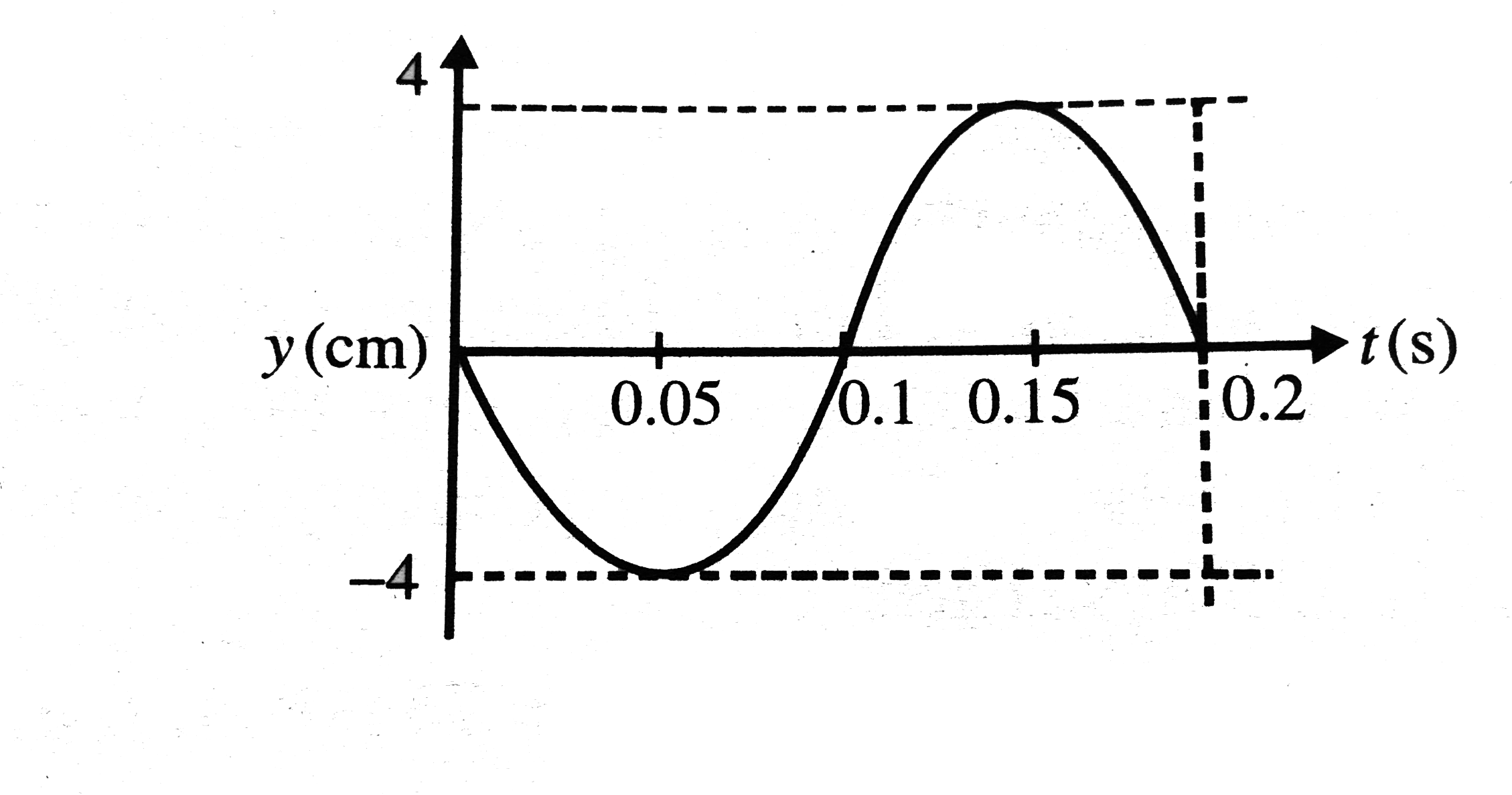
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
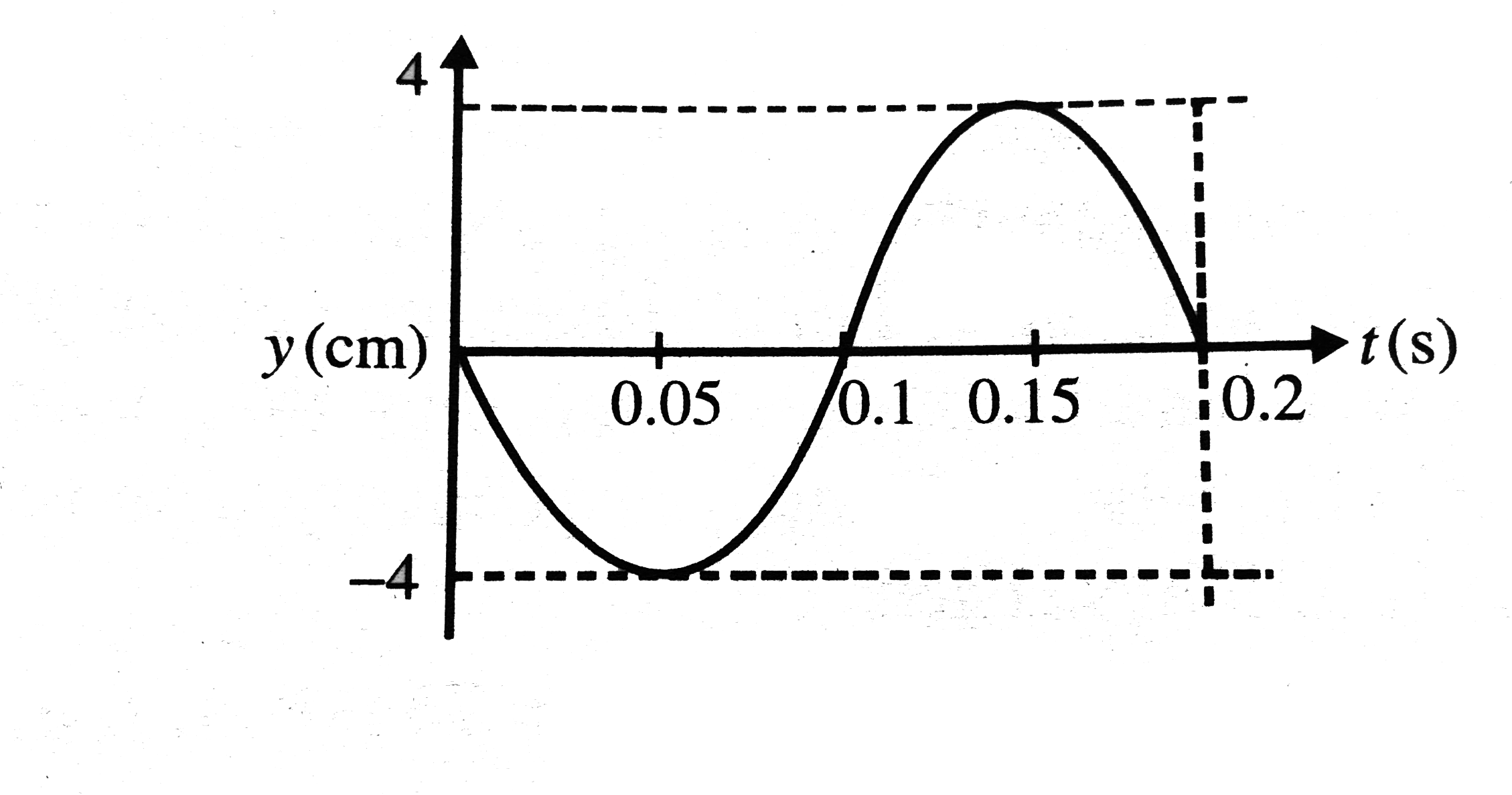
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
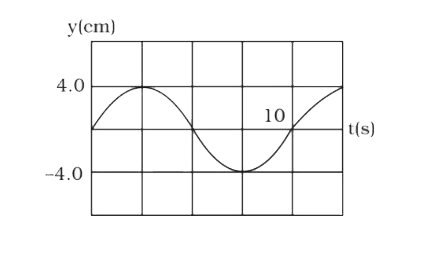
Q. The velocity of propagation of the wave is ?
View SolutionThe frequency of sound is 100 Hz and wavelength is 3m. Calculate the velocity of the wave.
View Solution
