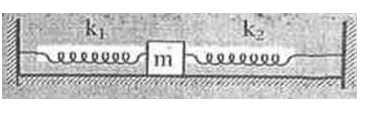
A trolley of mass M is connected to two springs of force constant K1 and K2 as shown in the figure When the trolley is displacement from its equilibrium postion by a distance a and released , it executes S.H.M of frequency f. If it comes to rest after somtimes due to friction, the total energy dissipated as heat is (Dampling forces are weak)

π2ma2f2
2π2ma2f2
2a2(K1+K2)
12a2(K1+K2)
The correct Answer is:B, D
The damping forces are weak. So, all formula of S.H.M. apply.
Amplitude = a
Time period
T=2π√mK1+k2
∴ Frequency, f = 12π
⎷(k1+K_(2)m)
The trolley finally comes to rest, So, the entire energy of oscillation is dissipated as heat due to friction and is given by
E=12ma2ω2=12ma2(2πf)2
=2π2ma2f2
Which is choice (b)
E=12ma2×4π2×14π2(K1+K2m)
E=(a2K1+K22)
Which is choice (d)
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question) based on a given passage/comprehension
9 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Matching Type Questions)
2 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (JEE (Advanced) For IIT Entrance)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A trolley of mass 3.0 kg is connected to two identical rubber bands each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from an equilibrium position by 5.0 cm and released, what is the period of ensuing oscillations?

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
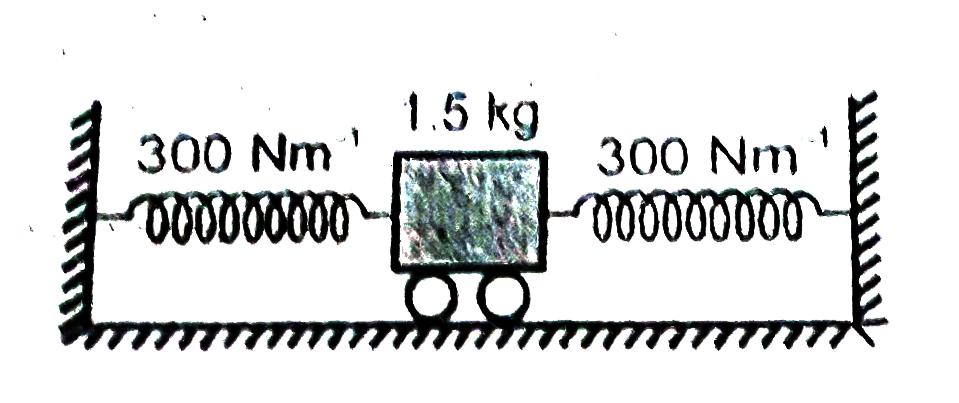
View Solution
Knowledge Check
A mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is
 AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mgTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
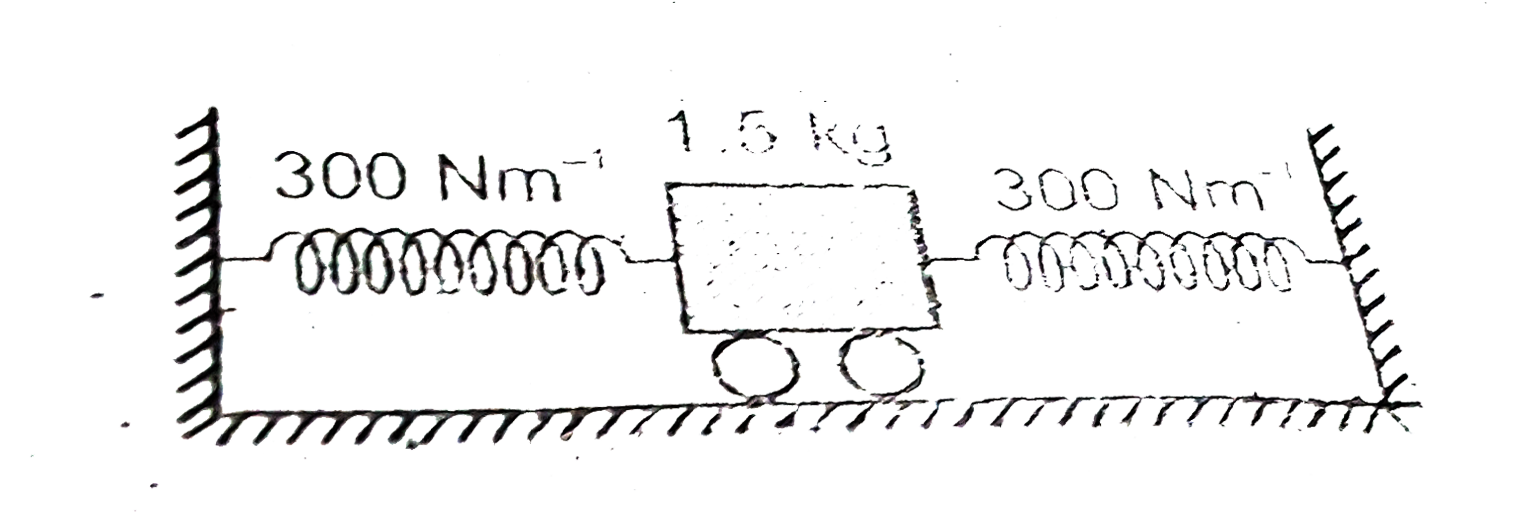
View SolutionA tolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-
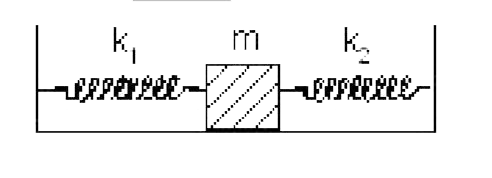
View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
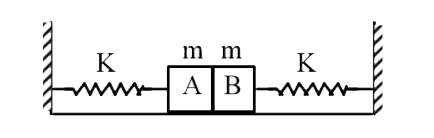
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View Solution
