A trolley, while going down an inclined plane, has an acceleration of 2cm/s2 starting from rest. What will be its velocity 3s after the start ?
To solve the problem, we will use the first equation of motion, which relates initial velocity, acceleration, and time to find the final velocity.
1. Identify the given values:
- Initial velocity (u) = 0 cm/s (since the trolley starts from rest)
- Acceleration (a) = 2 cm/s²
- Time (t) = 3 s
2. Use the first equation of motion:
The first equation of motion is given by:
v=u+at
where:
- v is the final velocity,
- u is the initial velocity,
- a is the acceleration,
- t is the time.
3. Substitute the values into the equation:
v=0+(2cm/s2×3s)
4. Calculate the final velocity:
v=0+6cm/s=6cm/s
5. Conclusion:
The velocity of the trolley 3 seconds after it starts moving down the inclined plane is 6 cm/s.
- Initial velocity (u) = 0 cm/s (since the trolley starts from rest)
- Acceleration (a) = 2 cm/s²
- Time (t) = 3 s
The first equation of motion is given by:
v=u+at
where:
- v is the final velocity,
- u is the initial velocity,
- a is the acceleration,
- t is the time.
v=0+(2cm/s2×3s)
v=0+6cm/s=6cm/s
The velocity of the trolley 3 seconds after it starts moving down the inclined plane is 6 cm/s.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MOTIONEXERCISE - NCERT Exercises10videos
MOTION
- BOOK - PRADEEPCHAPTER - MOTIONEXERCISE - NCERT short answer question7videos
MOTION
- BOOK - PRADEEPCHAPTER - MOTIONEXERCISE - Mock test24videos
MOTION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Model Test paper (1)36videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - SOUNDEXERCISE - Model Test (sec - B)12videos
SOUND
Similar Questions
A solid sphere of mass 0.1kg and radius 2cm rolls down an inclined plane 1.4m in length (slope 1 in 10). Starting from rest, what will be its final velocity?
View SolutionA gridstone has a constant acceleration of 4rads−1. Starting from rest, calculate the angular speed of the grindstone 2.5 s later.
View Solution
Knowledge Check
- Question 1 - Select One
A racing car has a uniform acceleration of 4m/s2. What distance will it cover in 10s after start ?
A200 mB500 mC900 mD400 m - Question 2 - Select One
If a particle rotates along a circle of radius 3 m with an angular acceleration of π2rad/s2 starting from rest, then its average velocity over the time it covers quarter circle is :
A1m/sB2m/sC3m/sD4m/s - Question 3 - Select One
A body has an initial velocity of 3ms−1 and has an acceleration of 1ms−2 normal to the direction of the initial velocity. Then its velocity 4s after the start is.
A7ms−1 along the direction of initial velocity.B7ms−1 along the normal to the direction of initial velocity.C7ms−1 midway between the two directions.D5ms−1 at an angle tan−1(4/3) with the direction of initial velocity.
A gridstone has a constant acceleration of 4 rad s−1. Starting from rest, calculate the angular speed of the grindstone 2.5 s later.
View SolutionAn object starting from rest travels 20m in first 2s and 160m in next 4s. What will be the velocity after 7s from the start.
View SolutionA body has an initial velocity of 3m/s and has an acceleration of 1m/sec2 normal to the direction of the initial velocity. Then its velocity 4 seconds after the start is
View SolutionThe displacement of a body in 8 s starting from rest with an acceleration of 20cms−2 is
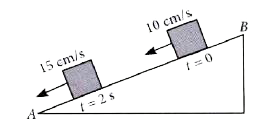
View SolutionAn object is sliding down an inclined plane. The velocity changes at a constant rate from 10 cm/s to 15 cm/s in two seconds. What is its acceleration ?
 View Solution
View Solution
