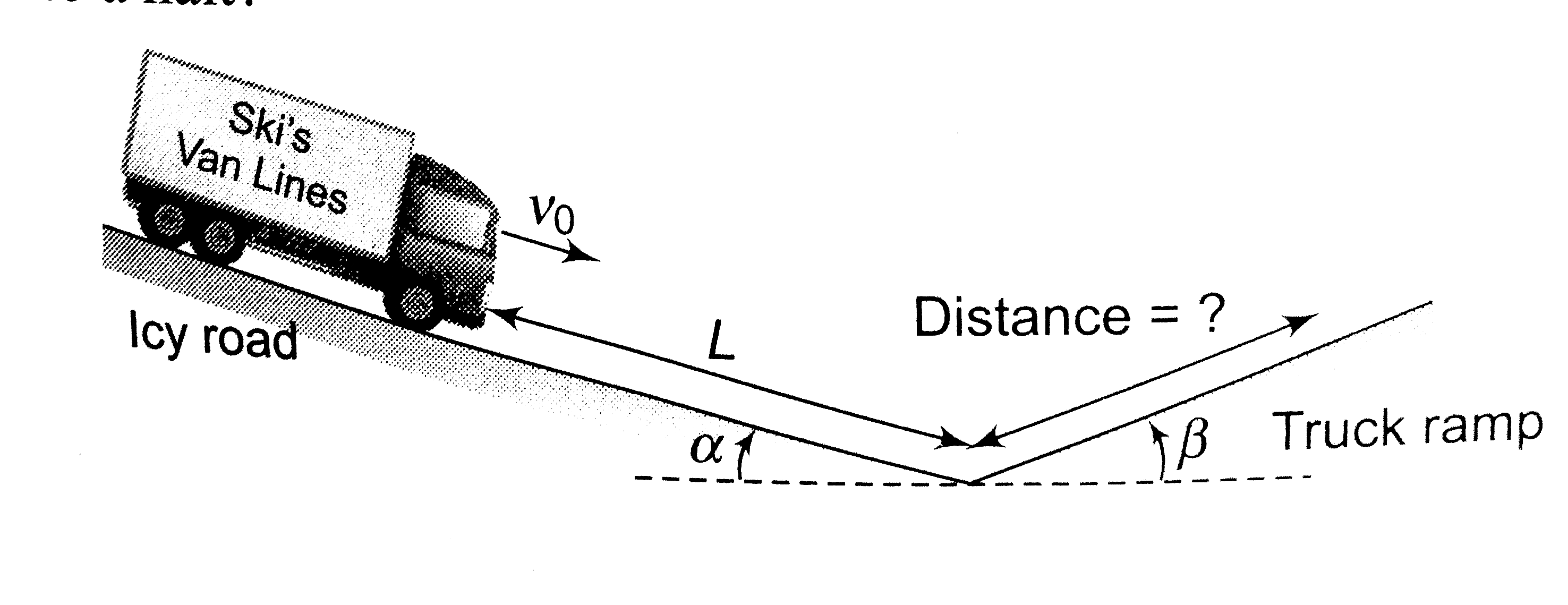
A truck with mass has a brake failure while going down an icy mountain road of constant downwards slope angle (see figure) . Initial , the truck is moving downhill at speed . After carrying downhill a distance with negligible friction for the truck driver steers the runaway vehicle onto a runway truck rump of constant upward slope angle . The truck rump has to soft sand surface for which the coefficient of rolling friction is . What is the distance that the truck moves up the rump before coming to a halt?
A
B
C
D
None of these
Video Solution
Text Solution
The correct Answer is:A
Denote the distance the truck moves up the ramp by
sin betaW_(other =- mu_(r) mgx cos betax=(K_(1)+mgL sin beta)/(mg (sin beta +mu_(r) cos beta))=((v_(0)^(2)//2g)+L sin beta)/(sin beta + mu_(r) cos beta).
|
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Circular Motion In Vertical Plane
21 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Potential Energy, Conservative And Non-Conservative Forces
28 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
A truck with mass m has a brake failure while going down an icy mountain road of constant downwards slope angle α (see figure) . Initial , the truck is moving downhill at speed v0 . After carrying downhill a distance L with negligible friction for the truck driver steers the runaway vehicle onto a runway truck rump of constant upward slope angle Bη . The truck rump has to soft sand surface for which the coefficient of rolling friction is μr. What is the distance that the truck moves up the rump before coming to a halt?
 A(v20/2g)+Lsinαsinβ+μr,cosβB(v20g)−Lsinα(sinβ+μr,cosβ)C(v20/2g)+Lsinαsinβ−μr,cosβDNone of these
A(v20/2g)+Lsinαsinβ+μr,cosβB(v20g)−Lsinα(sinβ+μr,cosβ)C(v20/2g)+Lsinαsinβ−μr,cosβDNone of theseA truck with mass m has a brake failure while going down an icy mountain road of constant down and slope angle a (see figure). Initially, the truck is moving downhill at speed V. After careening downhill a distance L with negligible friction, the truck driver steers the runaway vehicle onto a runway truck ramp of constant upward slope angle β . The truck ramp has to soft sand surface for which the coefficient of rolling friction is μr What is the distance that the truck moves up the ramp before coming to a halt?
 A(ν20/2g)+Lsinαsinβ−μrcosβB(ν20/g)−Lsinαsinβ+μrcosβC(ν20/2g)+Lsinαsinβ−μrcosβDNone of these
A(ν20/2g)+Lsinαsinβ−μrcosβB(ν20/g)−Lsinαsinβ+μrcosβC(ν20/2g)+Lsinαsinβ−μrcosβDNone of theseA truck covers a distance of 1200 km in 40 hours. What is the average speed of the truck?
A30 km/hrB40 km/hrC60 km/hrD45 km/hr
Why a truck or a motor but has much wider tyres?
View SolutionA truck covers a distance of 1800 km in 40 hours. What is the average speed of the truck?
View SolutionDrums of oil are carried in a truck. If a constant accleration is applied on the turck, the surface of the drum will-
View SolutionThe speed of a truck is 13 rd the speed of a train . The train covers 1230 km is 5 hours . What is the speed of the truck ?
View Solutiontruck is moving with a speed of 15 m/s. A car chasing this truck with a speed of 10 m/s fires a bullet at truck with muzzle velocity 90 km/h. The speed with which the bullet hit the truck is
View Solution
