A tunnel ois dug along a chord of the earth a perpendicular distance from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
The correct Answer is:B
To find the force exerted by the wall of the tunnel on a particle of mass m when it is at a distance x from the center of the tunnel, we can follow these steps:
Step 1: Understand the Setup
We have a tunnel dug along a chord of the Earth, at a perpendicular distance of R/2 from the center of the Earth. We need to find the gravitational force acting on a mass m located at a distance x from the center of the tunnel.
Step 2: Define the Geometry
Let R be the radius of the Earth. The distance from the center of the Earth to the tunnel is R/2. The distance from the center of the tunnel to the mass m is d, which can be expressed in terms of x and R/2 using the Pythagorean theorem:
d=√(R/2)2+x2
Step 3: Calculate the Mass of the Sphere
The mass M′ of the sphere of radius d (the sphere that would enclose the mass m) is given by:
M′=43πd3ρ
where ρ is the density of the Earth. The total mass M of the Earth is:
M=43πR3ρ
Step 4: Relate the Masses
Using the ratio of the masses, we can express M′ in terms of M:
M′M=d3R3
Thus,
M′=M⋅d3R3
Step 5: Calculate the Gravitational Force
The gravitational force F acting on the mass m due to the mass M′ is given by Newton's law of gravitation:
F=GmM′d2
Substituting M′:
F=Gm(M⋅d3R3)d2=GmMdR3
Step 6: Determine the Direction of the Force
The force F acts towards the center of the Earth. Since we are interested in the component of force acting along the direction of the tunnel, we need to find the angle θ formed with the vertical. Using trigonometry:
cosθ=R/2d
Step 7: Substitute cosθ into the Force Equation
The effective force acting along the tunnel is:
Ftunnel=Fcosθ=GmMdR3⋅R/2d=GmMR2R3=GmM2R2
Final Result
Thus, the force exerted by the wall of the tunnel on the particle of mass m when it is at a distance x from the center of the tunnel is:
F=GmM2R2
We have a tunnel dug along a chord of the Earth, at a perpendicular distance of R/2 from the center of the Earth. We need to find the gravitational force acting on a mass m located at a distance x from the center of the tunnel.
Let R be the radius of the Earth. The distance from the center of the Earth to the tunnel is R/2. The distance from the center of the tunnel to the mass m is d, which can be expressed in terms of x and R/2 using the Pythagorean theorem:
d=√(R/2)2+x2
The mass M′ of the sphere of radius d (the sphere that would enclose the mass m) is given by:
M′=43πd3ρ
where ρ is the density of the Earth. The total mass M of the Earth is:
M=43πR3ρ
Using the ratio of the masses, we can express M′ in terms of M:
M′M=d3R3
Thus,
M′=M⋅d3R3
The gravitational force F acting on the mass m due to the mass M′ is given by Newton's law of gravitation:
F=GmM′d2
Substituting M′:
F=Gm(M⋅d3R3)d2=GmMdR3
The force F acts towards the center of the Earth. Since we are interested in the component of force acting along the direction of the tunnel, we need to find the angle θ formed with the vertical. Using trigonometry:
cosθ=R/2d
The effective force acting along the tunnel is:
Ftunnel=Fcosθ=GmMdR3⋅R/2d=GmMR2R3=GmM2R2
Thus, the force exerted by the wall of the tunnel on the particle of mass m when it is at a distance x from the center of the tunnel is:
F=GmM2R2
Topper's Solved these Questions
Similar Questions
(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre.
(b) A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View Solution
Knowledge Check
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
A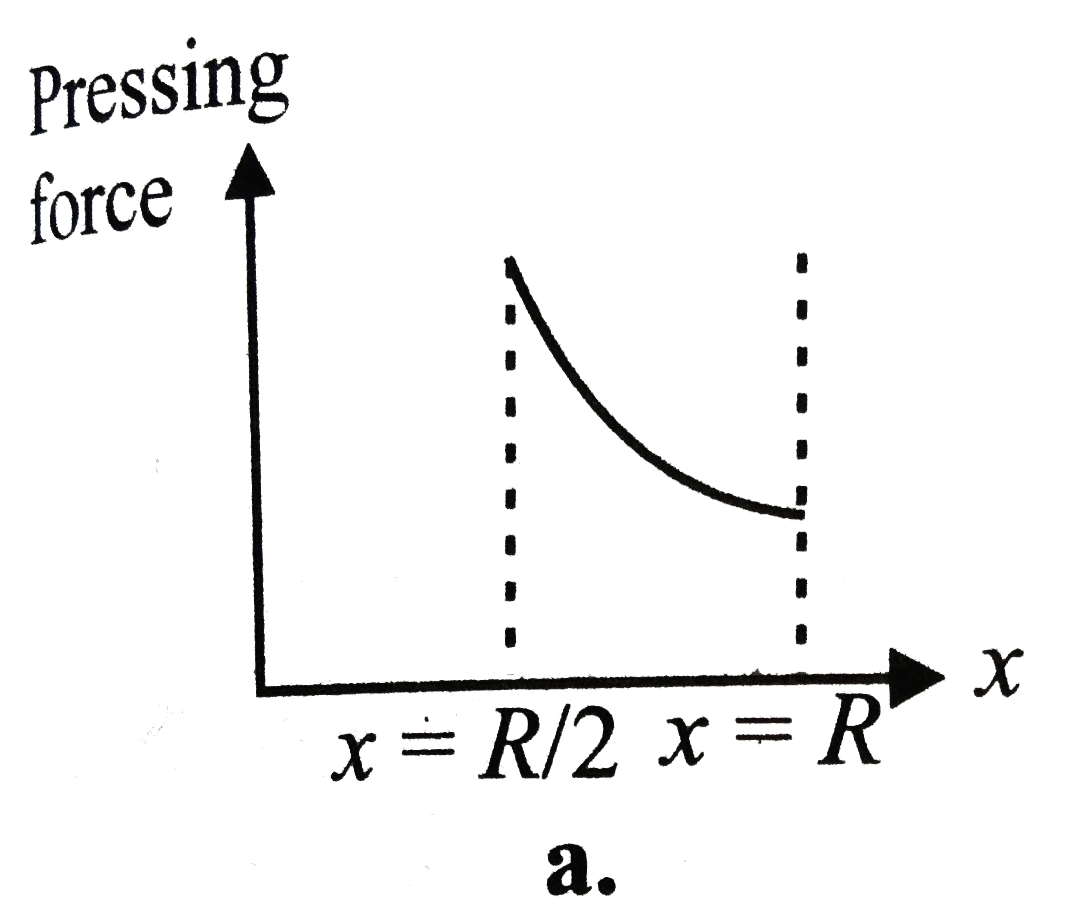 B
B C
C D
D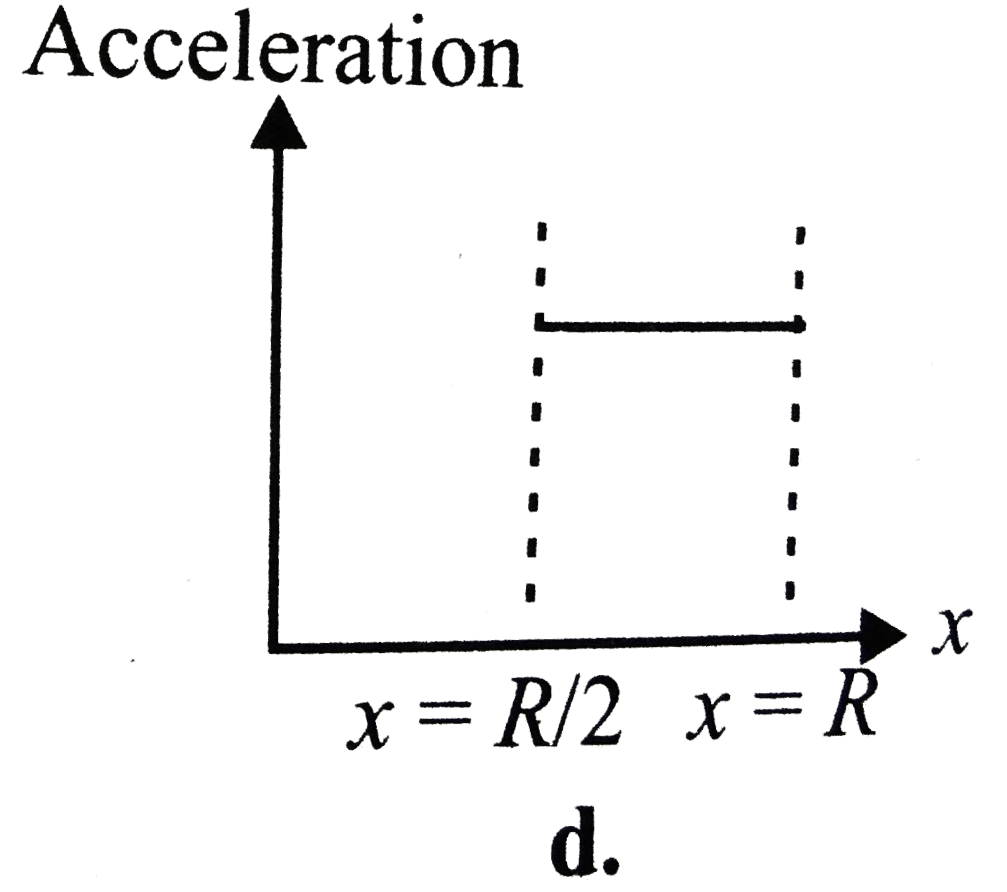
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√RgA body of mass m is moved from the centre of the earth to a infinite distance from its centre. The value of g will
Anot change in magnitude and directionBincrease from zero to infinityCincrease from zero to g and then decrease from g to zeroDdecrease from infinity to zero
Assume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionAssume that a tunnel is dug along a cord of earth at a perpendicular distance R2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
View SolutionA tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA tunnel is dug along a chord of non rotating earth at a distance d=R2 [R = radius of the earth] from its centre. A small block is released in the tunnel from the surface of the arth. The block comes to rest at the centre (C) of the tunnel. Assume that the friction coefficient between the block and the tunnel wall remains constant at μ.
 Calculate work done by the friction on the block. Calculate μ.
Calculate work done by the friction on the block. Calculate μ.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View Solution
