A turning fork vibrating at 500Hz falls from rest accelerates at 10m/s2.
How far below the point of release is the tuning fork when wave with a frequency of 475Hz reach the release point ?
16.9m
16m
1.69m
1.6m
The correct Answer is:A
To solve the problem, we need to determine how far below the point of release the tuning fork is when the wave with a frequency of 475 Hz reaches the release point. We will follow these steps:
Step 1: Understand the given information
- The tuning fork vibrates at a frequency of fs=500Hz.
- It falls from rest with an acceleration of g=10m/s2.
- The frequency of the wave reaching the release point is f′=475Hz.
- The speed of sound in air is v=340m/s.
Step 2: Use the Doppler effect to find the speed of the tuning fork
The apparent frequency f′ can be related to the source frequency fs using the Doppler effect formula:
f′=fsv+v0v−vs
Where:
- v0=0 (the observer is stationary),
- vs is the speed of the source (the tuning fork).
Substituting the known values:
475=500340+0340−vs
Step 3: Rearranging the equation to solve for vs
Cross-multiplying gives:
475(340−vs)=500×340
Expanding and rearranging:
475×340−475vs=500×340
−475vs=500×340−475×340
−475vs=(500−475)×340
−475vs=25×340
vs=−25×340475
Calculating vs:
vs≈−17.9m/s
Step 4: Calculate the time taken for the sound wave to reach the release point
The time taken t′ for the sound wave to travel back to the release point can be calculated as:
t′=dv
Where d is the distance the tuning fork has fallen when the wave reaches the release point.
Step 5: Determine the distance fallen by the tuning fork
Using the formula for distance under constant acceleration:
d=ut+12at2
Since the initial velocity u=0:
d=12gt′2
Substituting g=10m/s2 and t′:
d=12×10×(t′)2
Step 6: Calculate the time t′
Since the tuning fork is falling, we can express d in terms of vs:
t′=dvs
Substituting vs≈17.9m/s:
d=12×10×(d17.9)2
Step 7: Solve for d
Rearranging gives:
d=517.92d2
This is a quadratic equation in d. Solving this will give the distance.
Final Calculation
After solving, we find:
d≈16.875m
Rounding to one decimal place gives:
d≈16.9m
Conclusion
The tuning fork is approximately 16.9 meters below the point of release when the wave with a frequency of 475 Hz reaches the release point.
---
- The tuning fork vibrates at a frequency of fs=500Hz.
- It falls from rest with an acceleration of g=10m/s2.
- The frequency of the wave reaching the release point is f′=475Hz.
- The speed of sound in air is v=340m/s.
The apparent frequency f′ can be related to the source frequency fs using the Doppler effect formula:
f′=fsv+v0v−vs
Where:
- v0=0 (the observer is stationary),
- vs is the speed of the source (the tuning fork).
475=500340+0340−vs
Cross-multiplying gives:
475(340−vs)=500×340
Expanding and rearranging:
475×340−475vs=500×340
−475vs=500×340−475×340
−475vs=(500−475)×340
−475vs=25×340
vs=−25×340475
Calculating vs:
vs≈−17.9m/s
The time taken t′ for the sound wave to travel back to the release point can be calculated as:
t′=dv
Where d is the distance the tuning fork has fallen when the wave reaches the release point.
Using the formula for distance under constant acceleration:
d=ut+12at2
Since the initial velocity u=0:
d=12gt′2
Substituting g=10m/s2 and t′:
d=12×10×(t′)2
Since the tuning fork is falling, we can express d in terms of vs:
t′=dvs
Substituting vs≈17.9m/s:
d=12×10×(d17.9)2
Rearranging gives:
d=517.92d2
This is a quadratic equation in d. Solving this will give the distance.
After solving, we find:
d≈16.875m
Rounding to one decimal place gives:
d≈16.9m
The tuning fork is approximately 16.9 meters below the point of release when the wave with a frequency of 475 Hz reaches the release point.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer
9 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct Answer Type
56 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
A turning fork vibrating at 500Hz falls from rest accelerates at 10m/s2.
Velocity of the tuning fork when waves with a frequency of 475Hz reach the release point is ( Take the speed of sound in air to be 340m/s).
View SolutionA turning fork vibrating at 500Hz falls from rest accelerates at 10m/s2.
Time taken by the waves with a frequency of 475Hz to reach the release point is nearly
View SolutionA piano note is compared to a tuning fork vibrating at 440 Hz. Three beats per second are listened by the piano tuner. When the tension in the string is increased slightly, the beat frequency increases. What was the initial frequency of the piano wire ?
View SolutionA student holds a tuning fork ocillating at 2456 Hz. He walks towards a wall at a constant speed of 1.33ms. (a) What beat frequency does the student observes between the tuning fork and its echo? (b) How fast must he walk away from the wall to observe a beat frequency of 5.00Hz?
View SolutionA tuning fork is vibrating at frequency 100Hz. When another tuning fork is sounded simutaneously.=, 4 beats per second are heard. When some mass is added to the tuning fork of 100Hz, beat frequency decreases. Find the frequency of the other tuning fork.
View Solution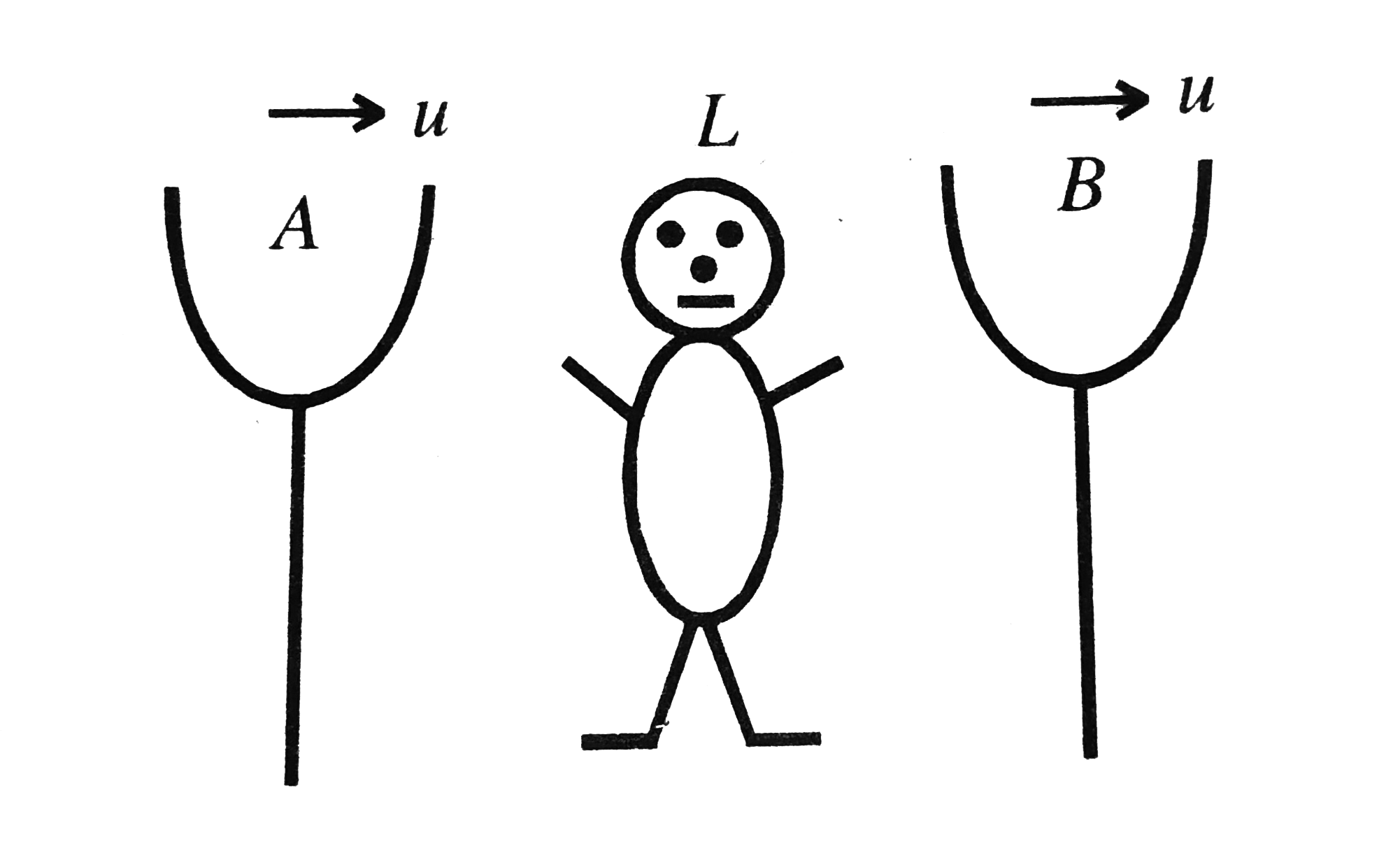 Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
View Solution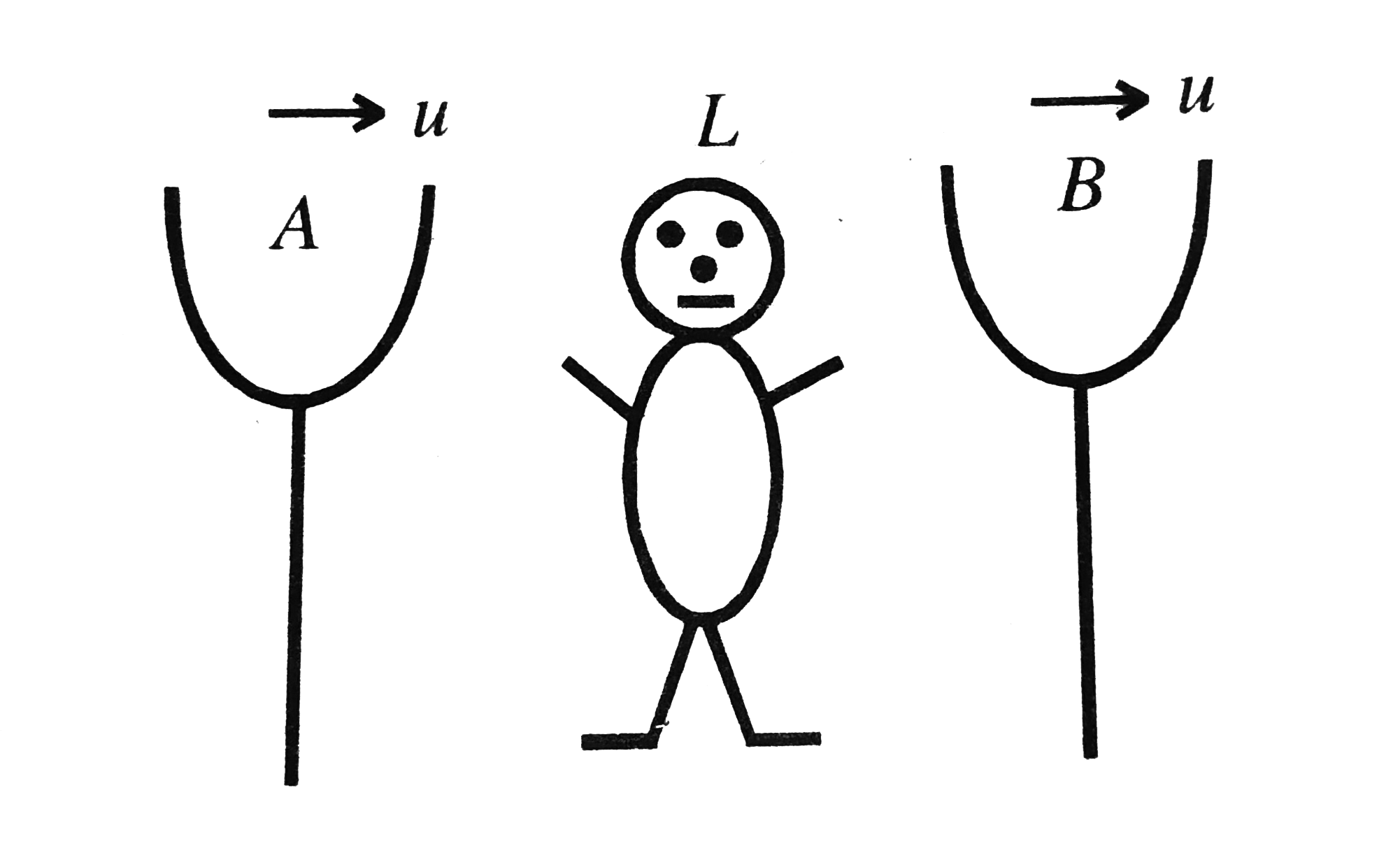 Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
View SolutionAn organ pipe is sounded with a tuning fork of frequency 256 Hz. When the air in the pipe is at a temperature of 15∘C, 23 beats are heard in 10 sec. When the tuning fork is loaded with a small piece of wax, the beat frequency is found to decrease. What change of temperature of the air in the pipe is necessary to bring the pipe and the unloaded fork into unison?
View SolutionWhen a tuning fork vibrates with 1.0m or 1.05m long wire of a , 5 beats per second are produced in each case. If the frequency of the tuning fork is 5f (in Hz) find f.
View SolutionA sonometer wire having a length of 1.50 m between the bridges vibrates in its second harmonic in resonance with a tuning fork of frequency 256 Hz. What is the speed of the transverse wave on the wire ?
View Solution
