A U-tube is partially filled with water. Oil which does not mix with water is next poured into one side, until water rises by 25 cm on the other side. If the density of oil 0.8g/cm3. The oil level will stand higher than the water by
6.25cm
12.50cm
31.75cm
25cm
The correct Answer is:B
To solve the problem, we need to analyze the U-tube filled with water and oil. We will use the principle of hydrostatic pressure, which states that the pressure at a given depth in a fluid is the same regardless of the fluid type, as long as the points are at the same horizontal level.
1. Understand the Setup:
- We have a U-tube partially filled with water.
- Oil is poured into one side of the U-tube, causing the water level to rise by 25 cm on the other side.
2. Define Variables:
- Let the density of water be ρw=1g/cm3 (or 1000kg/m3).
- Let the density of oil be ρo=0.8g/cm3 (or 800kg/m3).
- Let the height of the oil column be h.
3. Apply Hydrostatic Pressure Principle:
- At the level where the oil and water meet, the pressure exerted by the oil column must equal the pressure exerted by the water column on the other side.
- The pressure due to the oil column is given by:
Poil=ρo⋅g⋅h
- The pressure due to the water column (after rising by 25 cm) is:
Pwater=ρw⋅g⋅(25cm)
4. Set the Pressures Equal:
- Since the pressures must balance at the same horizontal level, we have:
ρo⋅g⋅h=ρw⋅g⋅25
- Note that g cancels out from both sides:
ρo⋅h=ρw⋅25
5. Substitute the Known Densities:
- Substitute the values of ρo and ρw:
0.8⋅h=1⋅25
6. Solve for h:
- Rearranging gives:
h=250.8=31.25cm
7. Find the Height Difference:
- Since the oil level stands higher than the water, we need to find the difference in height:
Height difference=h−25cm=31.25cm−25cm=6.25cm
Final Answer:
The oil level will stand higher than the water by 6.25 cm.
- We have a U-tube partially filled with water.
- Oil is poured into one side of the U-tube, causing the water level to rise by 25 cm on the other side.
- Let the density of water be ρw=1g/cm3 (or 1000kg/m3).
- Let the density of oil be ρo=0.8g/cm3 (or 800kg/m3).
- Let the height of the oil column be h.
- At the level where the oil and water meet, the pressure exerted by the oil column must equal the pressure exerted by the water column on the other side.
- The pressure due to the oil column is given by:
Poil=ρo⋅g⋅h
- The pressure due to the water column (after rising by 25 cm) is:
Pwater=ρw⋅g⋅(25cm)
- Since the pressures must balance at the same horizontal level, we have:
ρo⋅g⋅h=ρw⋅g⋅25
- Note that g cancels out from both sides:
ρo⋅h=ρw⋅25
- Substitute the values of ρo and ρw:
0.8⋅h=1⋅25
- Rearranging gives:
h=250.8=31.25cm
- Since the oil level stands higher than the water, we need to find the difference in height:
Height difference=h−25cm=31.25cm−25cm=6.25cm
The oil level will stand higher than the water by 6.25 cm.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of 10mm above the water level on the other side. Meanwhile the water rises by 65mm from its original level (see diagram). The density of the oil is:
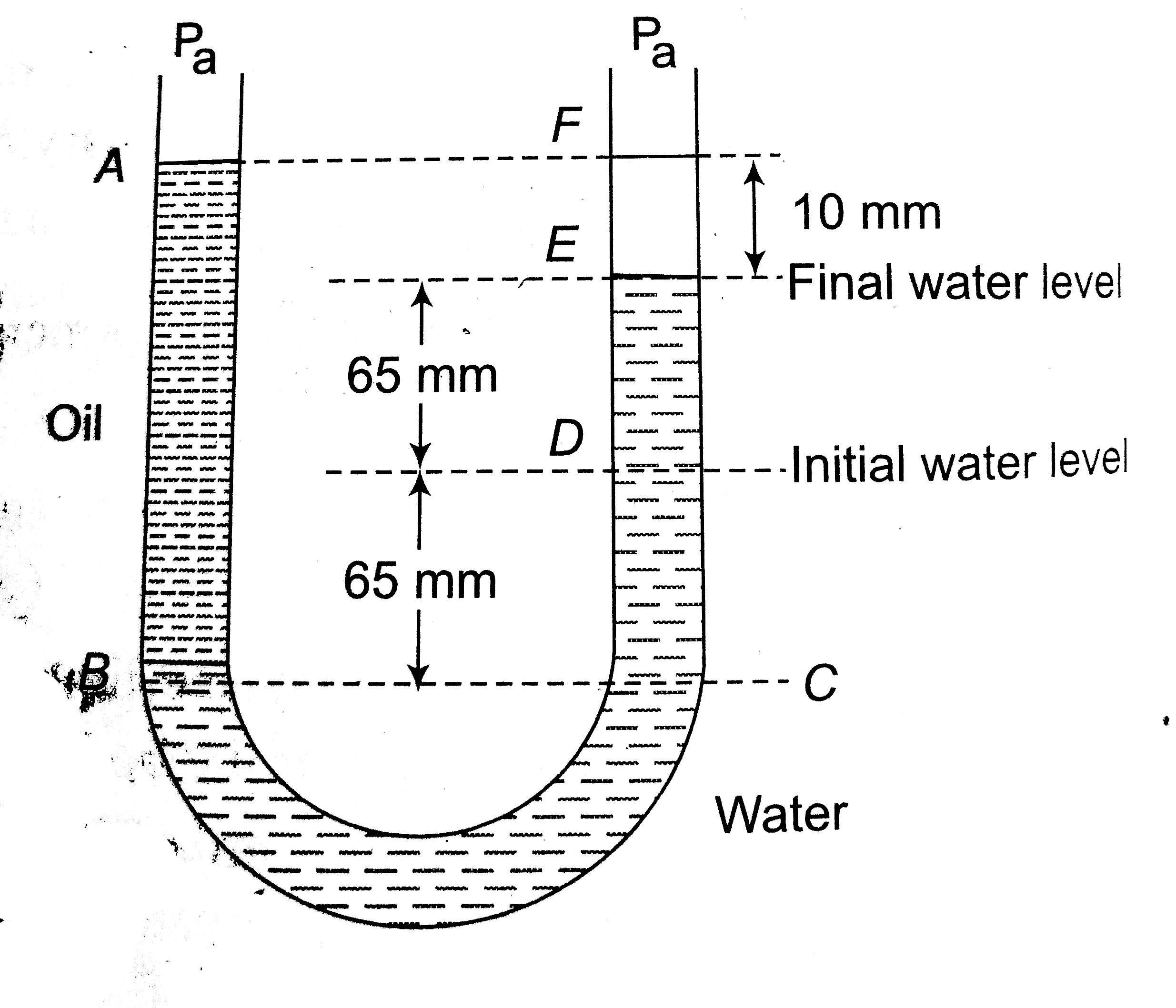
View SolutionA U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of 10mm above the water level on the other side. Meanwhile the water rises by 65mm from its original level (see diagram). The density of the oil is:

View SolutionA U tube is first partially filled with mercury. Then water is added in one arm and an oil is added in the other arm. Find the ratio of water and oil columns so that mercury level is same in both the arms of U tube. Given : Density of water =103kgm−3 , density of oil =900kgm−3.
View SolutionA sphere of radius 5cm is immersed in water filled in a cylinder, the level of water rises 53cm. Find the radius of the cylinder.
View SolutionVolume occupied by one molecule of water (density = 1 g cm−3)
View SolutionA drop of olive oil of radius 0.25 mm spreads into a circular film of radius 5 cm on the water surface. Estimate the molecular size of the olive oil
View SolutionTwo capillary tubes of diameters 3.0mm and 6.0mm are joined together to form a U-tube open at both ends. If the U-tube is filled with water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3×102N/m. Take the angie of contact to be zero and density of water to be 103kg/m3(g=9.8m/s2)
View SolutionA capillary due sealed at the top has an internal radius of r=0.05cm. The tube is placed vertically in water, with its open end dipped in water. Find greatest interger corresponding to the length (in water) of such a tube be for the water in it to rise in these conditions to a height h=1cm ? The pressure The pressure of the air is P0=1atm. =7cm of Hg , density of Hg=13.6/cm3, g=9.8m/sec2 The surface tension of water is σ=70dyne/cm. (assume temperature of air in the tube is constant)
View SolutionIf oil of density higher than water is used in place of water in a resonance tube how does the frequency change?
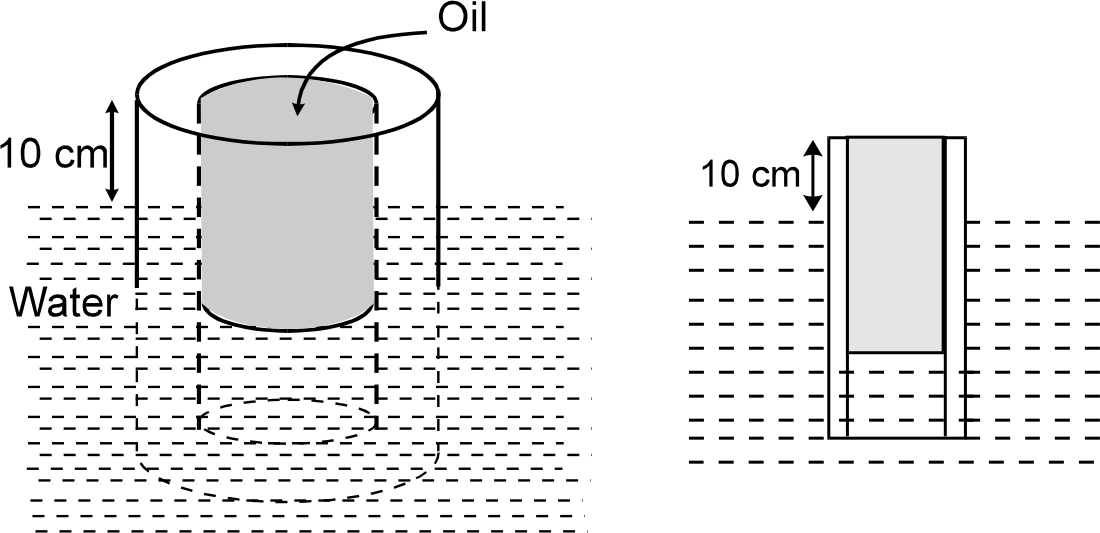
View SolutionA tube with both ends open floats vertically in water. Oil with a density 800 kg/m3 is poured into the tube. The tube is filled with oil upto the top end while in equilibrium. The portion out of the water is of length 10 cm. The length of oil in the tube is 10αcm. Find α (assume effect of surface tension is neglible):
View Solution
