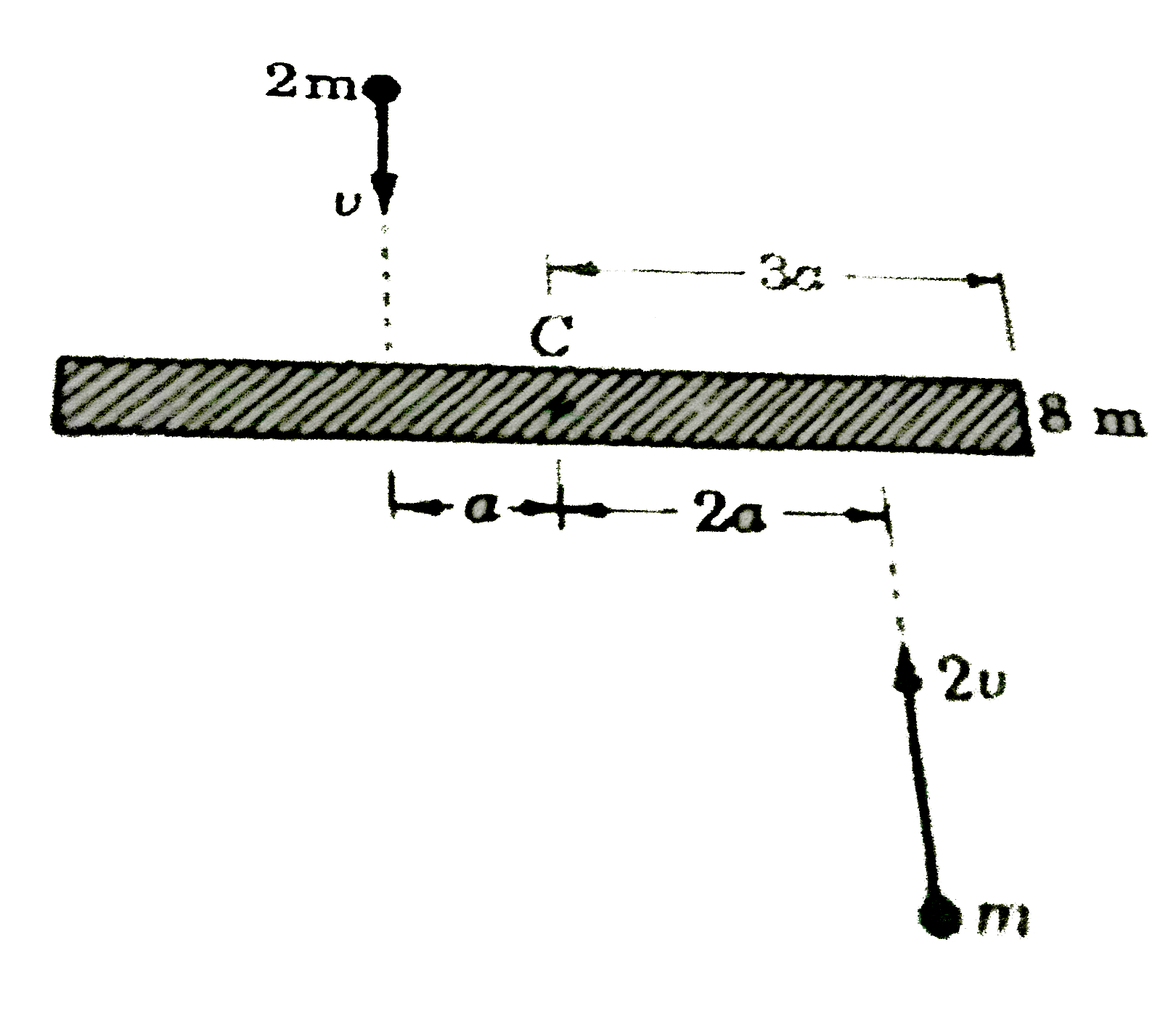
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and vc respecitvely, we have after collison
![A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by omega, E and vc respecitvely, we have after collison](https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_RM_C06_042_Q01.png)
v0=0
ω=(3v/5a)
ω=(v/5a)
E=(3mv2/5)
The correct Answer is:A, C, D
(a) As exteranl force is zero, so linear momentum is conserved.
i.e. −2m×v+m×2v+0=(2m+m+8m)v0
∴V0=0
(c ) As external torques is also zero, so angualr momentum is conserved, i.e.,
m1v1r1+m2v2r2=(I1+I2+I¯)ω
(2m)va+m(2v)(2a)
=[2m(a)2+m(2a)2+8m×(6a)212]ω
6mva=30ma2ω
ω=v5a
(d) E=12Iω2=13(30ma2)(v5a)2
=3mv25[∵I=30ma2]
Similar Questions
A uniform bar of length 6a and mass 8 m lies on a smooth horizontal table. Two point-masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively strike the bar as shown in Fig, and stick to the bar after collision.
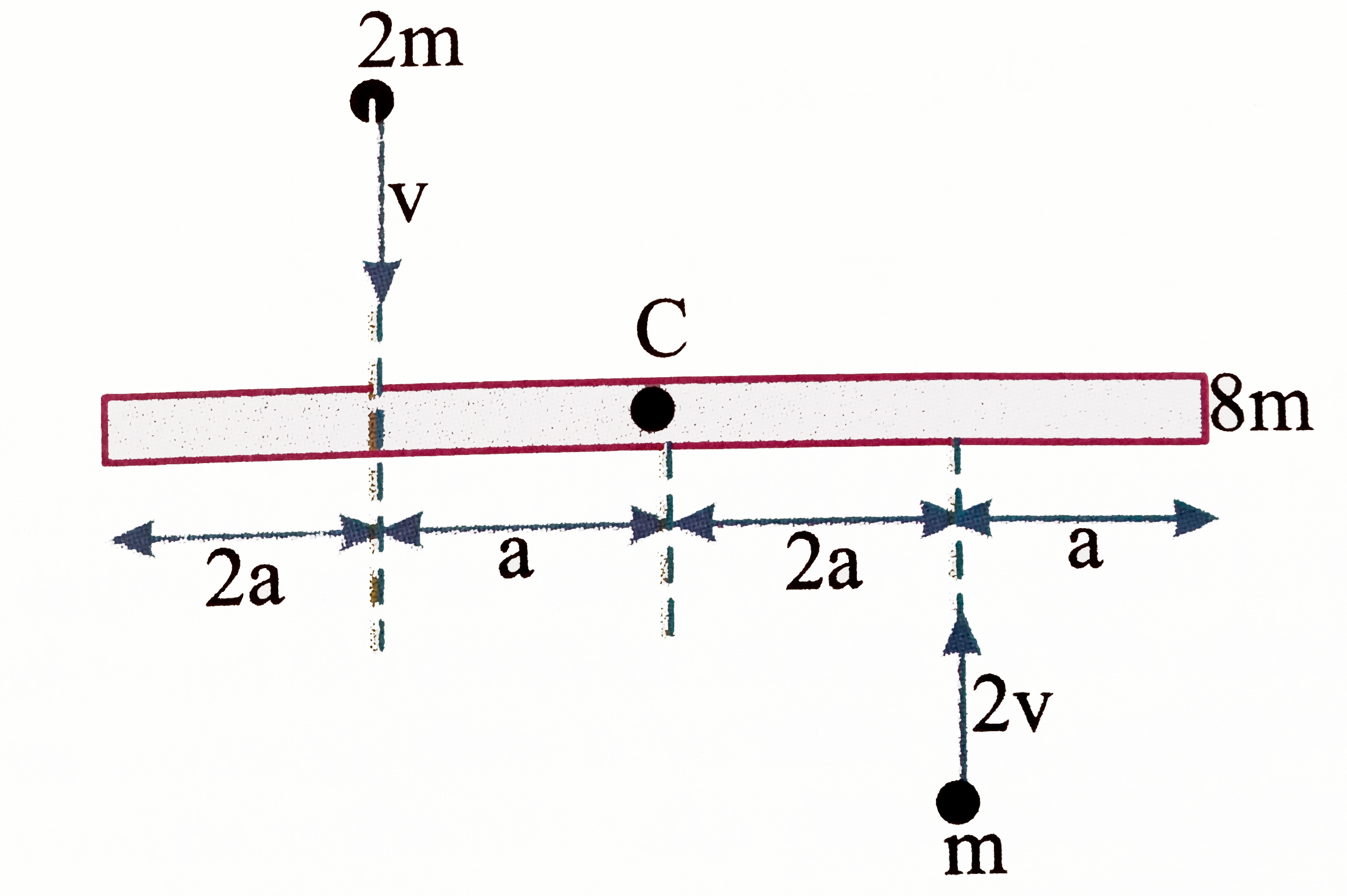
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively, strike the bar (as shown in figure) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c) total kinetic energy, just after collision.
View Solution
Knowledge Check
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v, respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and VC, respectively, we have after collision
 AVc=0Bω=3v5aCω=v5aDE=3mv25
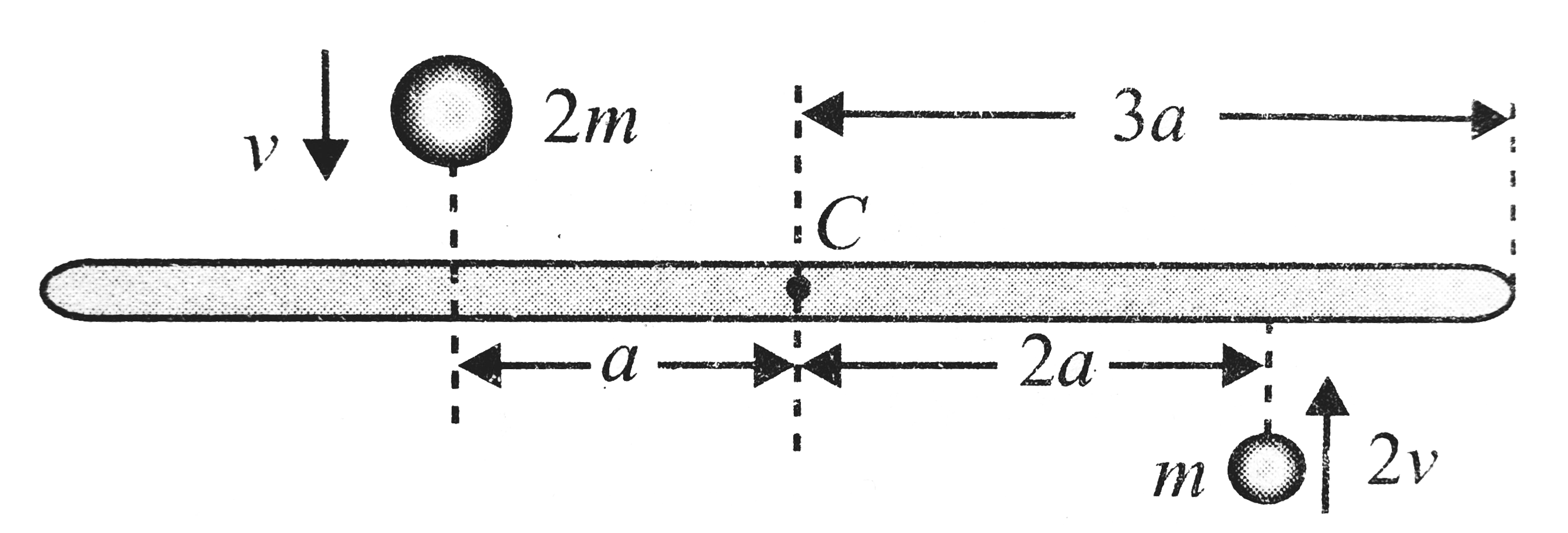
AVc=0Bω=3v5aCω=v5aDE=3mv25A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving with the same horizontal speed 2v and v respectively, strike the bar as shown in the figure and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy, and centre of mass velocity after collision by ω, E and vC respectively, we have after collision
 AvC=0Bω=3v5aCω=v5aDE=3mv25
AvC=0Bω=3v5aCω=v5aDE=3mv25A uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
Aangular velocity of the system after collision is 25vlBangular velocity of the system after collision is v2lCThe loss in kinetic energy of the system as a whole as a result of the collision 310mv2DThe loss in kinetic energy of the system as a whole as a result of the collision 7mv224
A.uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar and stick to the bar. The bar is set in rotation. The rotational energy E=pmv2q then find (p+q).
'(##CEN_KSR_PHY_JEE_C09_E01_038_Q20##)'
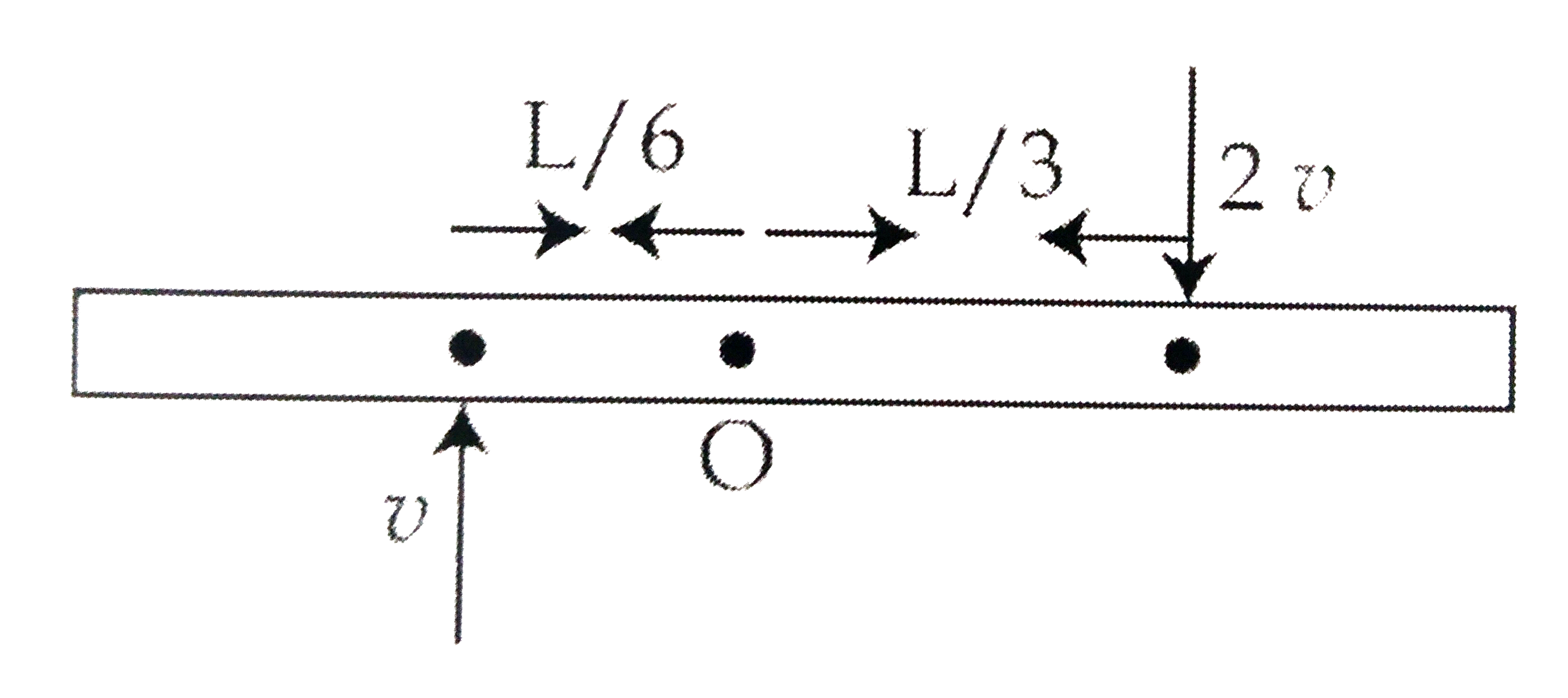
View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances L3andL6 respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be
View SolutionA uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.
View Solution