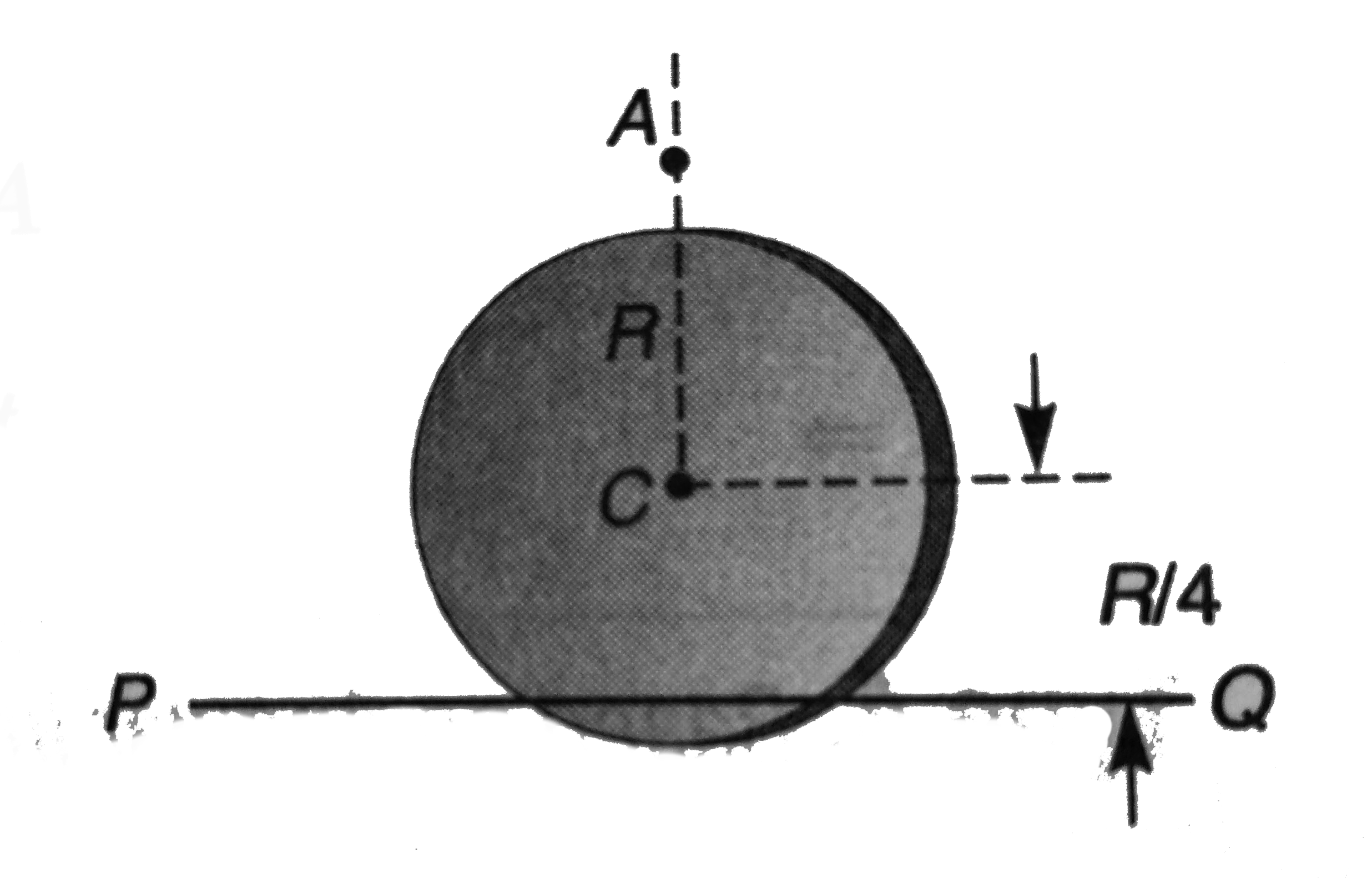
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
During the fall the disc mas system gains rotational kinetic energy. This is the expense of potential energy.

Applying conservation of mechanical energy, we get
Initial total energy = Final total energy
mg(2R+2R4)+mg(R+2R4)=mgR+12Iω2
where I=MI of the disc mass system about PQ
=mg+10R4+mg(6R)4=mgR+12ω2
⇒3mgR=12IΩ2
⇒w=(√6mgR1)...........i
(I)PQ=(Idisc)PQ+(Imass)PQ
=[mR24+M(R4)2]+m(5R4)2
[Therfore MI of disc about the diameter =(14)MR2]
=(mR2[4+1+25])15mR28...........ii
Form eqn i and ii ω=√6mgR×815mR2=√16g5R
Let v be velocity of mass m at the lowest point of rotation
v=ω(R+R4)
=√16g5g×5R4=√5gR
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions

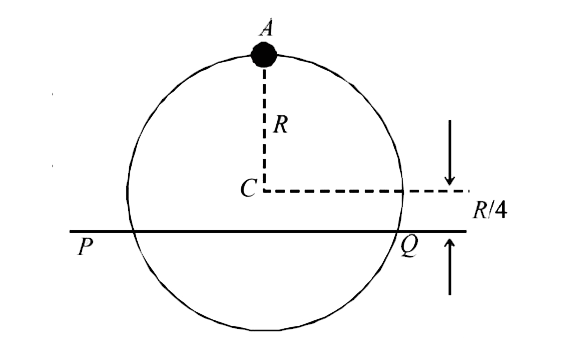
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionA uniform circula disc has radius R and mass m. A particle also of mass m, is fixed at a point A on the edge of the disc as shown in figure. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially, the disc is held vertical with the point A at its highes position.
View Solution
Knowledge Check
The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is
AMR2B12MR2C32MR2D72MR2The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
A12MR2BMR2C72MR2D32MR2A quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
 A12mR2ω2B14mR2ω2C18mR2ω2D116mR2ω2
A12mR2ω2B14mR2ω2C18mR2ω2D116mR2ω2
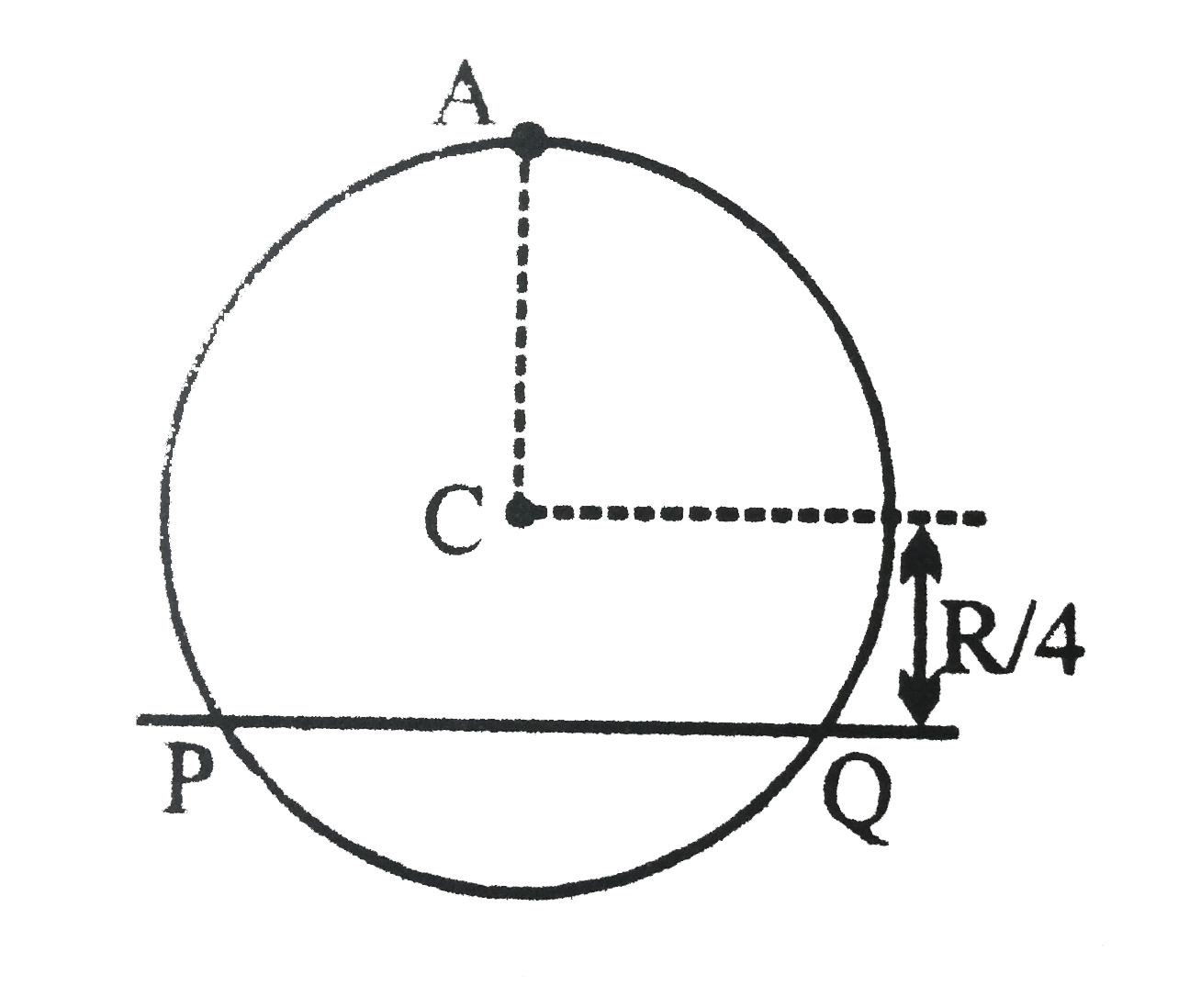
A uniform circular disc has radius R and mass m. A particle also of mass m is fixed at a point A on the wedge of the disc as in fig. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall so that it tarts rotating about PQ. Find the linear speed of the particle at it reaches its lowest position.
 .
.
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at this instant is
View SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information
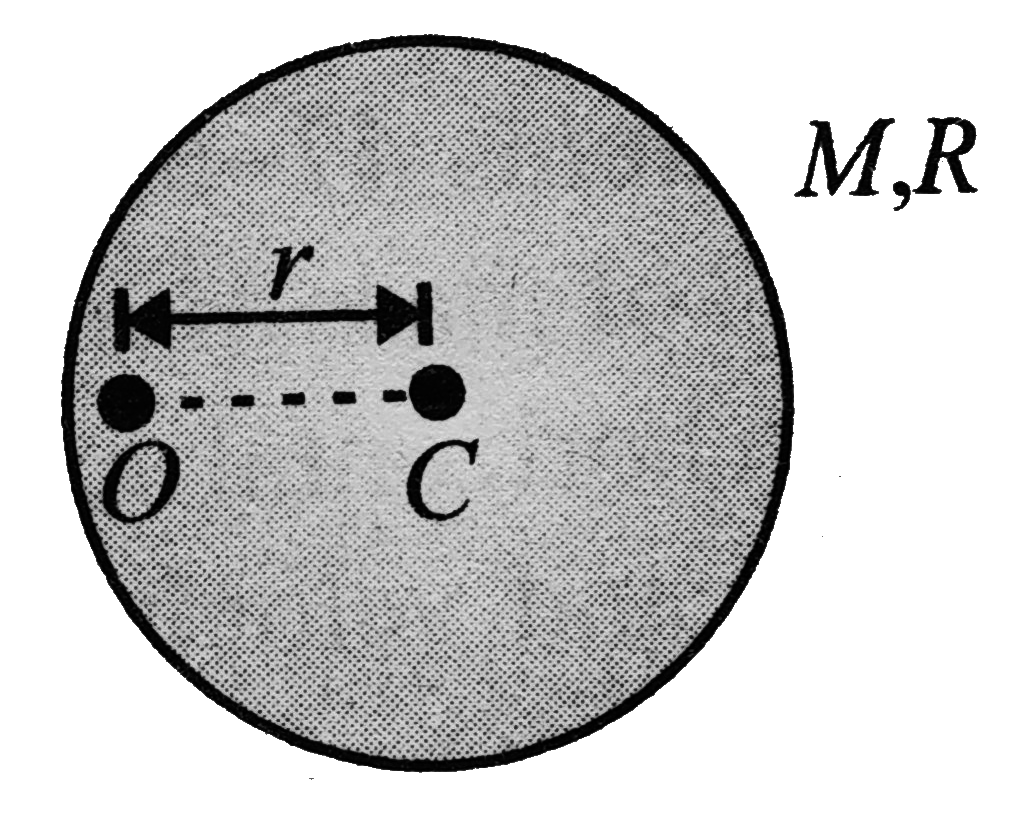
The angular velocity of the disc in the above described case is
View SolutionA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the centre of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ is
View Solution
