A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
During motion , Ngtmg
During motion, normal reactions acts on the center of mass
during motion, the normal reaction shifts towards positive x-axis from the center of mass
during motion, normal reaction shifts in the direction of the force of friction.
c) According to figure.

In this case, the force of friction has a tendency to rotate the cbe in clockwise directin. So, normal reaction will shift in forward direction to balance the torque due to force of friction.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives
9 Videos
- NEWTONS LAWS OF MOTION AND FRICTIONBOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives
23 Videos
- SCALARS AND VECTORSBOOK - BITSAT GUIDECHAPTER - SCALARS AND VECTORSEXERCISE - All Questions
34 Videos
Similar Questions
A uniform solid sphere of mass m and radius r = 3m is projected along a rough horizontal surface with the initial velocity v0=6m/s and angular ω0 velocity as shown in the figure. If the sphere finally comes to complete rest then angular velocity is x rad/s. Find x.

View SolutionIn each situation of column -I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown At t=0 (initially)the angular velocity of disc is omega_(0) and velocity of centre of mass of disc is v_(0) (in horizontal direction). The relation between v_(0) and ω0 and the initial sense of rotation is given for each situation in column-I then match the statement in column-I with the corresponding results in column-II.
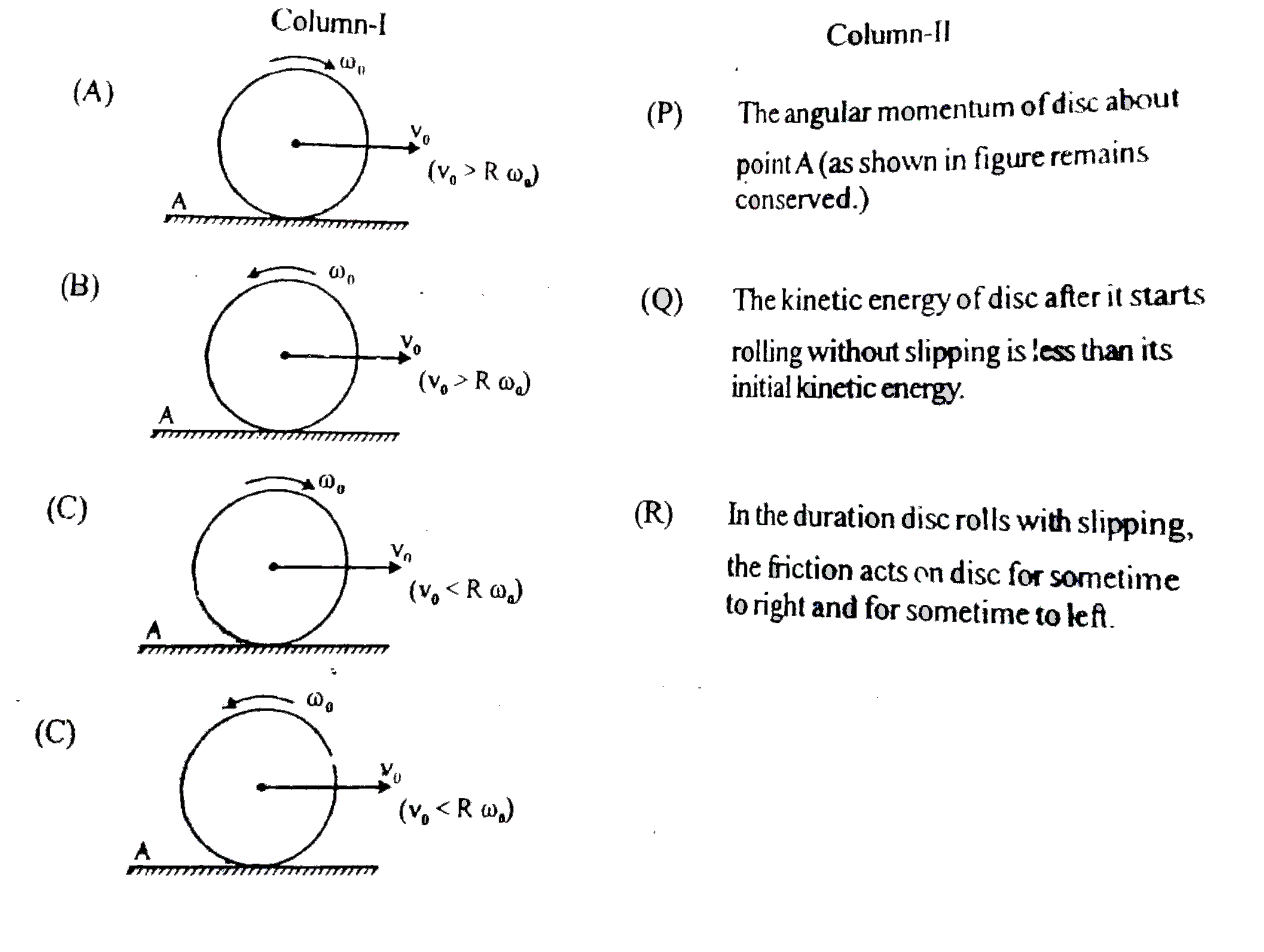
View Solution
Knowledge Check
A uniform rod of mass M and length L is moving on a smooth horizontal plane, such that its one end is moving with a velocity V0 and other end is moving with velocity 2V0 in the same direction as shown. Then which of the following is kinetic energy of the rod?
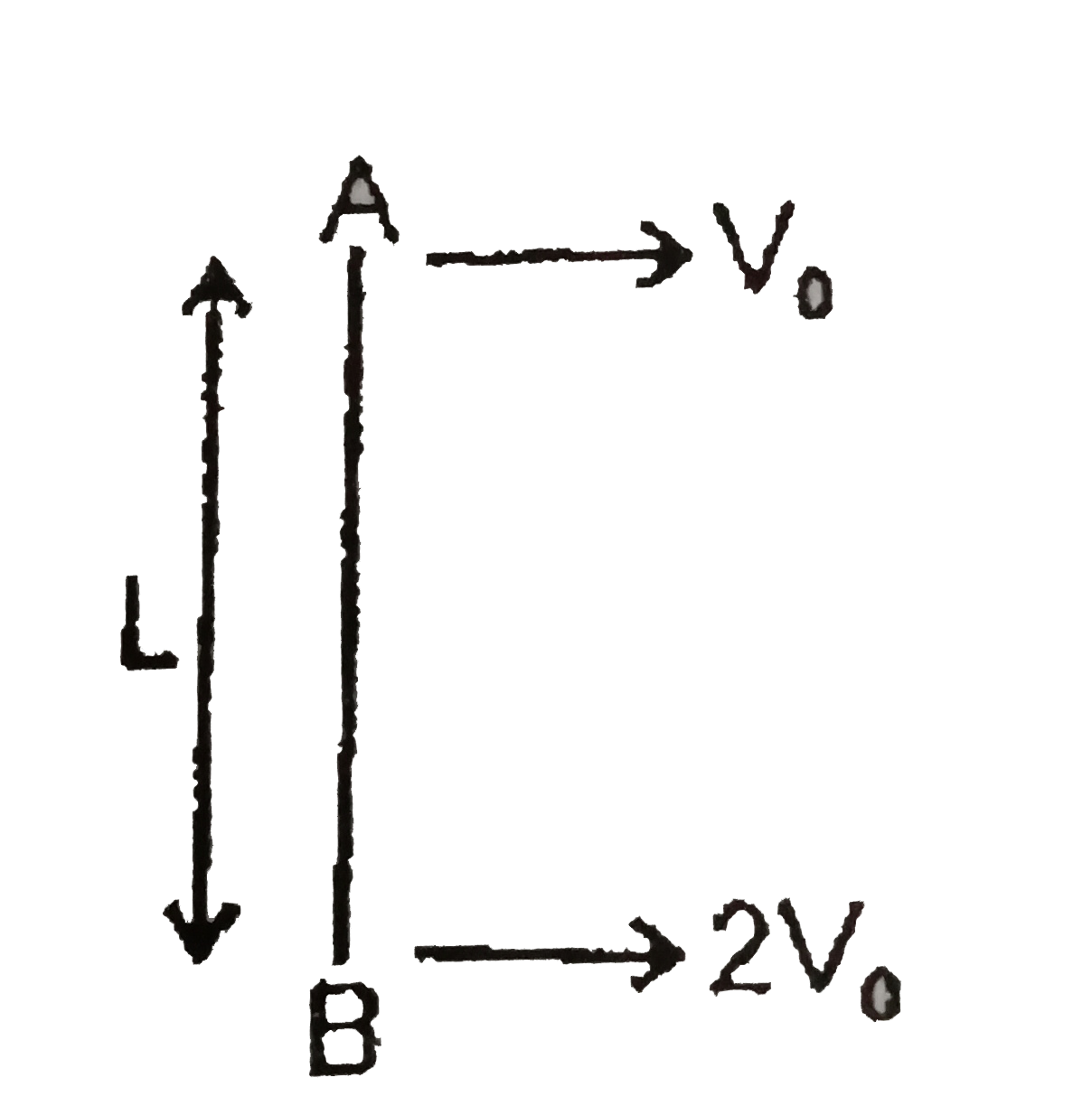 A132LMV20B2431MV20C76MV20D3124MV20
A132LMV20B2431MV20C76MV20D3124MV20A uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifAω0R=2V0Bω0R<2V0Cω0R>2V0DData insufficientThere is a uniform electric field of strength 103V/m along y-axis. A body of mass 1g and charge 10−6C is projected into the field from origin along the positive x-axis with a velocity 10m/s. Its speed in m/s after 10s is (Neglect gravitation)
A10B5√2C10√2D20
In each situation of Table-1, a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown. At, t=0 (initially) the angular velocity of disc is ω0 and velocity of centre of mass of disc is v0 (in horizontal direction). The relation between v0 and ω0 for each situation and also initial sense of rotation is given in Table-1 . Then match the statements in Table-1 with the corresponding results in Table-2.

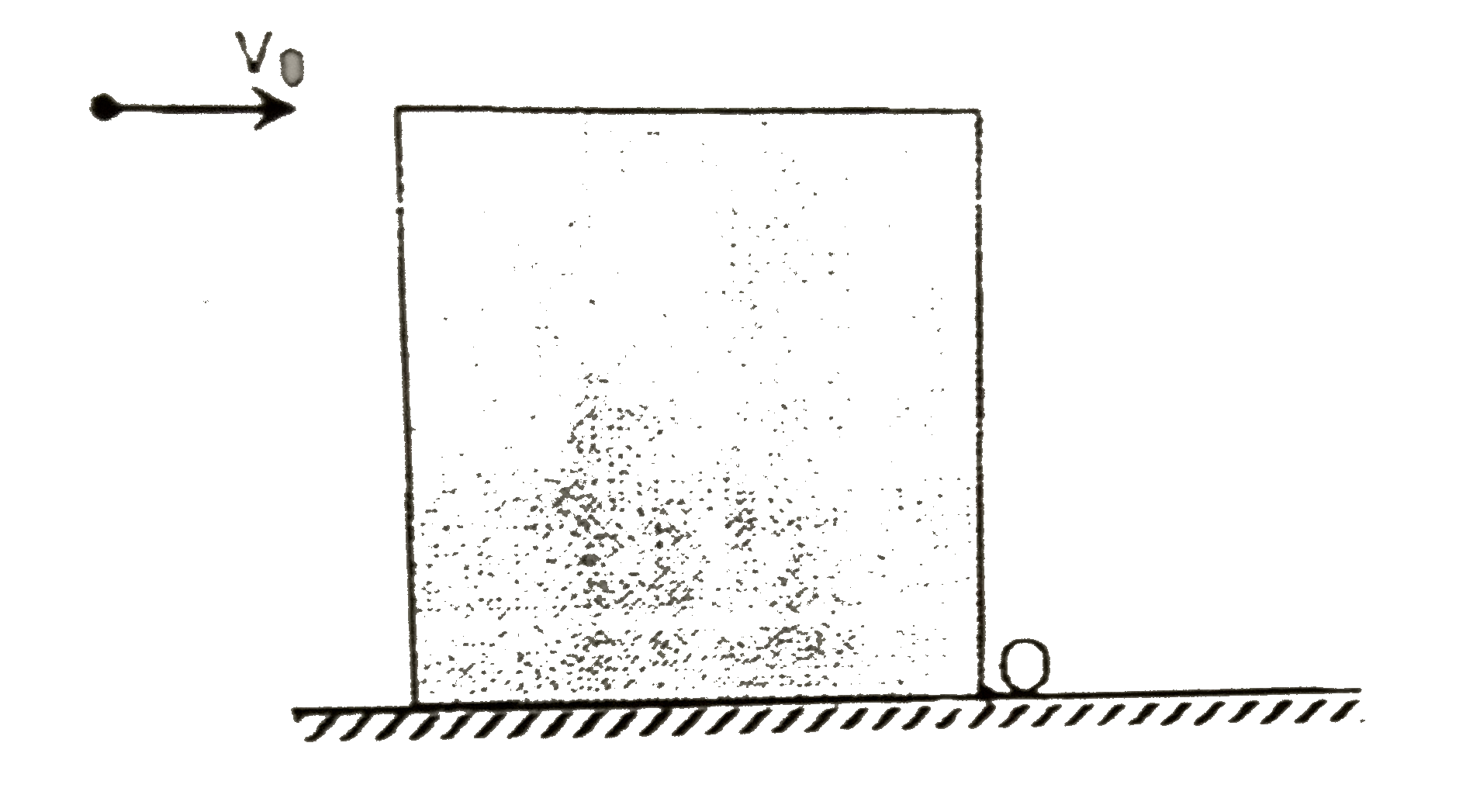
View SolutionIn the adjacent figure, a uniform cube of mass m and edge l=2m is lying at rest an a rough horizontal surface. A small ball of mass m hits the cbe at its top edge with horizontal speed v0 and sticks to it. Friction is so large that the cube can rotate about the edge 'O' without sliding. Calculate the minimum value of v0 ( in m/s) so that the cube will topple. Ignore any loss of energy due to friction at the edge O and take √2−1=0.4.
View SolutionA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision

View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View SolutionA small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of largen disc after collision is
View Solution
