A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
The correct Answer is:B, C
To solve the problem, we need to determine the minimum force F required to tip a uniform cube of side a and mass m about one of its edges when a horizontal force is applied at a height of 3a4 above the base.
1. Identify the Forces Acting on the Cube:
- The weight of the cube mg acts downwards at its center of mass, which is located at a height of a2 from the base.
- A horizontal force F is applied at a height of 3a4 above the base.
- There is also a normal force N acting upwards at the base of the cube.
2. Determine the Point of Rotation:
- The cube will begin to tip about the edge that is in contact with the table. We will consider the point of rotation to be at the edge of the cube.
3. Set Up the Torque Equation:
- The torque due to the force F about the point of rotation (the edge) is given by:
τF=F⋅(3a4)
- The torque due to the weight mg about the same point is given by:
τmg=mg⋅(a2)
4. Condition for Tipping:
- The cube will start to tip when the torque due to the applied force F is equal to the torque due to the weight of the cube:
F⋅(3a4)=mg⋅(a2)
5. Solve for F:
- Rearranging the equation gives:
F=mg⋅(a2)(3a4)
- Simplifying this expression:
F=mg⋅23=2mg3
6. Conclusion:
- The minimum value of the force F required to tip the cube is:
F=2mg3
- The weight of the cube mg acts downwards at its center of mass, which is located at a height of a2 from the base.
- A horizontal force F is applied at a height of 3a4 above the base.
- There is also a normal force N acting upwards at the base of the cube.
- The cube will begin to tip about the edge that is in contact with the table. We will consider the point of rotation to be at the edge of the cube.
- The torque due to the force F about the point of rotation (the edge) is given by:
τF=F⋅(3a4)
- The torque due to the weight mg about the same point is given by:
τmg=mg⋅(a2)
- The cube will start to tip when the torque due to the applied force F is equal to the torque due to the weight of the cube:
F⋅(3a4)=mg⋅(a2)
- Rearranging the equation gives:
F=mg⋅(a2)(3a4)
- Simplifying this expression:
F=mg⋅23=2mg3
- The minimum value of the force F required to tip the cube is:
F=2mg3
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
A uniform cube of side a & mass m rests on a rough horizontal table as shown. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a4 above the base. The minimum value of F for which the cube begins to tip about an edge is αmgβ. Find (a (aβ) (assume that cube does not slide).
'(##CEN_KSR_PHY_JEE_C09_E01_028_Q15##)'
View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.
View Solution
Knowledge Check
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
Amg4B2mg3C3mg4DmgA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
AmgBmg3C2mg3D5mg3A uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
A14mgB2mgC12mgD23mg
A cubical block of side a and of mass m rests on a rough horizontal surface. A horizontal force F is applied to normal to one of the faces at height h above the base h>a/2. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA unifrom cube of mass m and side a is placed on a frictionless horizontal surface .A vertical force F is applied to the edge as shown in figure ,match the following (most appropriate choice )

View SolutionA uniform cube of side 'b' and mass M rest on a rough horizontal table. A horizontal force F is applied normal to one of the face at a point, at a height 3b/4 above the base. What should be the coefficient of friction (μ) between cube and table so that is will tip about an edge before it starts slipping ?
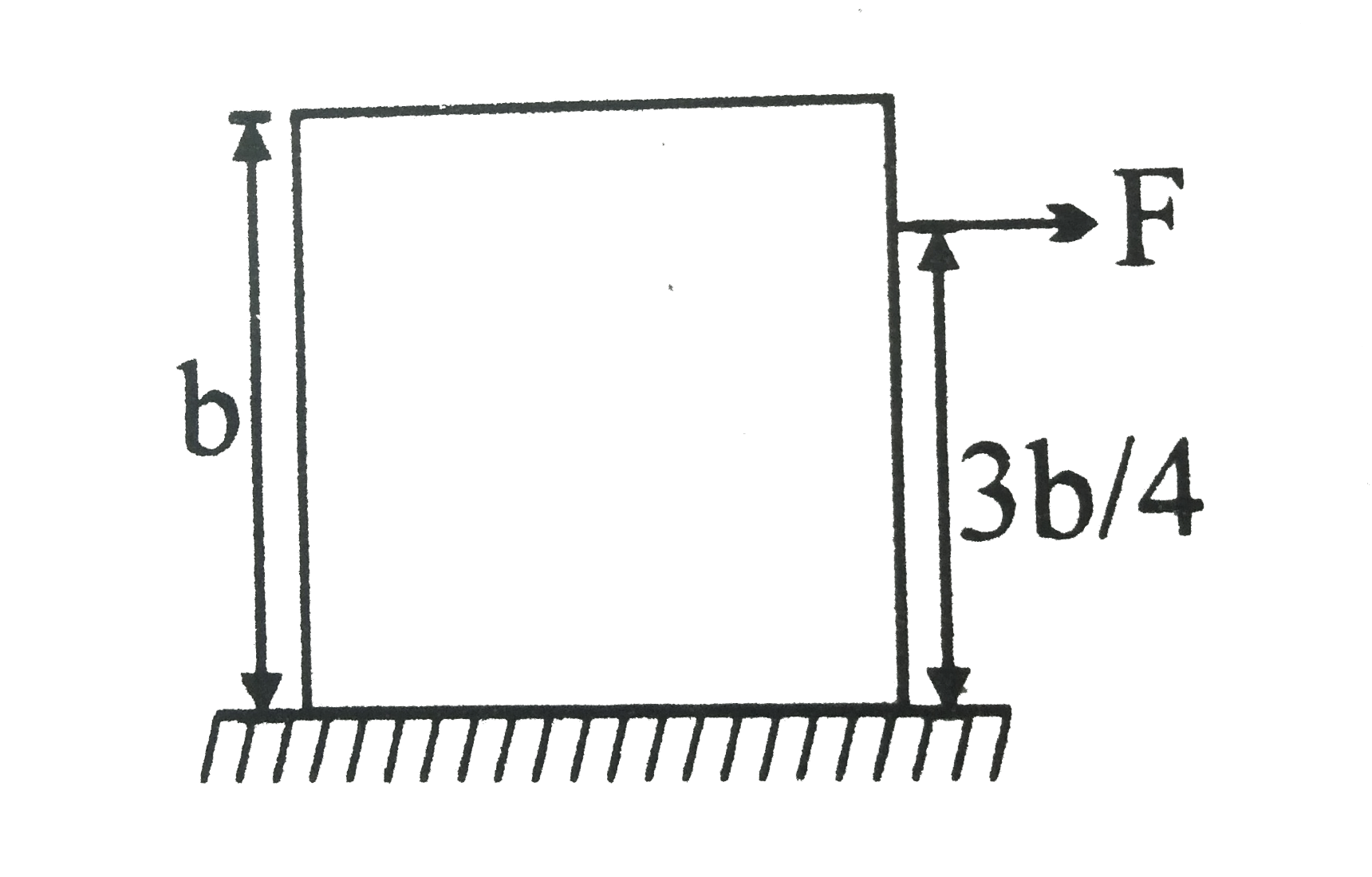 .
.
View SolutionIf the friction is sufficient to prevent the block from sliding, then the minimum value of F for which the cube begins to topple about an edge is
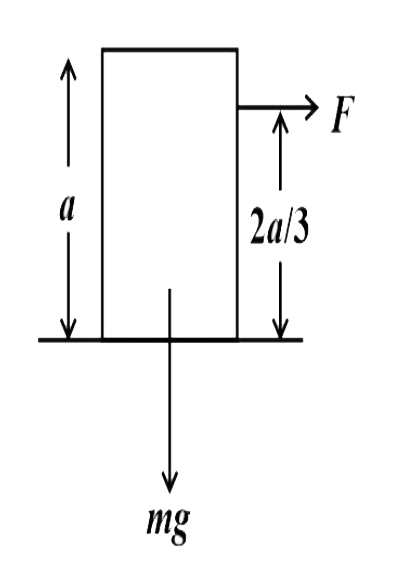
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View Solution
