A uniform disc of mass and radius is projected horizontally with velocity on a rough horizontal floor so that it starts off with a purely sliding motion at . After seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at .
Assuming that the coefficent of friction to be , calculate .

of the disc.
When the disc is projected it starts sliding and hence there is a relative motion between the points of contact. Therefore frictioal force acts on the disc in the direction opposite to the motion.

a. Now for translational motion
(as it slides )
negative sign indicates that is opposite to
, where ...........i
For rotational motion about centre.
......ii
Therefore , using
...........iii
Using i using iii
b. Putting the value of in eqn i we get
c. Work done by the frictional force is equal to change in
d. For time work done by the friction is Zero.
Therefore for longer time total work done is same and that in part c.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View Solution
A disc of mass M and radius R is rolling purely with centre's velcity v0 on a flat horizontal floor when it hits a step in the floor of height R/4 The corner of the step is sufficiently rough to prevent any slippoing of the disc against itself. What is the velocity of the centre of the disc just after impact?View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then
 View Solution
View SolutionA uniform disc is having a pure rolling motion on a moving plank as shown in the figure. Choose the correct option among the following .
 View Solution
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
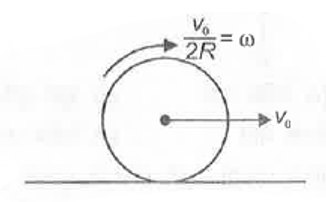 View Solution
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
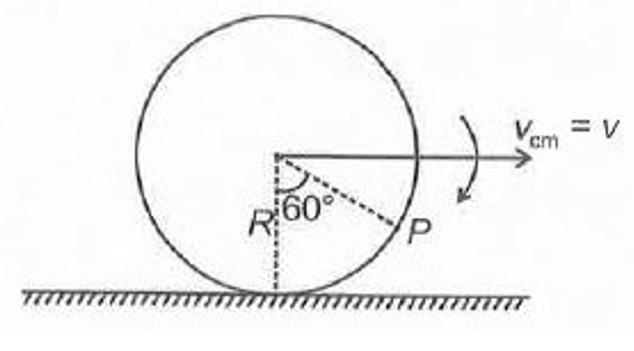 View Solution
View SolutionThe velocity of a point P on the surface of a pure rolling disc as shown in figure, can be calculated as given below.
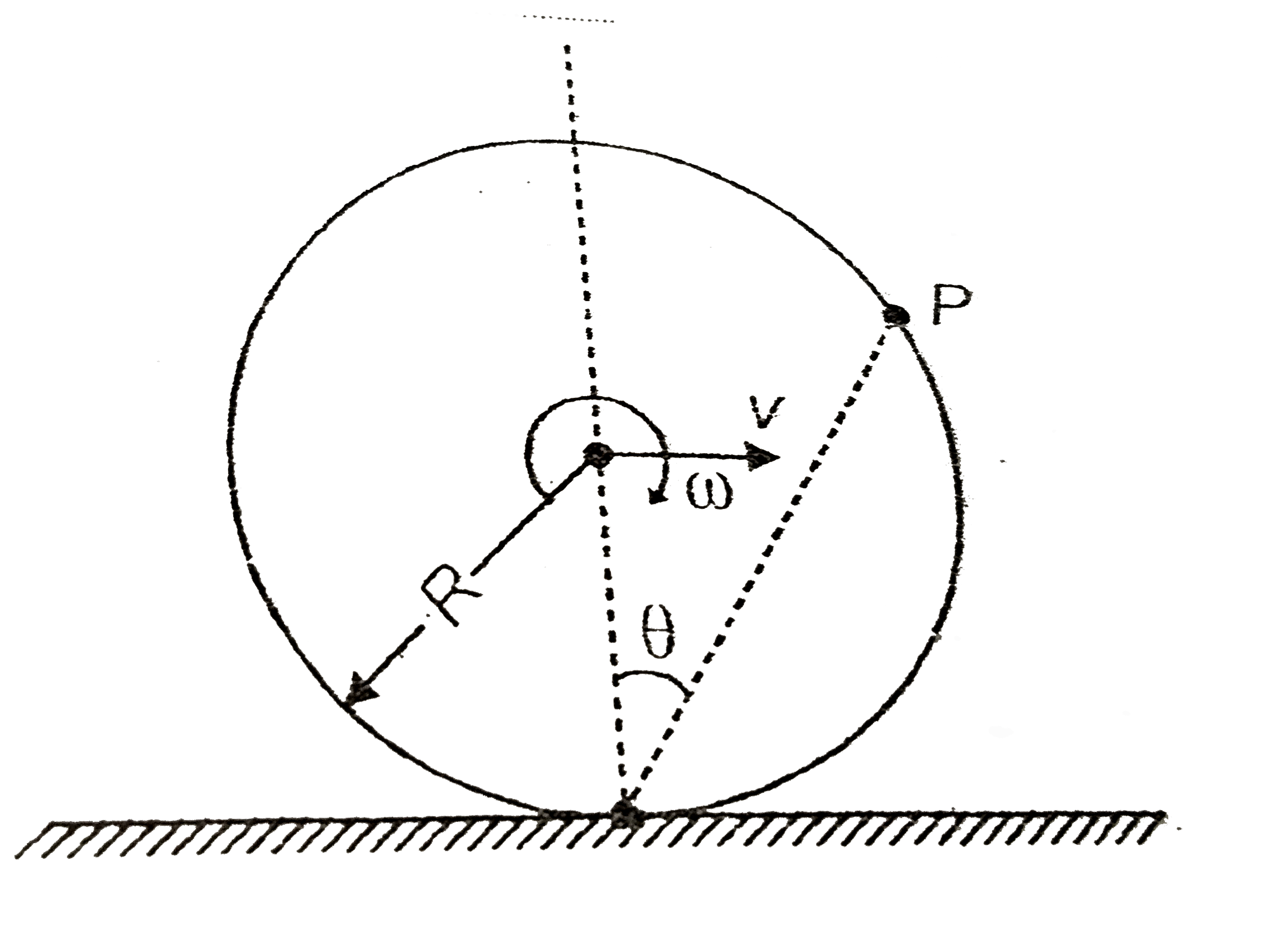 View Solution
View SolutionA uniform disc of mass m and radius R is thrown on horizontal lawn in such a way that it initially slides with speed V0 without rolling. The distance travelled by the disc till it starts pure rolling is (Coefficient friction between the contact is 0.5)
View Solution
