A uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
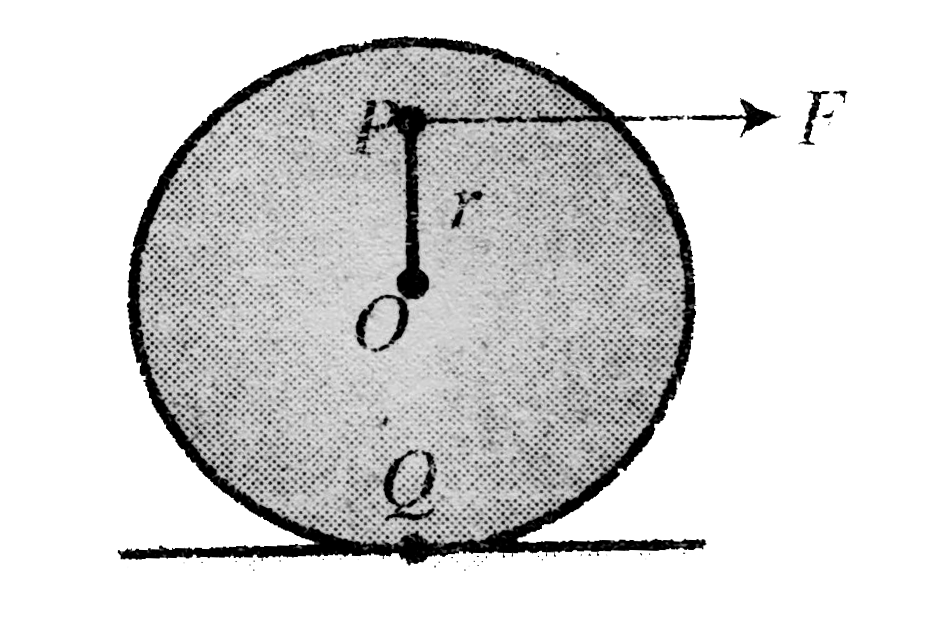
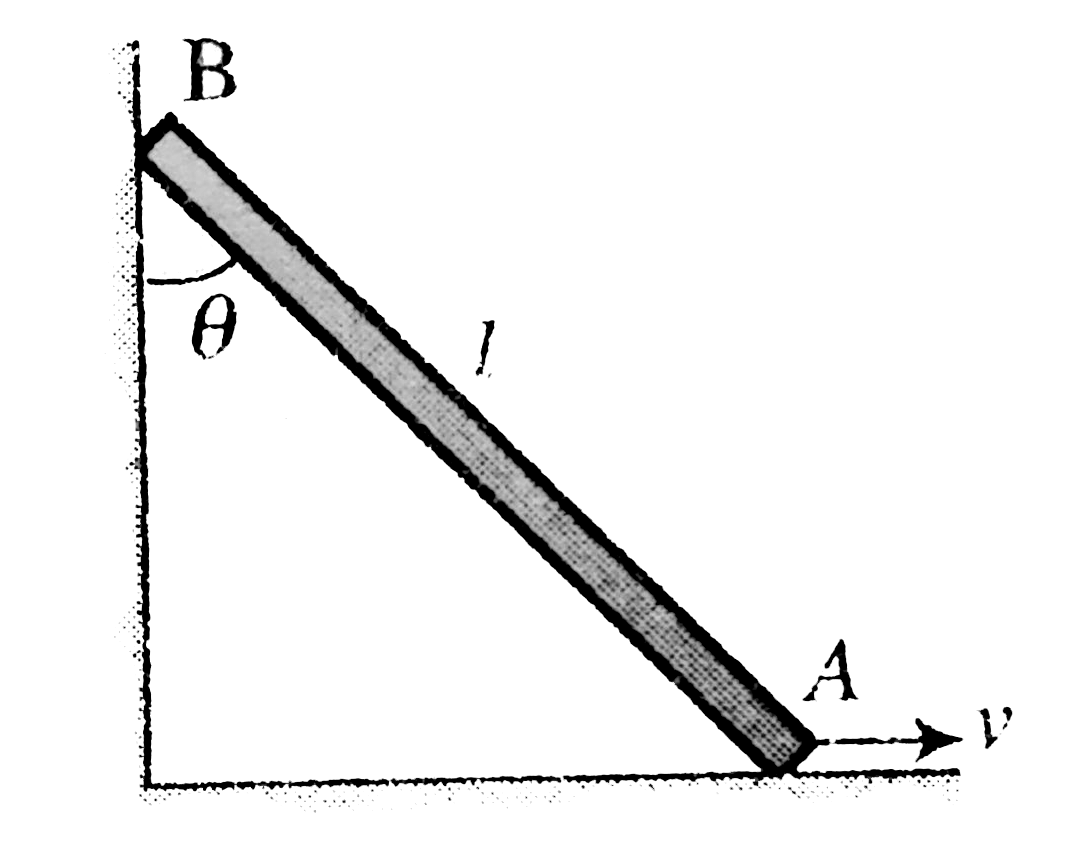
A rod of length l=1m leaning against a vertical wall is pulled at its lowest point A with a constant velocity v=4ms−1. In consequence, the rod rotates win the vertical plane. When the rod makes an angle θ=4ms−1 with vertical and find the angular velocity of the rod (in rads−1).
The correct Answer is:5
From the geometry of the arranement we observe that the ends A and B side on the horizontal and vertical surfaces with velocities vA and vB respectively, where vA=v (given) and vB is assumed. As per the procedure, let us drop perpediculars AX and BY from A and B respectively onto their lines of motion (→vA and →vB). We observe that the perpendicular intersect at P. Then P is the instantaneous axis of rotation.
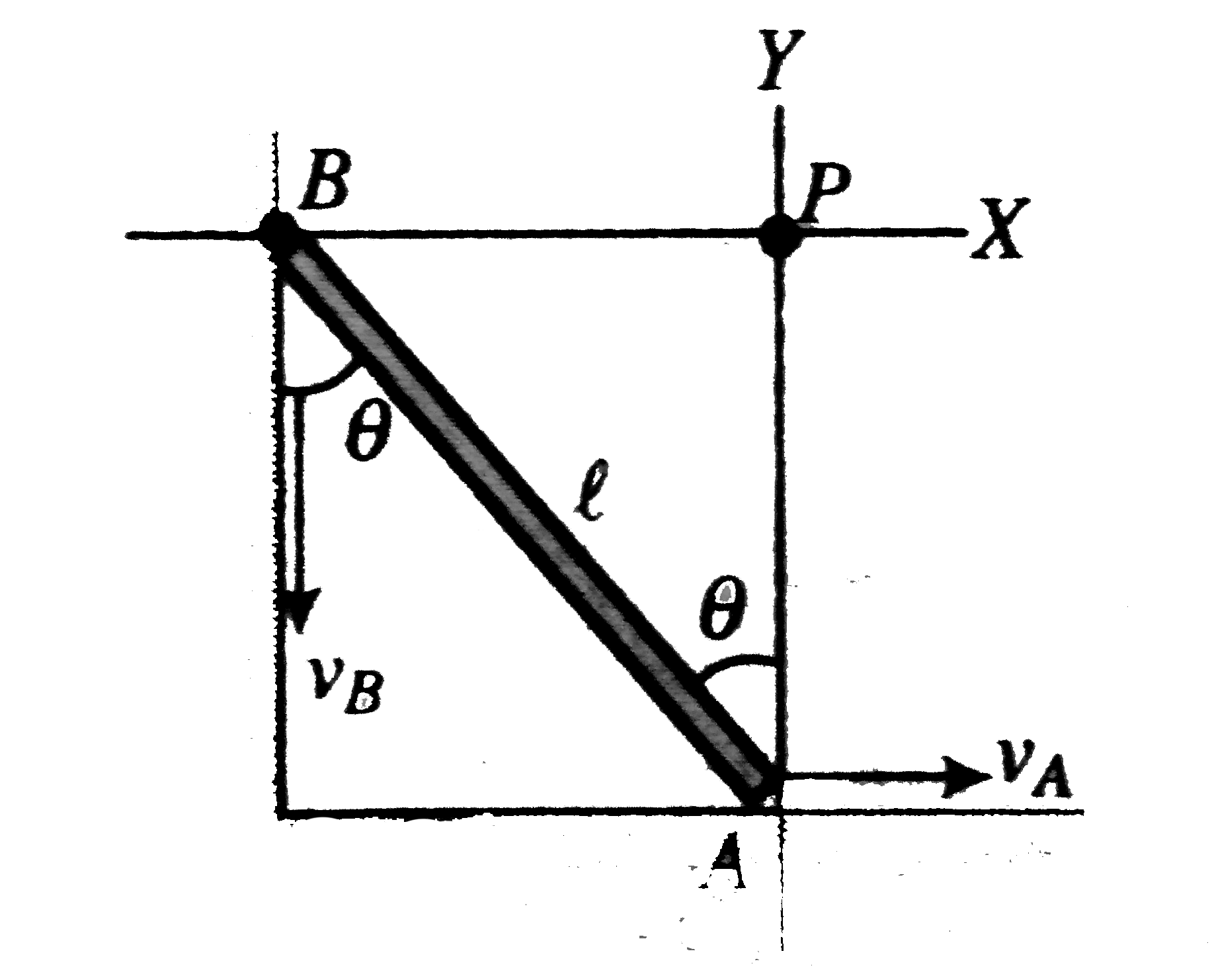
Since vP=0
we have ωBP=ωAP(=ω)
substituting PA=lcosθ and vA=v
We have ω=vcosθ=41.45=5rads−1
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:

acceleration of the CM (in ms2)
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:

acceleration of the CM (in ms2)
View Solution
Knowledge Check

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3mA hollow cylinder of mass m and radius r is kept on a smooth horizontal surface. Horizontal force F is applied at a height above the centre. Find the value of h/R so that ring performs pure rolling on the surface.
A1B12C13D25
A uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
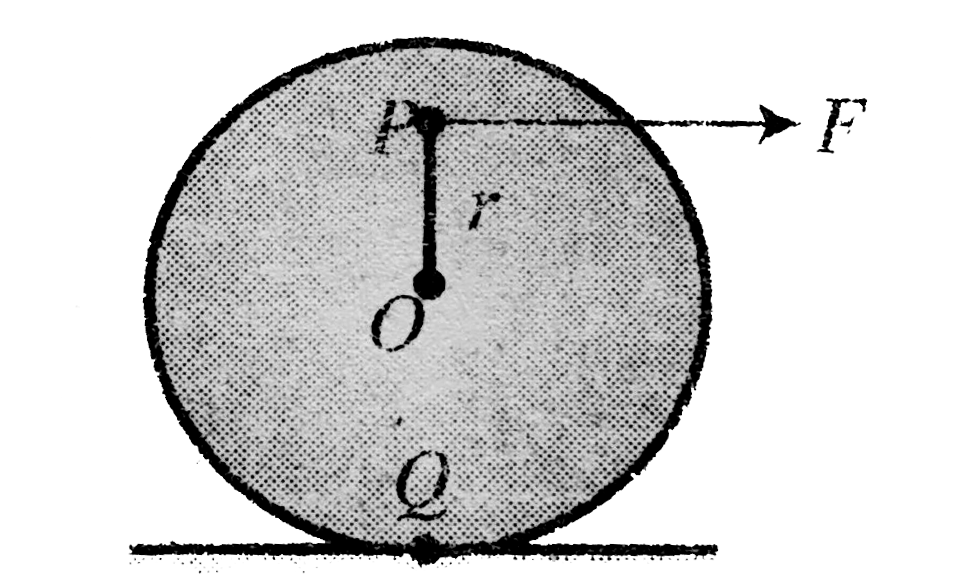
angular acceleration of the disc. (rads−1)
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
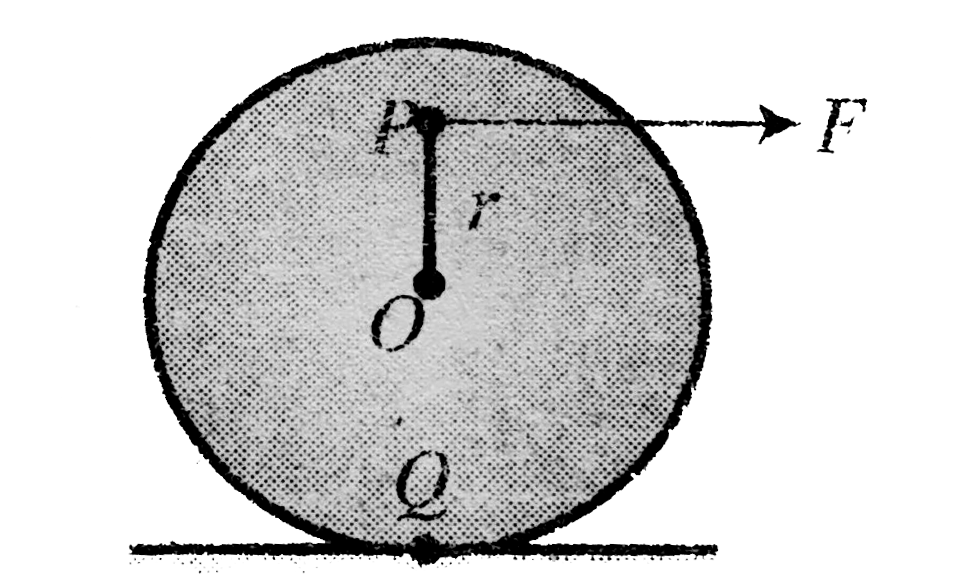
angular acceleration of the disc. (rads−1)
View SolutionThree identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
View Solution
