A uniform electric field exists in x−y plane. The potential of points A(−2m,2m),B(−2m,2m) and C(2m,4m) are 4V,16V and 12V respectively. The electric field is
(4ˆi+5ˆj)Vm
(3ˆi+4ˆj)Vm
−(3ˆi+4ˆj)Vm
(3ˆi+4ˆj)Vm
The correct Answer is:D
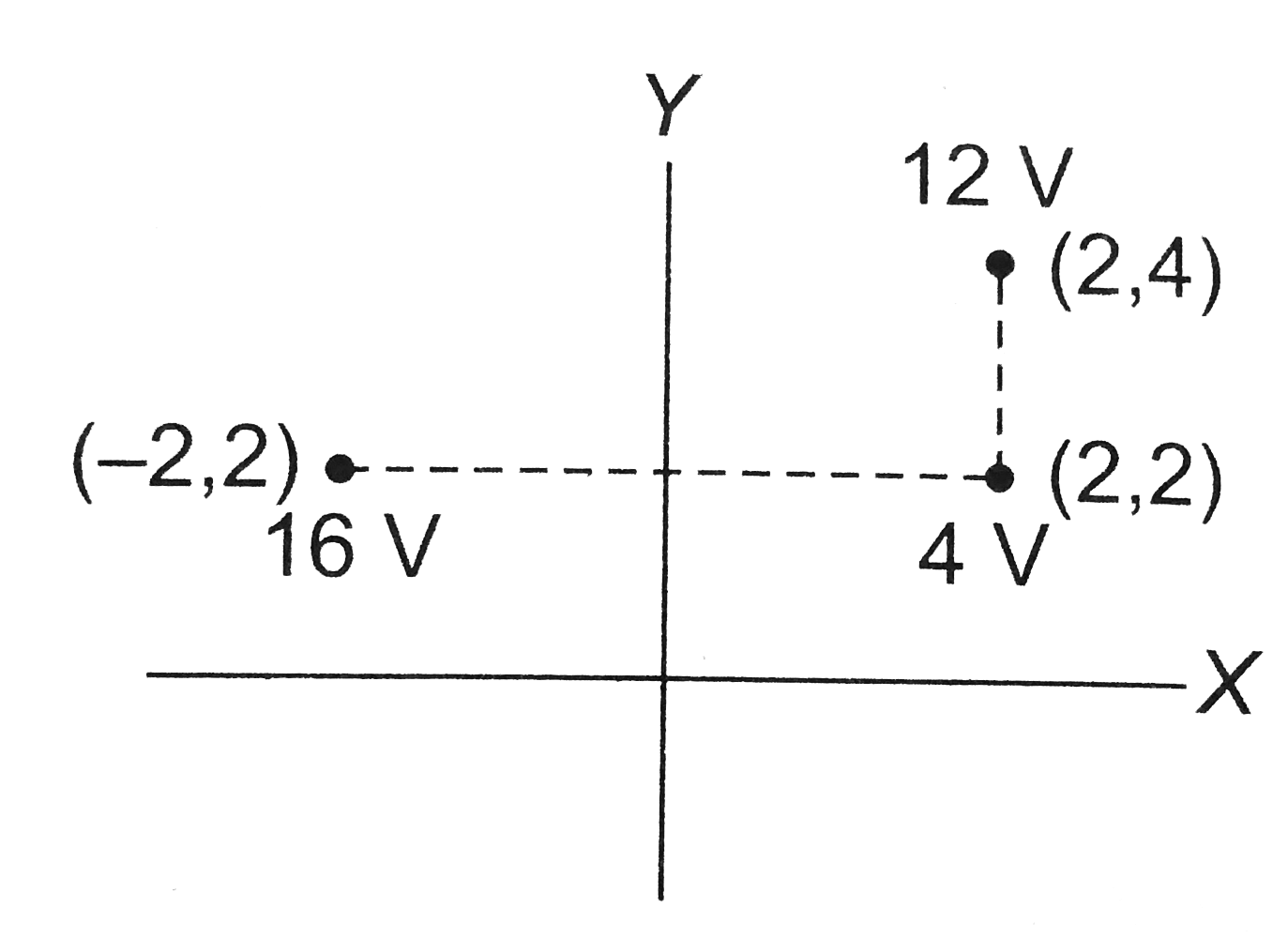
→Ex=16−42ˆi=3ˆi
→Ey=−12−42ˆj=−4ˆj
→E=(3ˆi−4ˆj)Vm−1
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Euipotentials
45 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A uniform electric field is along x-axis. The potential difference VA−VB=10V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionTwo point charges of, 1 μC and -1 μC are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View Solution
Knowledge Check
A uniform electric field exists in x-y plane. The potential of points A(2m,2m),B(−2m,2m) and C(2m,3m) are 4V,16V and 12V respectively. The electric field is
A(4ˆi+5ˆj)V/mB(3ˆi+4ˆj)V/mC−(3ˆi+4ˆj)V/mD(3ˆi−4ˆj)V/mTwo particle A and B of masses mA and mB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in the figure. Then-
 AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vB
AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vBFind the potential difference VAB between A(2m,1m,0) and B(0,2m,4m) in an electric field,
E=(xˆi−2yˆj+zˆk)VmA2VB5VC3VD4V
A uniform electric field of 30NC−1 exists along the X-axis calculate the potential difference VB−VA between the points A (4m,2m) and B(10m,5m).
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionAn electric charge 10−8C is placed at the point (4m, 7m, 2m). At the point (1m, 3m, 2m), the electric :
View SolutionAn electric field →E=ˆiCx exists in the space, where C = 10 V/m2 . Taking the potential at (10 m, 20 m ) to be zero, find the potential at the origin.
View SolutionAn electric charge 10−8C is placed at the point (4m,7m,2m). At the point (lm,3m,2m,), the electric.
View Solution
