A uniform magnetic field is restricted with a region of radius r. The magnetic field change with time at a rate −−→dBdt. Loop 1 of radius R>r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in the figure below. then the e.m.f. genrated is
]
−−→dBdtπR2 in loop 1 and zero in loop 2
−−→dBdtπr2 in loop 1 and zero in loop 2
zero in loop 1 and zero in loop 2
−−→dBdtπR2 in loop 1 and −→dBdt0πr2 in loop 2
The correct Answer is:B
For loop 1
eind=−A(d→Bdt)cos0∘=−πr2(d→Bdt)
for loop 2,eind=0 has no flux linkage
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - AIIMS Questions
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B - Assertion Reasoning
31 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
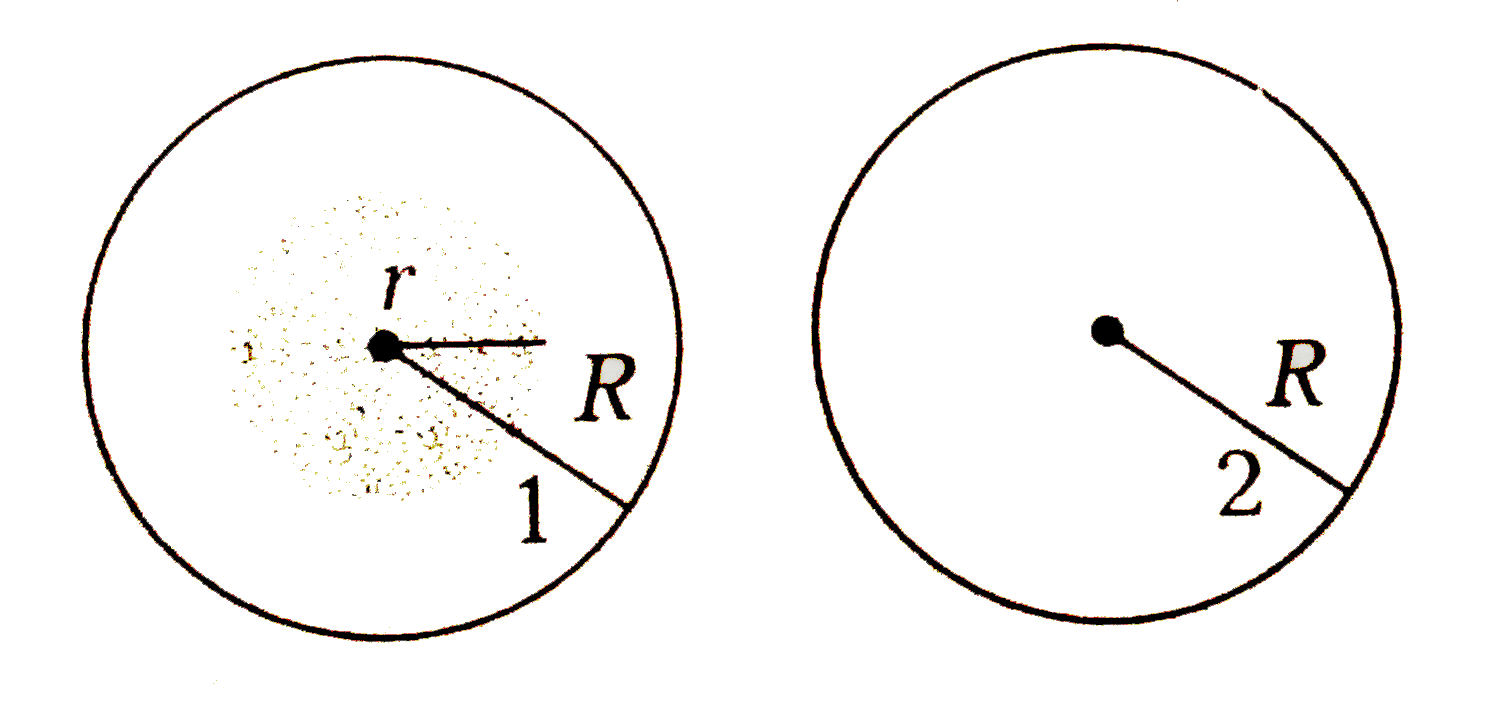
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View SolutionA uniform magnetic field is restricted within a region of radius 1m. The magnetic field changes with time(t) as →B=B0(2t3)ˆk. A loop of radius 2m is outside the region of magnetic field as shown in figure. The emf induced in loop is
_PHY_E06_055_Q01.png)
View Solution
Knowledge Check
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
 A−d→BdtπR2 in loop 1 and zero in loop 2B−d→Bdtπr2 in loop 1 and zero in loop 2CZero in loop 1 and zero in loop 2D−d→Bdtπr2 in loop 1 and −d→Bdtπr2 in loop 2
A−d→BdtπR2 in loop 1 and zero in loop 2B−d→Bdtπr2 in loop 1 and zero in loop 2CZero in loop 1 and zero in loop 2D−d→Bdtπr2 in loop 1 and −d→Bdtπr2 in loop 2A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
 AZero in loop 1 and zero in loop 2B−dBdtπr2 in loop 1 and −dBdtπ2 in loop 2C−dBdtπR2 in loop 1 and zero in loop 2D−dBdtπr2 in loop 1 and zero in loop 2
AZero in loop 1 and zero in loop 2B−dBdtπr2 in loop 1 and −dBdtπ2 in loop 2C−dBdtπR2 in loop 1 and zero in loop 2D−dBdtπr2 in loop 1 and zero in loop 2Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.
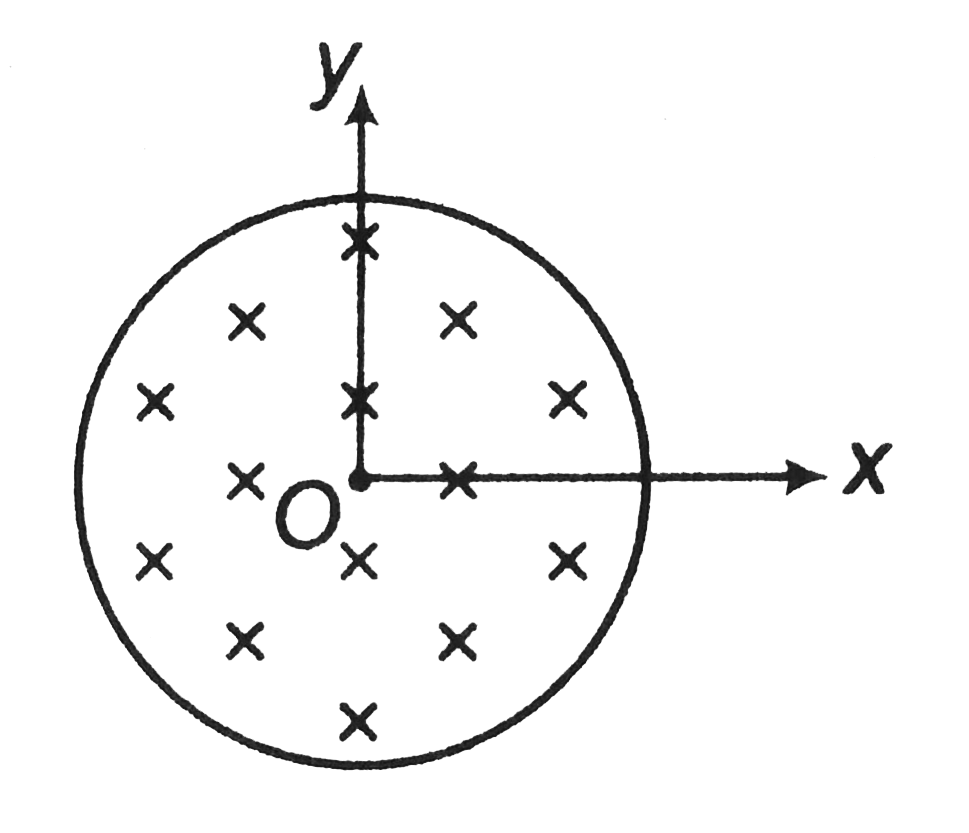 Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axis
Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axis
A uniform magnetic field is restricted within a region of radius 1m. The magnetic field changes with time(t) as →B=B0(2t3)ˆk. A loop of radius 2m is outside the region of magnetic field as shown in figure. The emf induced in loop is
_PHY_E06_055_Q01.png)
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionThe flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png)
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.

View Solution
