A uniform magnetic field of 1.5T exists in a cylinderical region of radius 10.0 cm, its direction being parallel to the axis along east to west. A current carrying wire in north-south direction passes through this region. The wire intersects the axis and experience a force of 1.2N downwards. If the wire is turned from north south to northest-southwest direction. then magnitude and direction of force is
1.2 N, upward
1.2√2, downward
1.2N, downward
1.2√2N, downward
The correct Answer is:c
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the Initial Setup
We have a uniform magnetic field of 1.5 T directed from east to west. A current-carrying wire is oriented in the north-south direction and experiences a downward force of 1.2 N.
Hint: Visualize the magnetic field and the wire's orientation to understand how they interact.
Step 2: Determine the Force on the Wire
The force on a current-carrying wire in a magnetic field is given by the formula:
F=I⋅B⋅L⋅sin(θ)
where:
- F is the force,
- I is the current,
- B is the magnetic field strength,
- L is the length of the wire in the magnetic field,
- θ is the angle between the magnetic field and the current direction.
Initially, since the wire is in the north-south direction and the magnetic field is east-west, the angle θ is 90 degrees. Thus, sin(90∘)=1.
Step 3: Calculate the Current
From the initial force:
F=I⋅B⋅L
Given F=1.2N and B=1.5T, we can express the current:
1.2=I⋅1.5⋅L
This implies:
I⋅L=1.21.5=0.8
Step 4: Change the Wire Orientation
Now, the wire is turned from the north-south direction to the northeast-southwest direction. This means the angle θ between the magnetic field and the current direction is now 45 degrees.
Step 5: Calculate the New Force
Using the same formula for the force with the new angle:
F′=I⋅B⋅L⋅sin(45∘)
Since sin(45∘)=√22, we have:
F′=I⋅B⋅L⋅√22
Step 6: Substitute the Current Value
We already found I⋅L=0.8:
F′=0.8⋅1.5⋅√22
Calculating this gives:
F′=0.8⋅1.5⋅0.7071≈0.848N
Step 7: Determine the Direction of the Force
To find the direction of the force, we can use the right-hand rule. Curl your fingers from the direction of the current (northeast-southwest) towards the direction of the magnetic field (east-west). The thumb will point in the direction of the force.
Since the wire is now oriented at 45 degrees, the force will still be directed downwards, but the magnitude will be less than the initial force.
Final Result
The magnitude of the force when the wire is turned to the northeast-southwest direction is approximately 0.848 N, and the direction of the force remains downwards.
---
We have a uniform magnetic field of 1.5 T directed from east to west. A current-carrying wire is oriented in the north-south direction and experiences a downward force of 1.2 N.
The force on a current-carrying wire in a magnetic field is given by the formula:
F=I⋅B⋅L⋅sin(θ)
where:
- F is the force,
- I is the current,
- B is the magnetic field strength,
- L is the length of the wire in the magnetic field,
- θ is the angle between the magnetic field and the current direction.
From the initial force:
F=I⋅B⋅L
Given F=1.2N and B=1.5T, we can express the current:
1.2=I⋅1.5⋅L
This implies:
I⋅L=1.21.5=0.8
Now, the wire is turned from the north-south direction to the northeast-southwest direction. This means the angle θ between the magnetic field and the current direction is now 45 degrees.
Using the same formula for the force with the new angle:
F′=I⋅B⋅L⋅sin(45∘)
Since sin(45∘)=√22, we have:
F′=I⋅B⋅L⋅√22
We already found I⋅L=0.8:
F′=0.8⋅1.5⋅√22
Calculating this gives:
F′=0.8⋅1.5⋅0.7071≈0.848N
To find the direction of the force, we can use the right-hand rule. Curl your fingers from the direction of the current (northeast-southwest) towards the direction of the magnetic field (east-west). The thumb will point in the direction of the force.
The magnitude of the force when the wire is turned to the northeast-southwest direction is approximately 0.848 N, and the direction of the force remains downwards.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
An electric current flows in a wire from north to south.
What will be the direction of the magnetic field due to this wire at a point.
View SolutionA magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm as shown in . A wire, carrying a current of 2.0 A, is placed perpendiuclar to and intersecting the axis of the cylindreical region. Find the magnitude of the force acting on the wire.
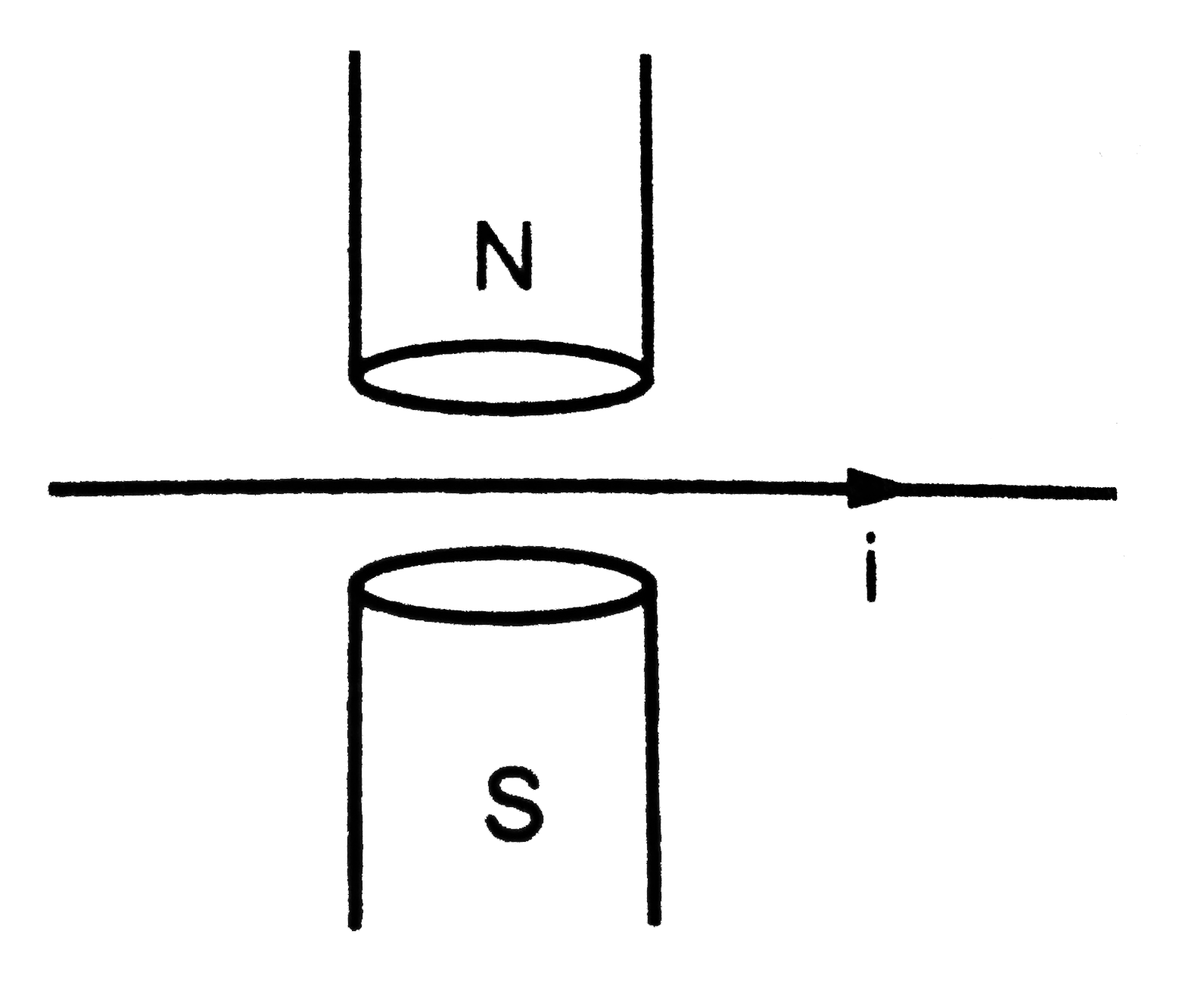
View Solution
Knowledge Check
A long straight wire in the horizontal plane carries as curret of 75 A in north to south direction, magnitude and direction of field B at a point 3 m east of the wire is
A4×10−6T, vertical upB5×10−6T, vertical downC5×10−6T, vertical upD4×10−6T, vertical down
A current carrying wire is placed along east and west in a magnetic field directed north wards. If the current in the wire is directed east wards, the direction of force on the wire is
View SolutionA long straight wire in the horizontal plane carries a current of 50A in north to south direction. Give the magnitude and direction of →B at a point 2⋅5m east of the wire.
View Solutiona vertical wall is in South north direction. a current carrying where is kept in the world such that to the west of the wall magnetic field due to wire is towards south then the wire where should be
View SolutionTwo parallel wires separated by a distance of 10cm carry currents of 10 A and 40 A along the same direction, Where should a third current be placed so that it experience no magnetic force?
View SolutionA wire placed along north-south direction carries a current of 10 A from south to north. Find the magnetic field due to a 1 cm piece of wire at a point 200cm north-east from the piece.
View SolutionThe cube as shown in Fig. 1.61, 75.0 cm on a side, is placed in a uniform magnetic field of 0.860 T parallel to the x-axis. The wire abcdef carries a current of 6.58 A in the direction indicated.
(a) Determine the magnitude and direction of the force acting on the segment ab.
(b) Determine the magnitude and direction of the force acting on the sement bc.
(c) Determine the magnitude and direction of the force acting on the segment cd.
(d) Determine the magnitude and direction of the force acting on the segment de.
(e) Determine the magnitude and direction of the force acting on the segment ef.
(f) What are the magnitude and direction of the total force on the wire ?

View SolutionA current canying straight wire is placed along east-west and current is passed through it eastward . The direction of the force act on it due to horizontal component of earth's magnetic field is
View Solution
