A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

The correct Answer is:A, B
At P1 gravitatioN/Al field due to sphere M
=GM(3a+a)2=GM16a2
ATP2 GravitatioN/Al field is due to sphere and shell
=(GM)/((a+4a+a)^2) (GM)/((4+a)^2)<br>=(GM)/(36a^2)+(GM)/(25a^2)<br>=(GM)/a^2(1/36+1/25)e<br>GMa2(25+36900)=(61900)GMa2

Topper's Solved these Questions
Similar Questions
A force F acts at the centre of a thin spherical shell of mass m and radius R.
Find the acceleration of the shell if the surface is smooth.
View SolutionA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View Solution
Knowledge Check
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
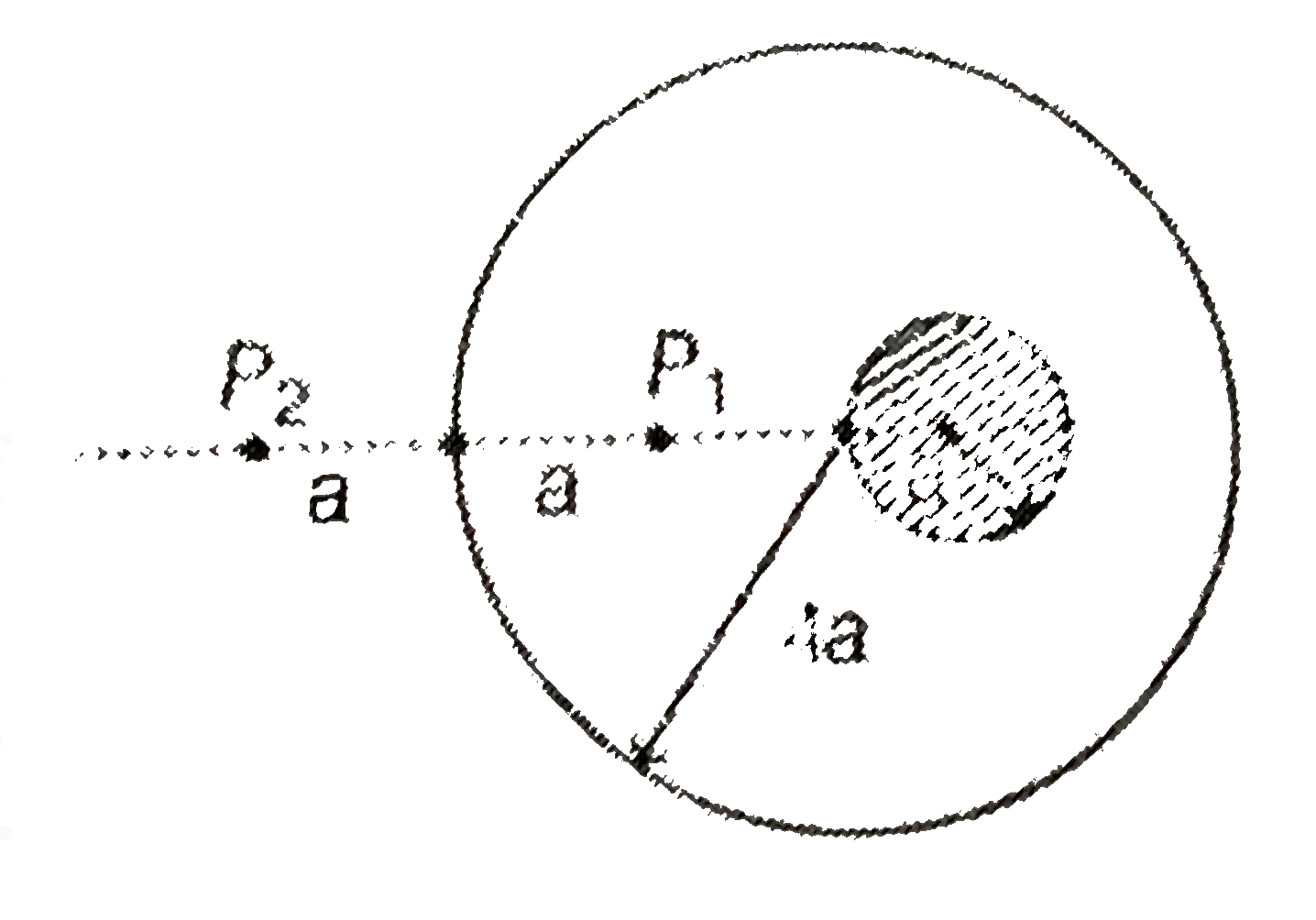 AThe gravitational field intensity at P1 is GM16a2BThe gravitational field intensity at P2 is 61GM900a2CThe gravitational potential at P1=0DThe gravitational potential at P2=0
AThe gravitational field intensity at P1 is GM16a2BThe gravitational field intensity at P2 is 61GM900a2CThe gravitational potential at P1=0DThe gravitational potential at P2=0Consider a thin spherical shell of uniform density of mass M and radius R:
AThe gravitational field inside the shell will be zeroBThe gravitational self energy of shell is GM22RCAttractive force experience by unit area of the shell pull the other half is GM22R2DNet gravitational force with which one hemisphere of the shell arracts other, is GM28R2A uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
AThe gravitational field at a distance of 1.5r from the centre is 29Gmr2BThe gravitational field at a distance of 2.5r from centre is 825Gmr2CThe gravitational field at a distance of 1.5r from centre is zeroDThe gravitational field between the sphere and spherical shell is uniform.
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
View SolutionA solid sphere of radius a and mass m is surrounded by cocentric spherical shell of thickness 2a and mass 2m the gravitational field at a distance 3a from their centres is
View SolutionA uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass is kept at a distance x(>R) in the region bounded by spheres as shown in the figure . The net gravitational force on the particle is

View SolutionConsider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View Solution
