A uniform metallic rod PQ of length 2 m is acted upon by two forces A and B along the directions as shown in the figure. Find the magnitude and position of the resultant normal force that acts on the rod.

Video Solution

Text Solution

Verified by Experts

The forces that act normally to the rod are
$A {cos 60}^{\circ} = 90 \times \frac{1}{2} = 45 N$
$B {cos 60}^{\circ} = 30 \times \frac{1}{2} = 15 N$ .
As the two forces are unlike parallel forces, the resultant of these two forces is outside the rod at a point 'O' and in the direction of greater force, i.e. , A.

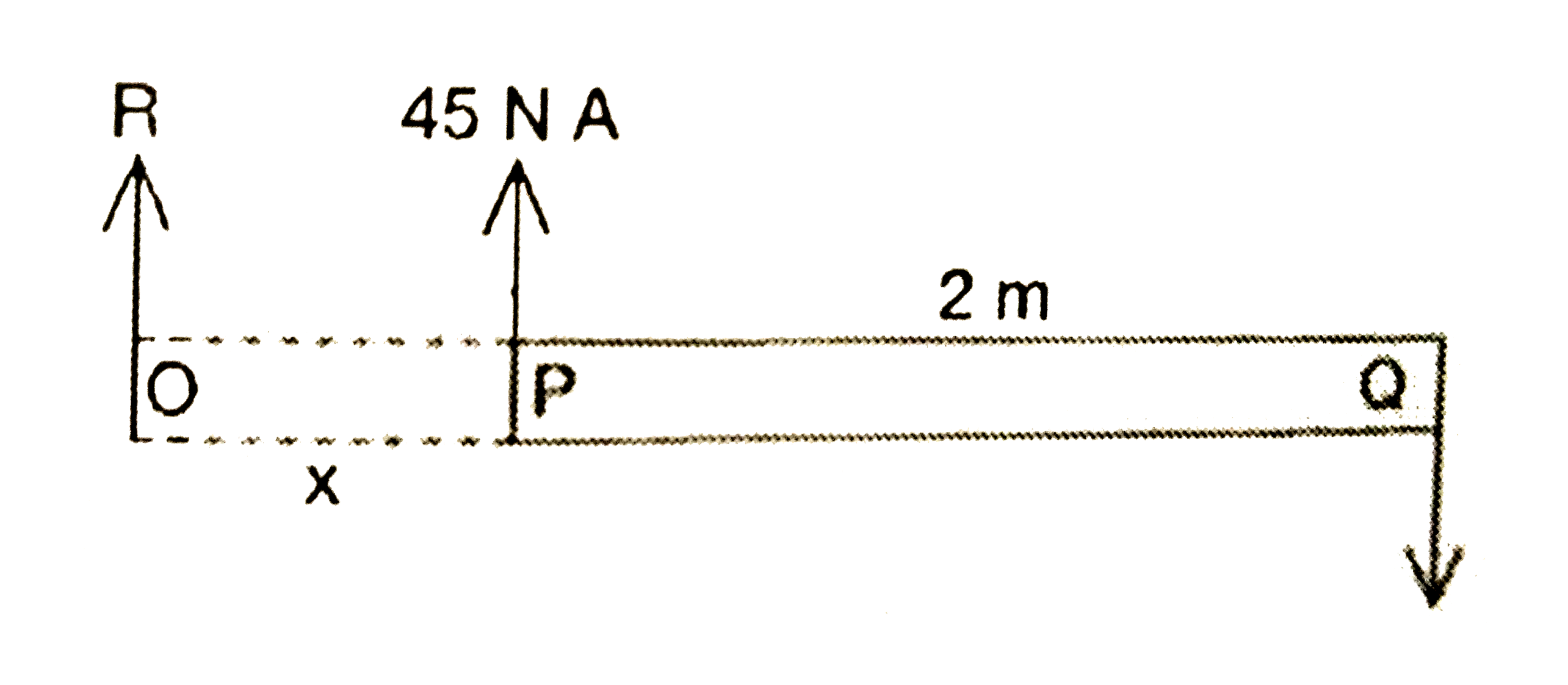
Magnitude of R = 45 - 15 = 30 N
Position of R: Let 'R' is at 'O' and at a distance of x m from 'P'. Then
$45 \times x = 15 \times (2 + x)$
$3 x = 2 + x$
$2 x = 2$
$x = 1 m$

Updated on:21/07/2023

|

Class 9 PHYSICS SIMPLE MACHINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

There are four forces acting on a block as shown in the figure. The magnitude and direction of the net force acting on it is __________.

A150 N, towards right
B100 N, upwards
C70 N, towards right
D70 N, towards left
A rod of length L and mass M is acted on by two unequal forces $F_{1}$ and $F_{2} (< F)$ as shown in the figure.

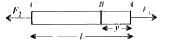
The tension in the rod at a distance y from the end A is given by
A $F_{1} (1 - \frac{y}{L}) + F_{2} (\frac{y}{L})$
B $F_{2} (1 - \frac{y}{L}) + F_{1} (\frac{Y}{L})$
C $(F_{1} - F_{2}) \frac{y}{L}$
DNone of these
Two forces $F_{1} and F_{2}$ are acting on a rod abc as shown in figure.

Aif $F_{1} = F_{2}$ then $τ_{a} = τ_{b} = τ_{c}$ ( for both forces)
Bif $F_{1} = F_{2}$ then $τ_{a} = τ_{c} \neq τ_{b}$ ( for both forces)
Cif $F_{1} \neq F_{2}$ then $τ_{a} \neq τ_{b} \neq τ_{c}$ ( for both forces)
Dif $F_{1} \neq F_{2}$ then $τ_{a} = τ_{c} \neq τ_{b}$ ( for both forces)

PEARSON IIT JEE FOUNDATION-SIMPLE MACHINES-Level- 2

Home
Ask Doubt
Profile