A uniform meter scale balances at the 40 cm mark when weights of 10g and 20g are suspended from the 10cm and 20cm marks. The weight of the metre scale is
50 g
60 g
70 g
80 g
The correct Answer is:C
To solve the problem, we will use the concept of torque and balance of moments. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a uniform meter scale that balances at the 40 cm mark. We are given two weights: 10 g suspended at the 10 cm mark and 20 g suspended at the 20 cm mark. We need to find the weight of the meter scale.
Step 2: Identify the Forces and Their Distances
- The weight of the scale (W) acts at its center of mass, which is at the 50 cm mark (since it is uniform).
- The 10 g weight acts at the 10 cm mark.
- The 20 g weight acts at the 20 cm mark.
Step 3: Calculate the Distances from the Balance Point
The balance point is at the 40 cm mark. We need to find the distances from this point to where the weights are applied:
- Distance from 40 cm to 10 cm (for 10 g): 40−10=30 cm (clockwise)
- Distance from 40 cm to 20 cm (for 20 g): 40−20=20 cm (clockwise)
- Distance from 40 cm to 50 cm (for W): 50−40=10 cm (anticlockwise)
Step 4: Set Up the Torque Equation
For the system to be in balance, the total clockwise torque must equal the total anticlockwise torque.
The torque due to the weights is:
- For the 10 g weight: 10g×30cm
- For the 20 g weight: 20g×20cm
The torque due to the weight of the meter scale (W) is:
- For the scale: W×10cm
Setting up the equation:
10g×30cm+20g×20cm=W×10cm
Step 5: Substitute and Simplify
Calculating the left side:
10×30=300g cm
20×20=400g cm
Adding these gives:
300+400=700g cm
Now, substituting back into the torque equation:
700=W×10
Step 6: Solve for W
To find W, divide both sides by 10:
W=70010=70g
Final Answer
The weight of the meter scale is 70 g.
---
We have a uniform meter scale that balances at the 40 cm mark. We are given two weights: 10 g suspended at the 10 cm mark and 20 g suspended at the 20 cm mark. We need to find the weight of the meter scale.
- The weight of the scale (W) acts at its center of mass, which is at the 50 cm mark (since it is uniform).
- The 10 g weight acts at the 10 cm mark.
- The 20 g weight acts at the 20 cm mark.
The balance point is at the 40 cm mark. We need to find the distances from this point to where the weights are applied:
- Distance from 40 cm to 10 cm (for 10 g): 40−10=30 cm (clockwise)
- Distance from 40 cm to 20 cm (for 20 g): 40−20=20 cm (clockwise)
- Distance from 40 cm to 50 cm (for W): 50−40=10 cm (anticlockwise)
For the system to be in balance, the total clockwise torque must equal the total anticlockwise torque.
- For the 10 g weight: 10g×30cm
- For the 20 g weight: 20g×20cm
- For the scale: W×10cm
10g×30cm+20g×20cm=W×10cm
Calculating the left side:
10×30=300g cm
20×20=400g cm
Adding these gives:
300+400=700g cm
700=W×10
To find W, divide both sides by 10:
W=70010=70g
The weight of the meter scale is 70 g.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on moment of inertia)
33 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A meter stick is hung from two spring balances A and B of equal lengths that are located at the 20 cm and 70 cm marks of the meter stick. Weights of 2.0N are placed at the 10cm and 40cm marks, while a weight of 1.0N is placed at the 90cm mark. The weight of the uniform meter stick is 1.5 N. Determine the scale readings of the two balances A and B.
View SolutionTo balance a uniform metre scale suspended at 50 cm mark, a with 200 g weight suspended from it at 20 cm mark, a weight of _________ g must be suspended at 90 cm mark.
View Solution
Knowledge Check
A uniform meter scale balance s at the 40-cm mark when weihgt of 10g and 20g are suspended from the 10-cm and 20-cm marks respectively. The weight of the meter scale is
A50gB60gC70gD80gAn uniform metre scale of weight 50g is balanced at 60cm mark, when a weight of 15g is suspended at 10cm mark. Where must a weight 100g be suspended to balance metre scale.
A72.5cmB70cmC71.5cmD74.5cmA uniform metre scale is balanced horizontally on a knife edge at a distance of 10 cm from its centre of gravity, when masses of 50 gm and 30 g are suspended from the 5 cm and 90 cm marks of the rod. What is the weight of the rod?
A20 gram weightB25 gram weightC40 gram weightD10 gram weight
A uniform meter scale is kept in equilibrium when supported at the 60 cm mark and a mass weight of the scale is greater than, less than or equal to the weight of mass M.
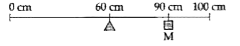
View SolutionA uniform metre scale of weight 20 gf is supported on a wedge placed at 60 cm mark. If a weight of 30 gf is suspended at 15 cm mark, where should a weight 200 gf be suspended in order to balance the metre scale?
View SolutionA metre scale is supported on a wedge at its centre of gravity. A body of weight w is suspended from the 15 cm mark and another weight of 30 gram suspended from 71 cm mark balances it the metre scale remains perfectly horizontal. What is the weight of the body? Neglect the weight of the centre scale.
View SolutionA meter scale is balanced at its mid point if a 20N weight is balanced at 20 cm mark and a 30 N weight hanged at x cm mark. Calculate the value of x.
View SolutionA uniform thermometre scale is at steady state with its 0 cm mark at 20°C and 100 cm mark at 100°C. Temperature of the 60 cm mark is-
View Solution
