A uniform metre rod is balanced at the 70 cm mark by suspending a weight of 50 gf at the 40 cm mark and 200 gf at the 95 cm mark. Draw a diagram of the arrangement and calculate the weight of the metre rod.
Step-by-Step Solution:
1. Understanding the Problem:
We have a uniform meter rod that is balanced at the 70 cm mark. We need to find the weight of the rod (W) given two weights: 50 gf at the 40 cm mark and 200 gf at the 95 cm mark.
2. Drawing the Diagram:
- Draw a horizontal line to represent the meter rod.
- Mark the 0 cm to 100 cm scale on the rod.
- Indicate the 70 cm mark as the balance point.
- Place a weight of 50 gf at the 40 cm mark and a weight of 200 gf at the 95 cm mark.
3. Applying the Principle of Moments:
The principle of moments states that for an object to be in equilibrium, the clockwise moments about a pivot must equal the anti-clockwise moments.
- Clockwise Moments:
- The moment due to the 200 gf weight at the 95 cm mark:
Moment=Force×Distance from pivot=200gf×(95−70)cm=200×25gf cm
- Anti-clockwise Moments:
- The moment due to the 50 gf weight at the 40 cm mark:
Moment=50gf×(70−40)cm=50×30gf cm
- The moment due to the weight of the rod (W) acting at its center, which is at the 50 cm mark:
Moment=W×(70−50)cm=W×20gf cm
4. Setting Up the Equation:
Since the clockwise moments equal the anti-clockwise moments, we can write:
200×25=50×30+W×20
5. Solving for W:
- Calculate the left side:
200×25=5000gf cm
- Calculate the right side:
50×30=1500gf cm
- Substitute these values into the equation:
5000=1500+W×20
- Rearranging gives:
W×20=5000−1500=3500
- Now, divide by 20 to find W:
W=350020=175gf
6. Conclusion:
The weight of the meter rod is 175 gf.
We have a uniform meter rod that is balanced at the 70 cm mark. We need to find the weight of the rod (W) given two weights: 50 gf at the 40 cm mark and 200 gf at the 95 cm mark.
- Draw a horizontal line to represent the meter rod.
- Mark the 0 cm to 100 cm scale on the rod.
- Indicate the 70 cm mark as the balance point.
- Place a weight of 50 gf at the 40 cm mark and a weight of 200 gf at the 95 cm mark.
The principle of moments states that for an object to be in equilibrium, the clockwise moments about a pivot must equal the anti-clockwise moments.
- The moment due to the 200 gf weight at the 95 cm mark:
Moment=Force×Distance from pivot=200gf×(95−70)cm=200×25gf cm
- The moment due to the 50 gf weight at the 40 cm mark:
Moment=50gf×(70−40)cm=50×30gf cm
- The moment due to the weight of the rod (W) acting at its center, which is at the 50 cm mark:
Moment=W×(70−50)cm=W×20gf cm
Since the clockwise moments equal the anti-clockwise moments, we can write:
200×25=50×30+W×20
- Calculate the left side:
200×25=5000gf cm
- Calculate the right side:
50×30=1500gf cm
- Substitute these values into the equation:
5000=1500+W×20
- Rearranging gives:
W×20=5000−1500=3500
- Now, divide by 20 to find W:
W=350020=175gf
The weight of the meter rod is 175 gf.
Topper's Solved these Questions
Similar Questions
A uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Draw a diagram of the arrangement.
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View Solution
Knowledge Check
Find the weight of half meter scale balanced at 5 cm mark when a weight of 10 gf is suspended at one of its ends.
A2.5gfB100gfC0.2gfD50gf
A uniform metre rule between horizontally on a knife edge placed at the 58cm mark when a weight of 20gf is suspended from one end.
(i) Draw a diagram of the arrangement.
(ii) What is the weight of the rule?
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
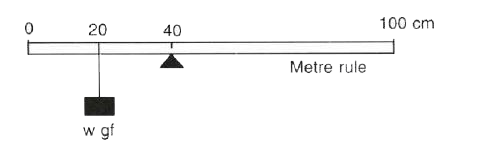
the resultant moment and its direction if the weight w is moved to the mark 30 cm.
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
View SolutionA uniform half metre rule can be balanced at the 29.0cm mark when a mass 20g is hung from its one end.
(a) Draw a diagram of the arrangement
(b) Find the mass of the half metre rule.
( c) In Which direction would the balancing point shift if 20g mass is shifted inside from its one end?
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
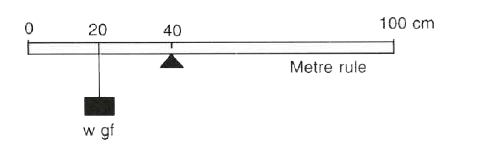
the position of another weight of 50 gf to balance the rule in part (ii).
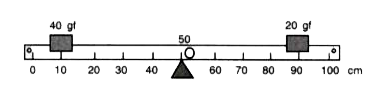
View SolutionFig.1.33 shows a uniform metre rule placed on a fulcrum at its mid point O and having a weight 40gf at the 10cm mark and a weight of 20gf at the 90cm mark. (i) Is the metre rule in equilibrium? If not , how will the turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?
View SolutionA uniform thermometre scale is at steady state with its 0 cm mark at 20°C and 100 cm mark at 100°C. Temperature of the 60 cm mark is-
View Solution
