A uniform plane sheet of metal in the form of a triangle has . Its moment of inertia will be smallest
about as axis
about as axis
about as axis
with a line through normal to its plane as axis,
The correct Answer is:C
Distribution of mass nearest in option c.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤ADFigure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
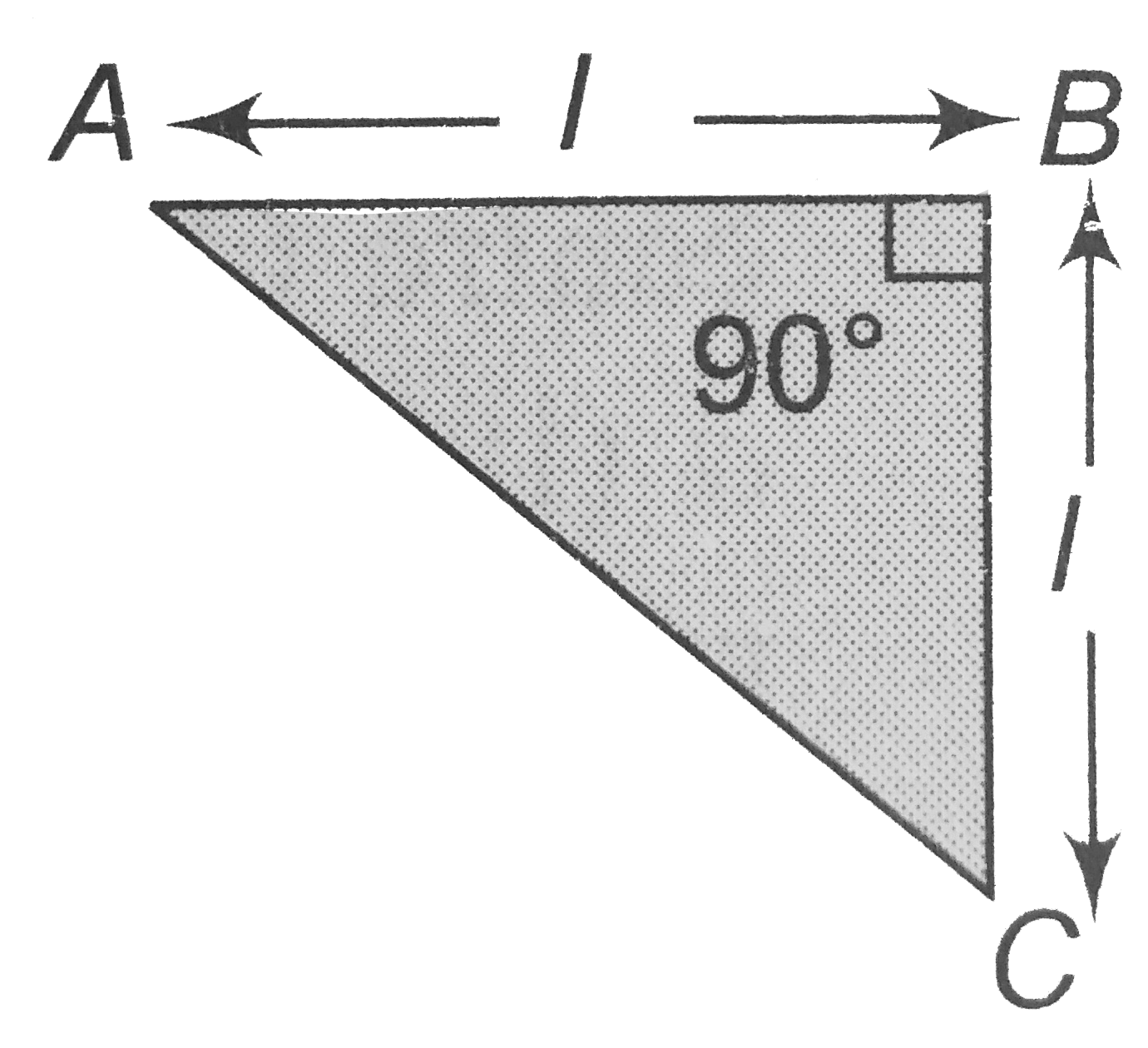 .AMl218BMl212CMl26DMl24
.AMl218BMl212CMl26DMl24The ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB,IBC and lCA are the moments of inertia of the plate about AB, BC and CA respectively. Which one of the following relation is correct?
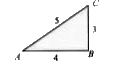 AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IAB
AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IAB
If D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionIn the figure, show that 2(AC+BD)>AB+BC+CD+DA.

View SolutionABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct?
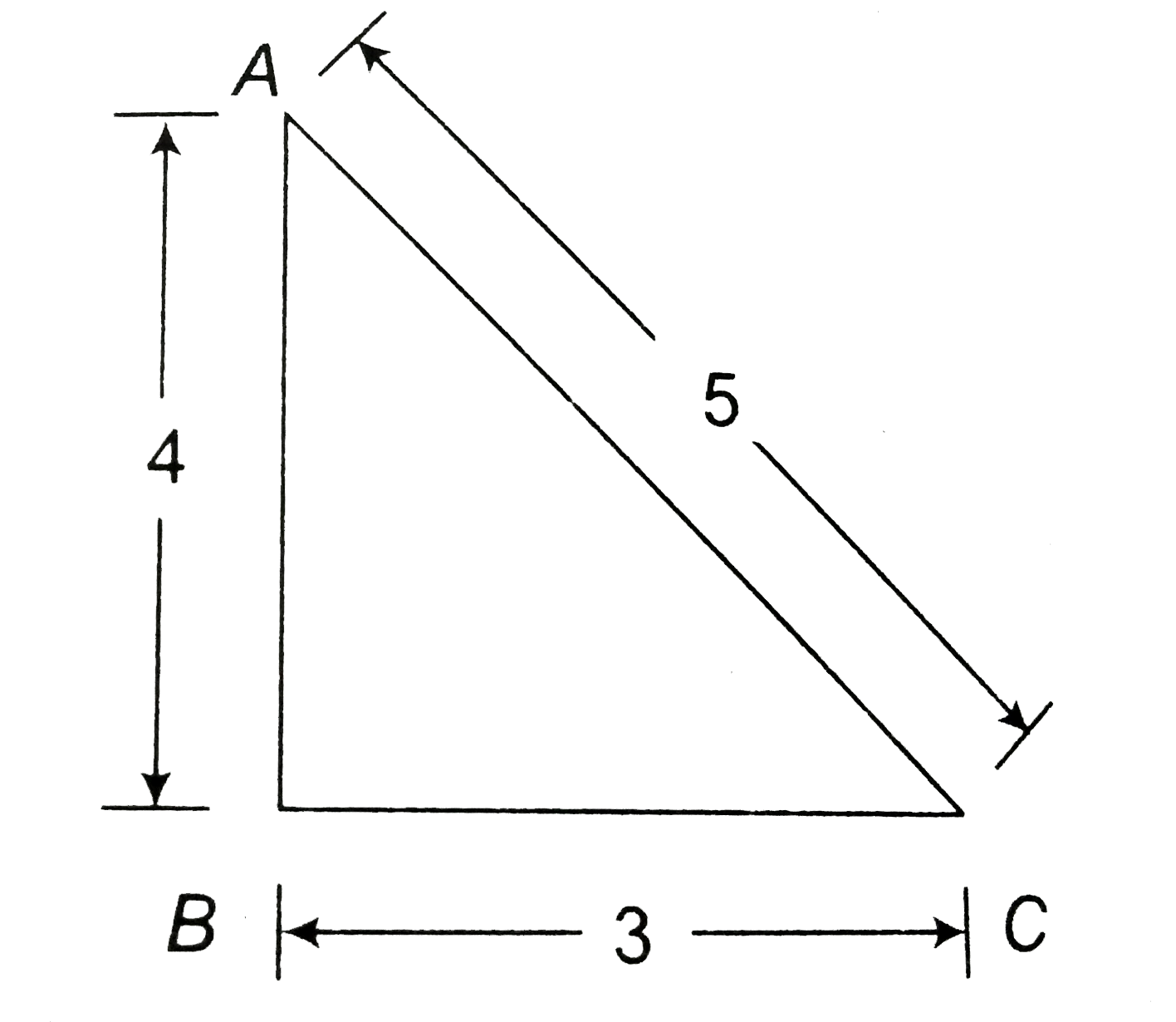
View SolutionIn two triangle ABC and DEF, AB= DE ,BC=DF and AC =Ef then
View SolutionABC is a triangular plate of uniform A thickness. The sides are in the ratio shown in the figure. IAB,IBC,ICA are the moments of inertia of the plated about AB,BC and CA respectively. Which one of the following relation is correct?
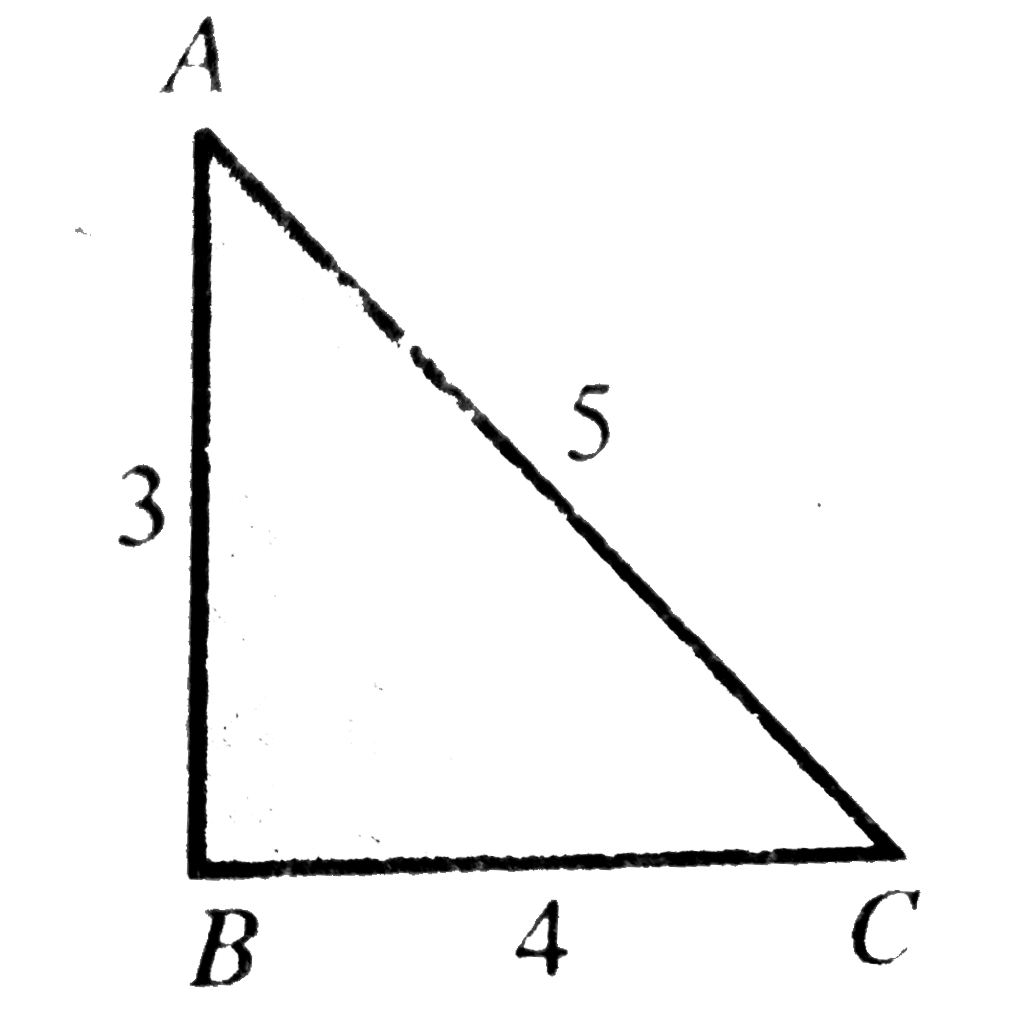
View Solution

