A uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
At O
At a distance less than //2 from O
At a distance HI from O
At a distance larger than//2from
The correct Answer is:C
Step by step video, text & image solution for A uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Numerical MCQs Single Option Corrrect
39 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - paragraph
24 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
Similar Questions
A uniform rod of length l is kept vertically on a rough horizontal surface at x = 0 . It is rotated slightly and released . When the rod finally falls on the horizontal surface , the lower end will remain at

View SolutionA uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre :
View Solution
Knowledge Check
A particle, moving horizontally, collides perpendicularly at one end of a rod having equal mass and placed on a smooth horizontal surface.
 AParticle comes to rest if collision is perfectly elastic and centre of m rod starts to move with the same velocity.BParticle continues to move along the same direction, whatever is the value of e.CParticle may get rebound back.DVelocity of mid-point of the rod will be less than v/2 if the particle gets stuck.
AParticle comes to rest if collision is perfectly elastic and centre of m rod starts to move with the same velocity.BParticle continues to move along the same direction, whatever is the value of e.CParticle may get rebound back.DVelocity of mid-point of the rod will be less than v/2 if the particle gets stuck.A rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be
 Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]
Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]A uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
AhorizontallyBvertically downCin a parabolic pathDdoes not move
A uniform sphere is place on a smooth horizontal surface and as horizontal force F is appied on it at a distance h above the surface. The acceleratioin of the centre
View SolutionA uniform rod of mass m and length l is kept vertical with the lower end clamped. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest position. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?
View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA uniform rod ABC of mass M is placed vertically on a rough horizontal surface. The coefficient of kinetic friction between the rod and the surface is μ.A force F (>μmg) is applied on the rod at point B at distance l/3 below centre of the rod as shown in figure. The initial acceleration of point A is
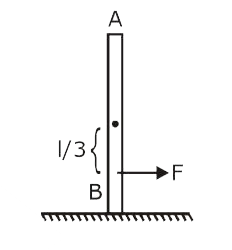
View SolutionA uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View Solution
