
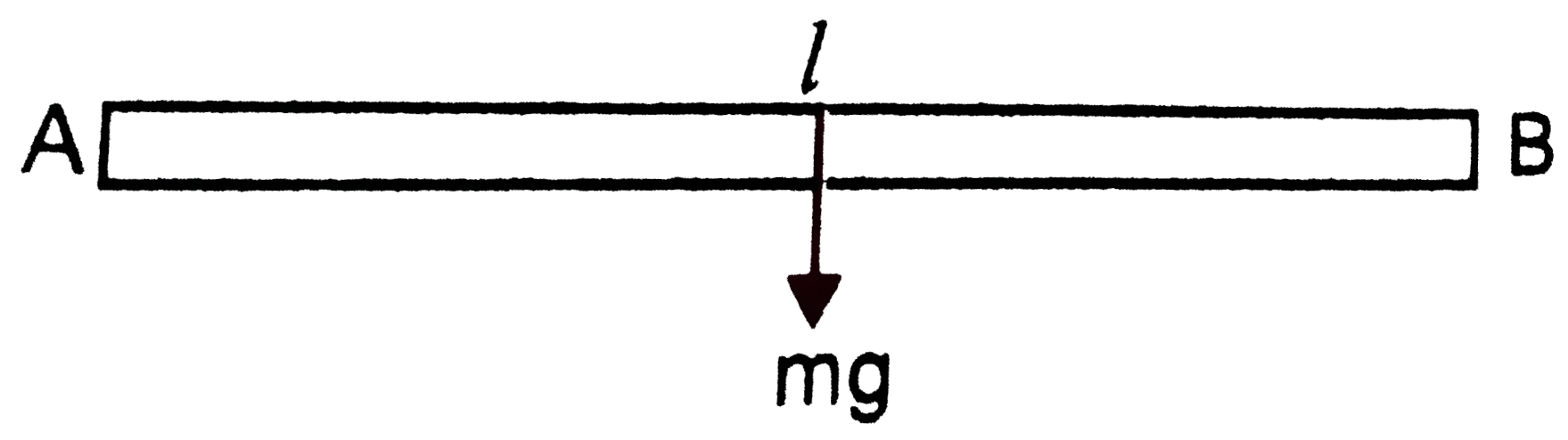
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
3mg2
2mg
zero
mg2
The correct Answer is:C

α=τnetI
=⎛⎜
⎜⎝mg(l2)+mglml2/3⎞⎟
⎟⎠
=4.5gl
acoin=lα=4.5g
mg−N=macoin
∴N=mg−macoin=−3.5g

Since, N can't be negative.
So, N=0 and coin can not remain in contact with rod.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View Solution
Knowledge Check
A unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2glA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
 A2g3lBmgl2C32glD3g2l
A2g3lBmgl2C32glD3g2lA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
 A2g3lBmgl2C32glD3g2l
A2g3lBmgl2C32glD3g2l
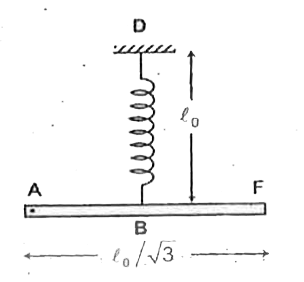
In the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml2/3, the initial angular acceleration of the rod will be
View SolutionTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.

View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
View Solution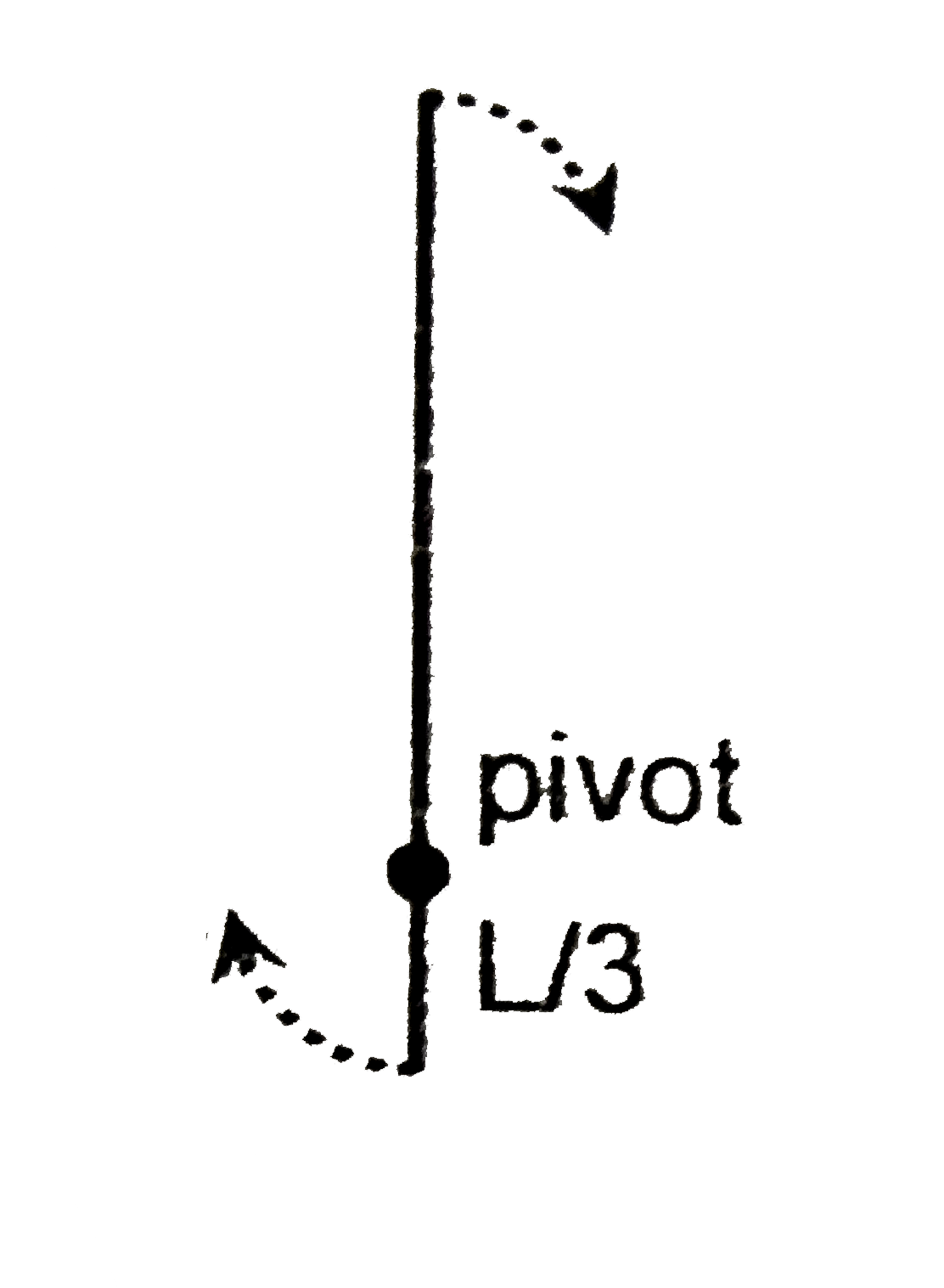
A uniform rod of mass M and length L is free to rotate about a frictionless pivot located L/3 from one end. The rod is released from rest incrementally away from being perfectly vertical, resulting in the rod rotating clockwise about the pivot. when the rod is horzontal what is the magnitude of the tangential acceleration of its center of mass?
View Solution
