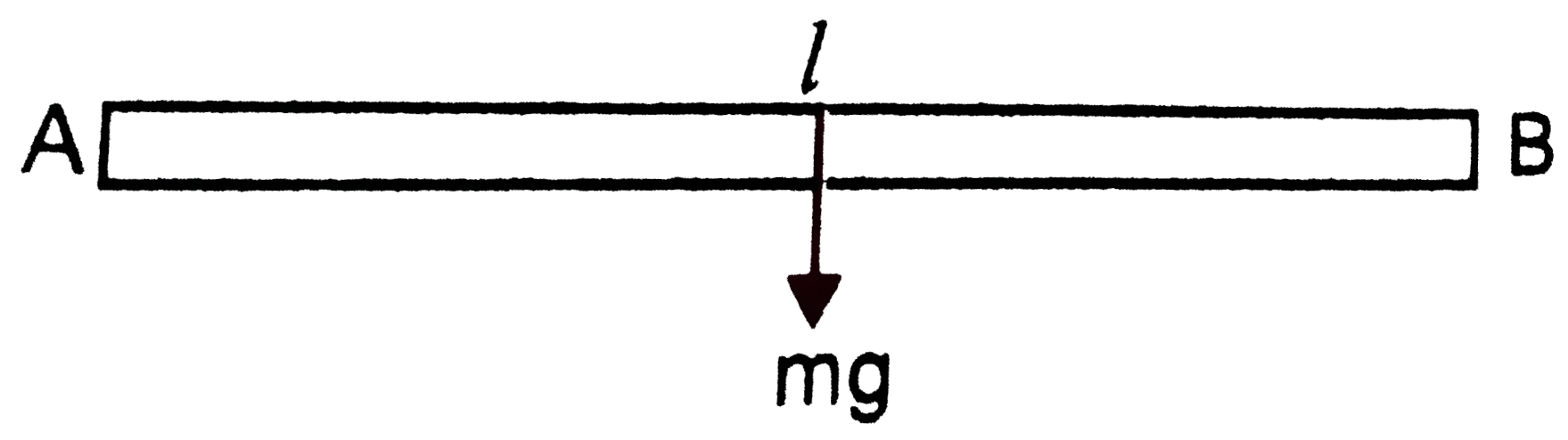
A uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
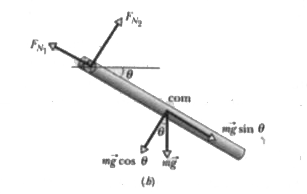
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
(1) It is easy to imagine that rod rotates clockwise around the pivot at the left end, when it is released. The rod will be experiencing two forces, one is the weight, effectively acting on center of mass and the other is the force due to hinge or pivot, acting through the hinge. (2) When we write torque about the pivot the torque due to second force will become zero because its moment arm is zero. Now the torque is due to only the gravitational force on the rod. For the rotation axis considered crossing the pivot, the rod is a rigid body under a net torque.
Calculation: We know the gravitational force acts effectively at the center of mass of the rod as shown in Fig.
The magnitude of the torque due to the weight about an axis through the pivot,
τ=Mg(l2)
Using Eq. to obtain the angular acceleration of the rod,
α=τI=Mg(l2)13Ml2=3g2l
(b) Compute: Using Eq. with r = l for the initial acceleration of the right end of the rod, we get
αi=lα=32g
( c) Calculations: We know the gravitational force effectively acts at the center of mass of the rod as shown in Fig. The magnitude of the torque due to the weight about an axis through the pivot is given by
mgcosθ×l2=ml23×α
α=3gcosθ2l
By energy conservation,
mg12sinθ=12ml23ω2
ω=√3gsinθl
ar=ω2l2=3gsinθl×l2=3gsinθ2
at=α12=3gcosθ4
FN1−mgsinθ=m3gsinθ2
FN1=5mgsinθ2
mgcosθ−FN2=m3gcosθ2
FN2=mgcosθ4
FN=√FN21+FN22
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
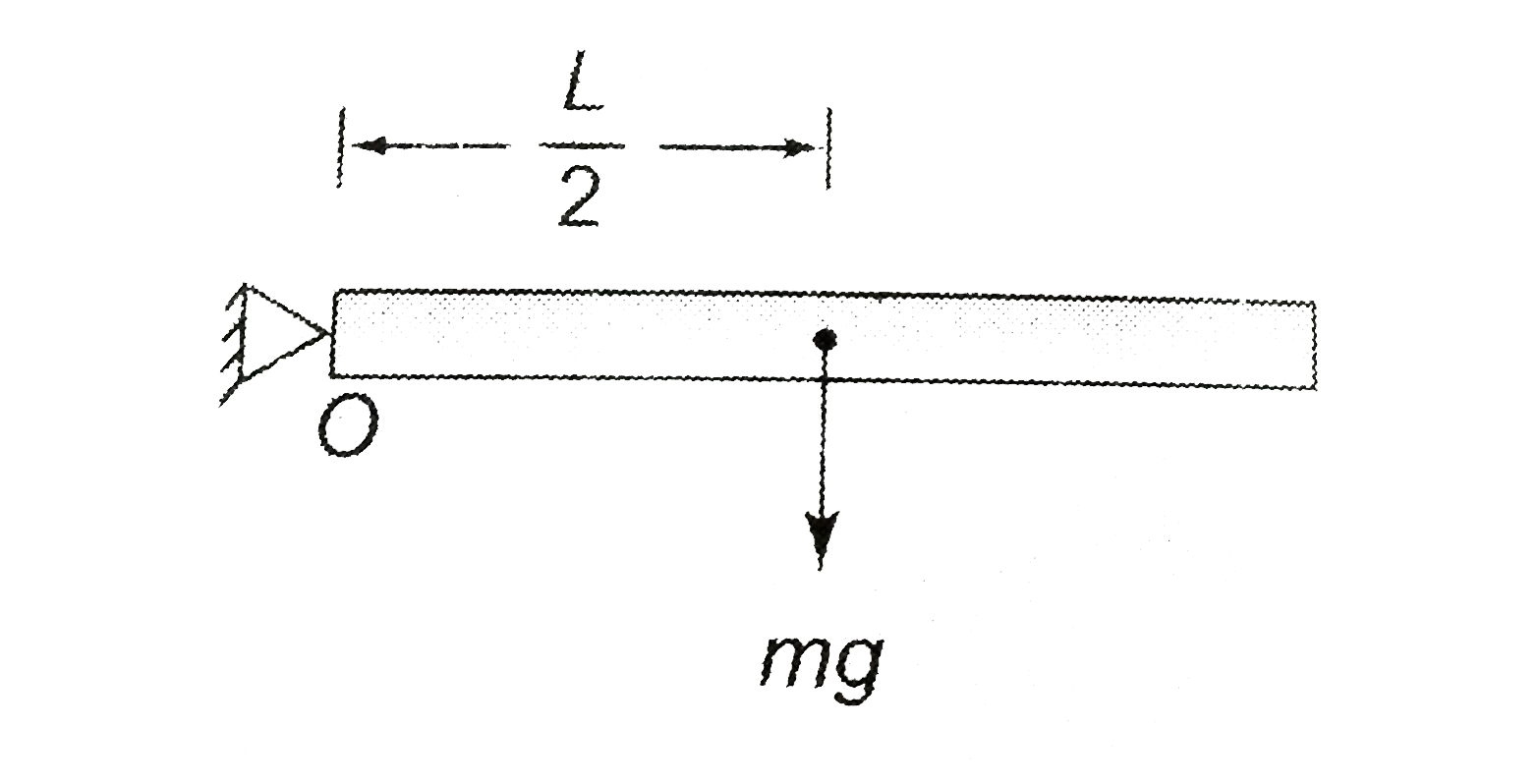
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View Solution
Knowledge Check
A unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2glA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15A uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml2/3, the initial angular acceleration of the rod will be
 Amgl2B32glC3g2lD2g3l
Amgl2B32glC3g2lD2g3l
A uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)

View Solution
