A uniform rod of mas m is moving with constant velocity v0 in a perpendicular uniform magnetic field B as shown. The resistance of rod is r . The current flowing through rod, RI and R2 will be 
The rod can be replaced by a battery of emf e=Bv0L and internal resistance r .
3r and 6r in parallel, Req'=3r.6r3r+6r=2r
i=Bv0Lr+2r=Bv0L3r
VA−VB=i.2r=2Bv0L3
i=2Bv0L/36r=2Bv0L9r
i2=2Bv0L/36r=Bv0L9r
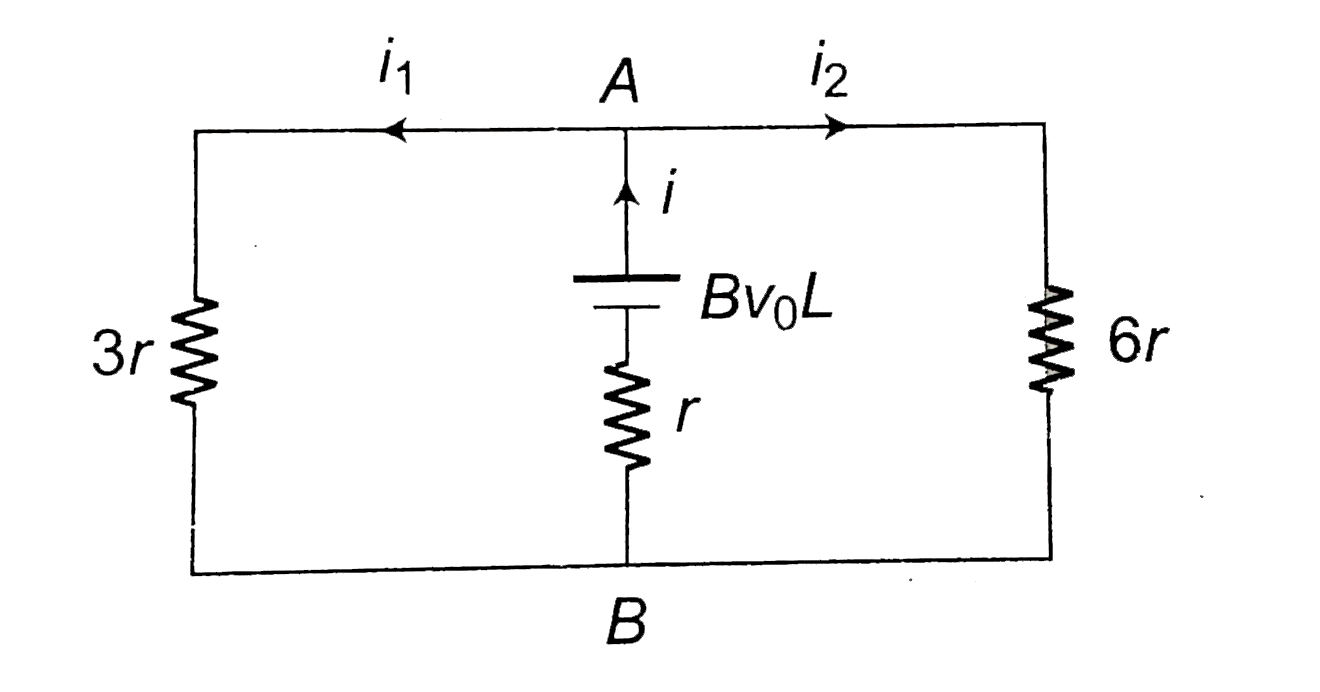

Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure.
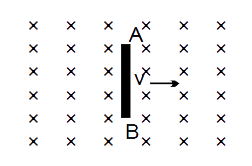 AThe rod becomes electrically chargedBThe end A becomes positively chargedCThe end B becomes positively chargedDThe rod becomes hot because of Joule heating
AThe rod becomes electrically chargedBThe end A becomes positively chargedCThe end B becomes positively chargedDThe rod becomes hot because of Joule heating - Question 2 - Select One
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2R - Question 3 - Select One
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
 AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
A metal rod of length I is moved with velocity v in a uniform magnetic field →B. Emf is induced between the two ends of rod
View SolutionA metal rod of length 2m is rotating with an angular velocity of 100rad/sec in a plane perpendicular to a uniform magnetic field of 0.3T. The potential difference between the ends of the rod is
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View SolutionA conducting rod of length l is falling with a velocity v perpendicular to a uniform horizontal magnetic field B. The potential difference between the two ends will be
View SolutionAB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R1 and R2 do not rotate. Then the current through the resistor R1 is
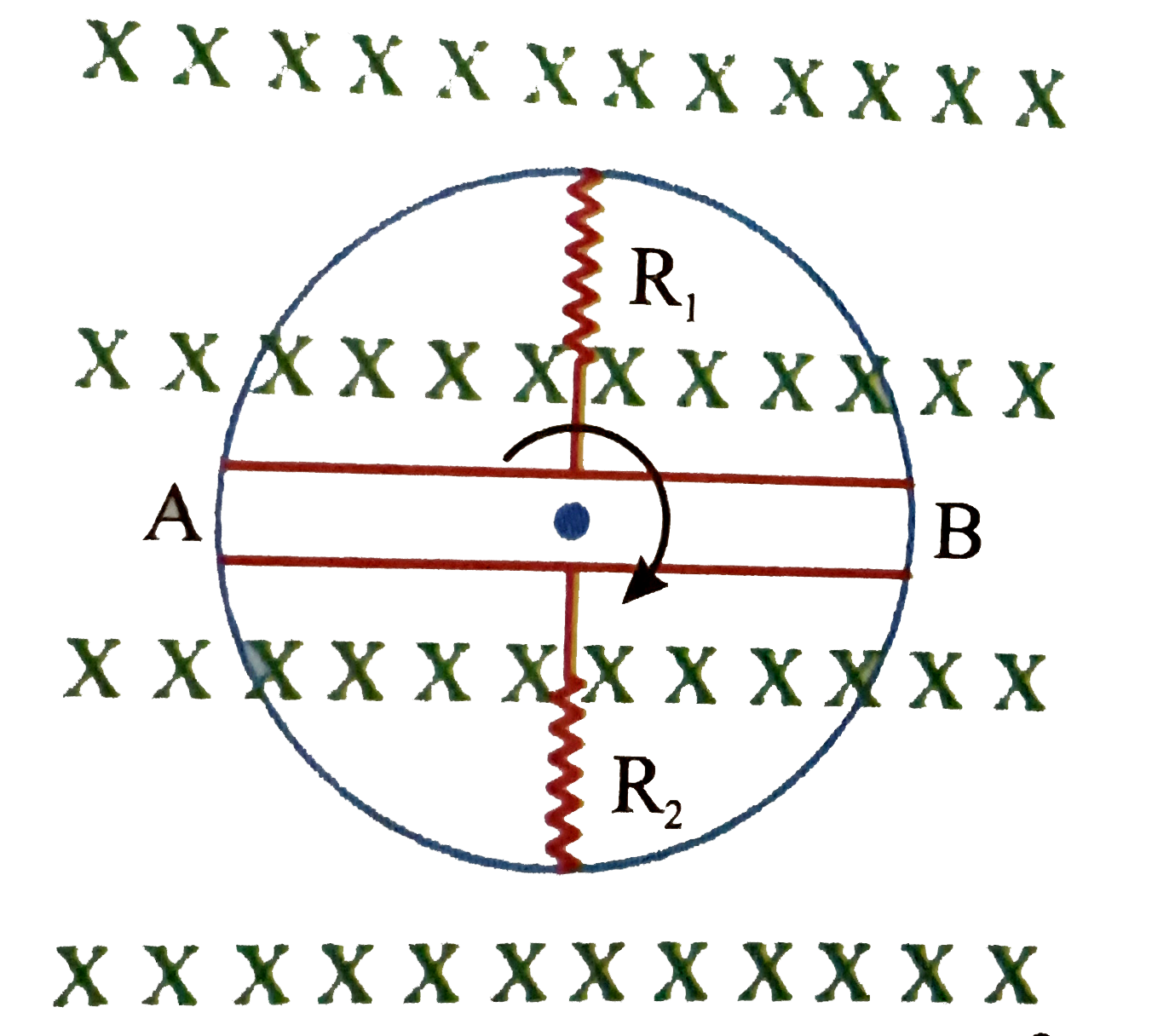 View Solution
View Solution

