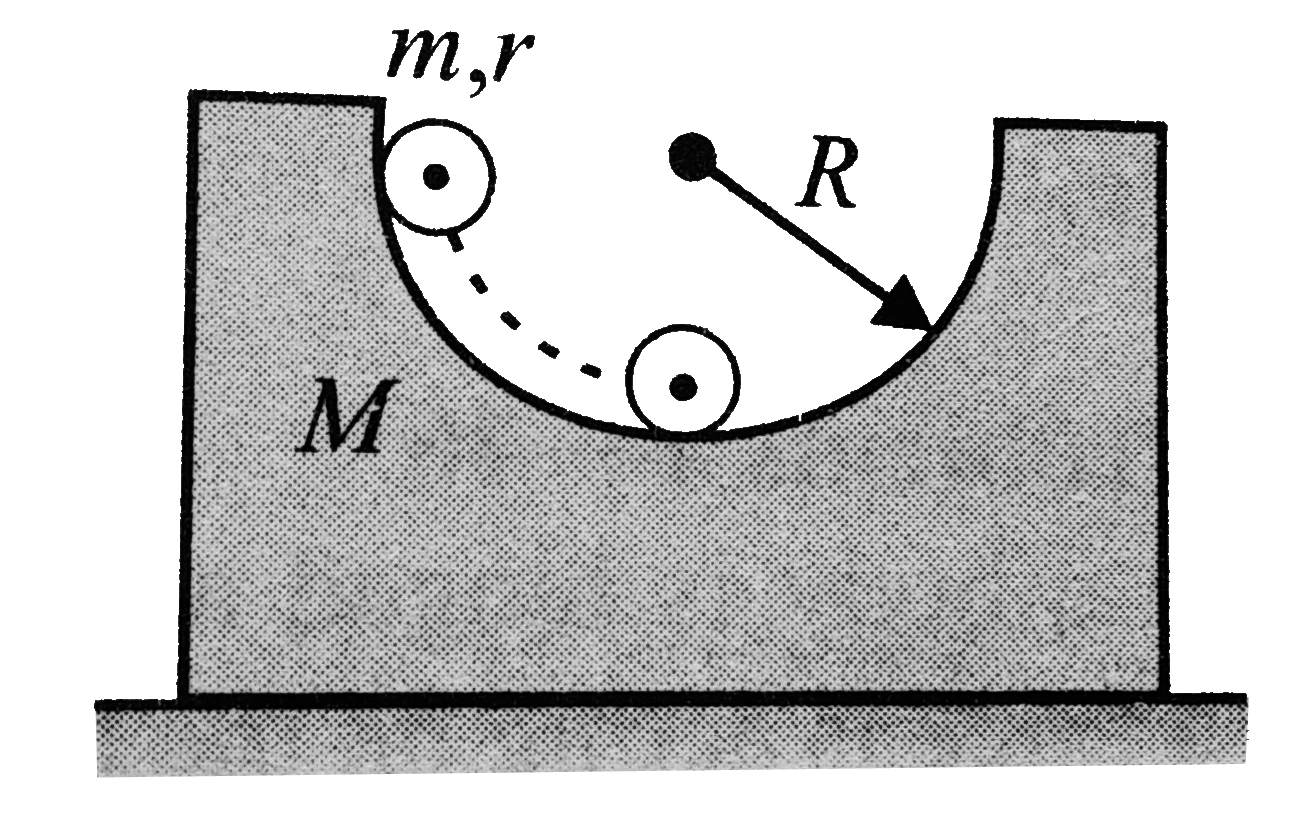
A uniform solid cylinder of mass and radius is released from rest at the top of a semicircular track of radius cut in a block of mass as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is
The correct Answer is:D
As no external force acting force is acting on the system (block cylinder) in the horizontal direction, the linear momentm of the system remains conserved in the horizontal direction.
As the cylinder reachs the bottommost point of the track, its centre of mass covers a horizontal distance of w.r.t block towards the right. Let the block move by in backward direction then

Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ?
View Solution
Knowledge Check
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
The speed of the cylinder when it reaches the bottom of the track isA2√11m/sB8√11m/sC8√11m/sD6√11m/sA uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
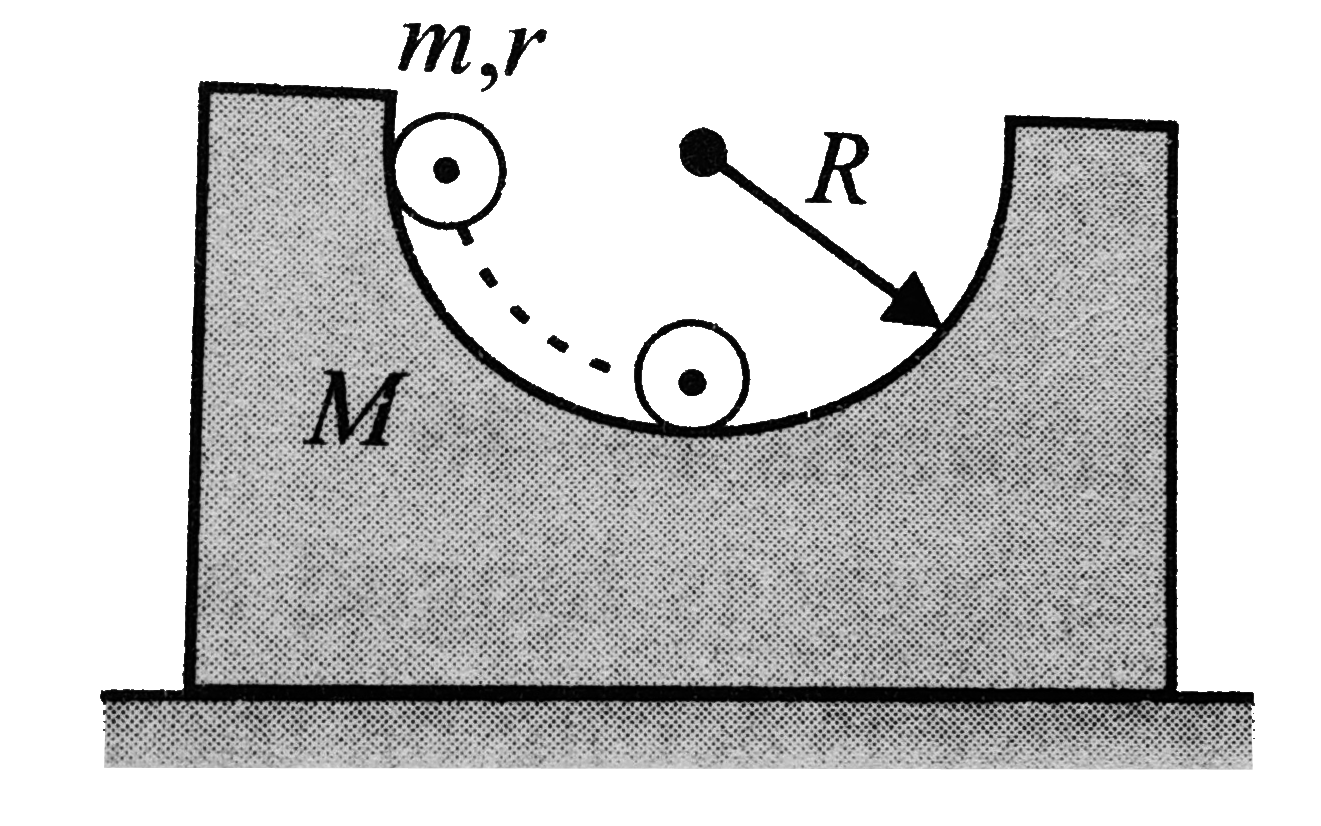
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track isA2√11m/sB8√11m/sC4√11m/sD6√11m/sA solid cylinder of mass 1 kg and radius 0.02 m, is rolling on a smooth horizontal surface with a uniform velocity of 0.1 m/s. Its total energy is
A7.5×10−3JB7.5×10−2JC7.5×10−4JD7.5×10−6J
A solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
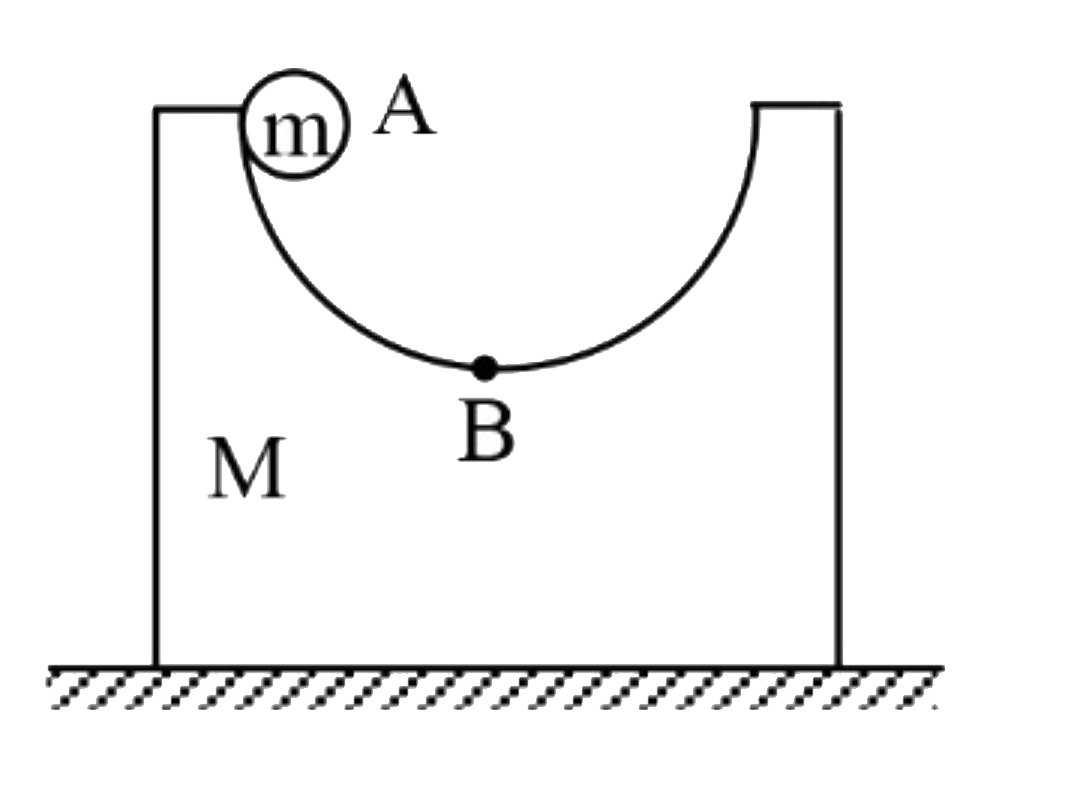
View SolutionA block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g=10ms−2)
View Solution
