A uniform sphere of radius a rotating with an angular velocity ω about an axis perpendicualr to the plane of motion and its cener impinges on a horizontal plane, let u and v are horizontal and vertical component of velocity before impact. Then
if u = aω, then u and ω are unaltered
if u = aω, then surface is frictionless
If ugt aω, then angular velocity increases
all of the above
To solve the problem of a uniform sphere of radius a rotating with an angular velocity ω about an axis perpendicular to the plane of motion, and its center impinging on a horizontal plane, we need to analyze the components of velocity before the impact and the implications of the conditions given.
1. Identify the Components of Velocity:
- Let u be the horizontal component of velocity before impact.
- Let v be the vertical component of velocity before impact.
2. Relate the Horizontal Velocity to Angular Velocity:
- The linear velocity u at the edge of the sphere due to its rotation can be expressed as:
u=aω
- This equation indicates that the horizontal velocity u is directly proportional to the angular velocity ω and the radius a of the sphere.
3. Consider the Nature of the Surface:
- If the surface is frictionless, the horizontal component of velocity u remains unchanged during the impact. Therefore, the horizontal velocity after impact will still be u.
4. Analyze the Conditions:
- If u=aω, then the sphere is rolling without slipping. This means that the relationship holds true, and both u and ω are unaltered.
- If u>aω, the sphere will slide on the surface, and its angular momentum will increase due to the additional translational motion.
5. Conclude the Options:
- Based on the analysis:
- If u=aω, then both u and ω are unaltered (Option A is correct).
- If the surface is frictionless, u remains constant (Option B is correct).
- If u>aω, the angular momentum L increases (Option C is also correct).
Final Answer:
All options provided in the problem are correct based on the analysis of the motion of the sphere before and after impact.
- Let u be the horizontal component of velocity before impact.
- Let v be the vertical component of velocity before impact.
- The linear velocity u at the edge of the sphere due to its rotation can be expressed as:
u=aω
- This equation indicates that the horizontal velocity u is directly proportional to the angular velocity ω and the radius a of the sphere.
- If the surface is frictionless, the horizontal component of velocity u remains unchanged during the impact. Therefore, the horizontal velocity after impact will still be u.
- If u=aω, then the sphere is rolling without slipping. This means that the relationship holds true, and both u and ω are unaltered.
- If u>aω, the sphere will slide on the surface, and its angular momentum will increase due to the additional translational motion.
- Based on the analysis:
- If u=aω, then both u and ω are unaltered (Option A is correct).
- If the surface is frictionless, u remains constant (Option B is correct).
- If u>aω, the angular momentum L increases (Option C is also correct).
All options provided in the problem are correct based on the analysis of the motion of the sphere before and after impact.
Topper's Solved these Questions
- BOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives9videos
ROTATIONAL MOTION
- BOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives23videos
NEWTONS LAWS OF MOTION AND FRICTION
- BOOK - BITSAT GUIDECHAPTER - SCALARS AND VECTORSEXERCISE - All Questions34videos
SCALARS AND VECTORS
Similar Questions
A uniform heavy disc is rotating at constant angular velocity ω about a vertical axis through its centre and perpendicular to the plane of the disc. Let L be its angular momentum. A lump of plasticine is dropped vertically on the disc and sticks to it. Which of the following will be constant?
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution
Knowledge Check
- Question 1 - Select One
A heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchanged - Question 2 - Select One
A uniform circular metal disc of radius R is rotating about a vertical axis passing through its centre and perpendicular to its plane with constant frequency f. If BH and BV are horizontal and vertical components of the Earth's magnetic field respectively, then the induced e.m.f between its centre and the rim is
AπBVfR2BπBHfR2C2πBVfR2DZero - Question 3 - Select One
A horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
AzeroBπr2ωBC12Br2ωDBr2ω
A wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
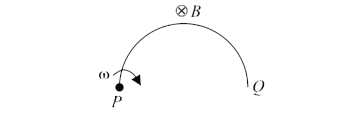 View Solution
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to the plane at an angular velocity ω . Another disc of mass M / 3 but same radius is placed gently on the first disc coaxially . the angular velocity of the system now is
View SolutionA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
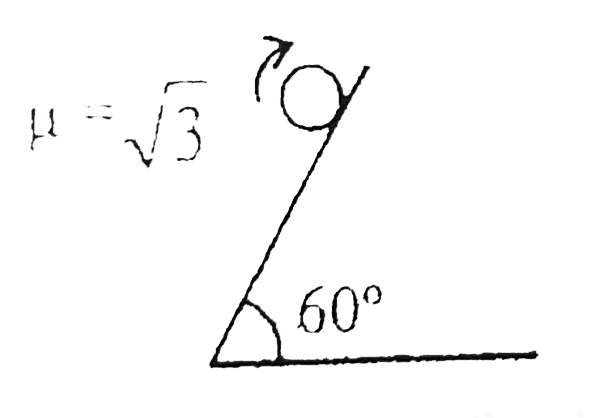 View Solution
View SolutionAn aeroplane takes off at an angle of 60∘ to the horizontal. If the velocity of the plane is 200kmh−1,calculate its horizontal and vertical component of its velocity (in kmh−1) .
View Solution

